BUAA_OO_第一单元总结

OO第一单元总结

摘要

• Homework1：本次作业，需要完成的任务为简单多项式导函数的求解。

• Homework2：本次作业，需要完成的任务为包含简单幂函数和简单正余弦函数的导函数的求解。

• Homework3：本次作业，需要完成的任务为包含简单幂函数和简单正余弦函数及其嵌套组合函数的导函数的求解。

第一次作业

第一次作业是简单多项式求导，很容易得出多项式 -> 项 -> 因子的思路，由上而下解析完输入，就可以比较快速地完成求导，并且由于因子的简单性，加上事前的了解以及实验课的帮助，很自然地想到使用HashMap进行多项式的存储和项的合并化简。感谢群里问可不可以使用实验课代码的同学的启发。

我的构造策略如下：

• 因为本次没有WF的处理，所以对输入进行预处理，去除空格和\t，将连续的两个加减号（共四种组合）进行合并，得到比较简洁的表达式。

• 利用split和正则表达式结合，匹配到连接各项的加减号之前的位置，进行分割，存入字符串数组。（此时还对java使用不够熟练，所以没有使用更便利的容器）。

• 构造Poly类，有coe和exp两个属性，并配置了简单的求导方法。

• 在MainClass中设计了cal方法，传入一项，根据正则表达式匹配出因子（常数因子、变量因子），并将该因子求导后直接存入PolyMap中的HashMap，在存入过程中根据实验课的思路直接完成相等指数的合并和系数为0的项的删去。

• 重写PolyMap的toString方法，输出结果多项式。

• 本次作业UML图及主要类

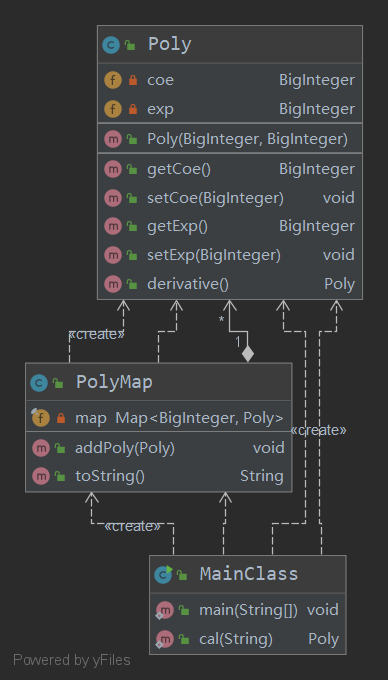
度量分析

 

 

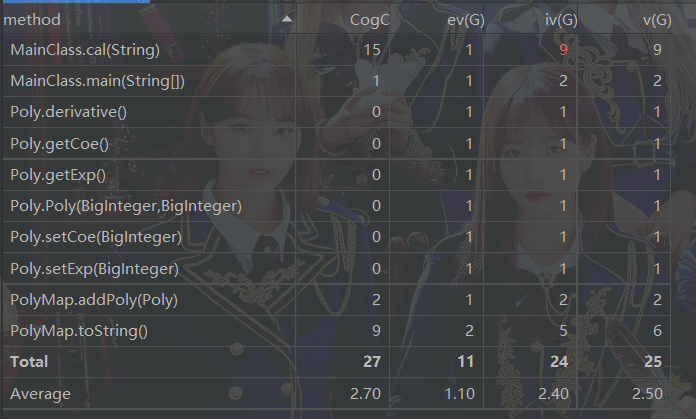
从度量分析图中可以看出，MainClass中的cal方法的模块设计复杂度偏高，反思后发现这个类起到提取并返回因子的作用，基本上是按照面向过程的思想设计的，且有比较复杂的if-else的嵌套，耦合度较高。其他各类基本上分工明确。

Bug分析

本次作业在强测和互测中没有出现Bug，且由于因子比较简单，性能分可以比较轻松地争取。

Hack环节我所在房间的同学的bug主要集中在三连符号的处理失误。

优缺点分析

优点：比较简洁直观地解决了问题，且初步尝试了按照面向对象的思想进行了相关的设计。

缺点：没有思考相关拓展的实现，只关注了第一次作业本身，导致第一次作业虽然写得很爽但是第二次极度难受。

第二次作业

第二次作业加入了三角函数因子和表达式因子，递归嵌套意味着我第一次作业使用的项分割方法、因子提取方法，以及化简方法，全部无法复用。

重构经历

开始重构之后，思考指导书中提倡的表达式树也是久久没有进展，从开始到挣扎到放弃，一直拖到星期六下午。然后午休之后一个hxd突然敲门来讨论思路，两个人基情讨论一小时，突然想通，敲定了最后的思路。但是因为没有合适的方案，加上完成基本功能比较晚，并未进行深度的化简。

• 新增Parse类，负责式子的预处理、项的分割、因子的分割。预处理基本上与第一次相同，但是新增了将**替换成^，以及将三角函数的小括号替换为中括号（但是这样的投机取巧为我最后的debug和强测互测带来了巨大的负面影响），项的分割和因子的分割均使用了栈的思想，来处理带有表达式因子的式子。

• 新增Factor类，PowFact、ConstFact、SinFact、CosFact、ExprFact均继承此类，并实现相应的deri和toString方法。

• 新增FactorFactory方法，应用pre中初步了解的工厂模式，结合小的正则表达式，实现因子的提取。

• 新增Derivation方法，传入一项，返回该项的求导结果。采取这种方法的原因是项中只有各个因子的相乘，传入整项可以整体处理乘法求导法则。遍历该项各个因子，调用该因子的求导方法，返回一个字符串，再使用这个这个求导结果乘其他所有因子，就完成了乘法法则的处理。

• 表达式因子的求导方法是本次的主要工作。其deri方法为将括号中的字符串当作一个新的项，进行上述的解析步骤并调用Derivation方法，返回一个带括号的字符串，相当于对Derivation方法的一个小型的递归实现。

• 主要思路是解析式子后使用一个ArrayList存储各项，然后遍历该ArrayList，对每个item调用Derivation，得出结果。

• 本次作业UML图

 

 

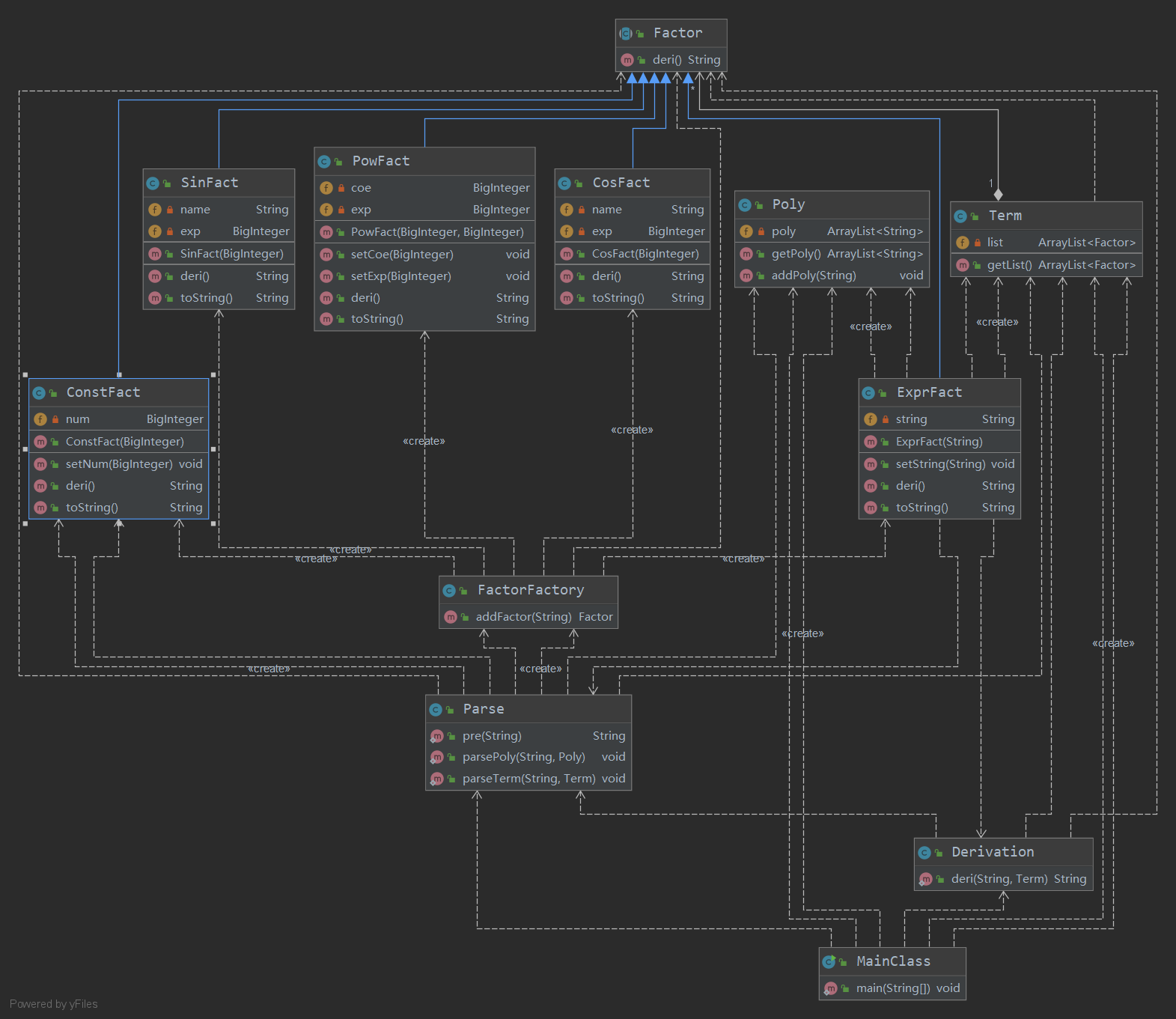
度量分析

 

 

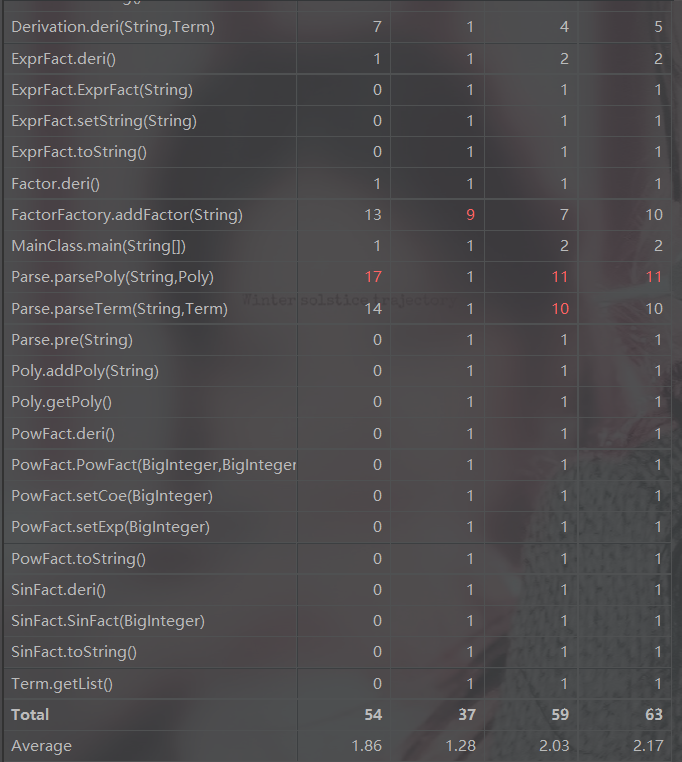
本次作业设计的复杂之处主要集中在工厂模式的不合理使用以及对式子的解析。工厂模式中通过正则表达式来匹配因子，其实是比较冗余的，引入了很多不必要的if-else，也带来了很多微小处的bug。利用栈的思想来处理表达式，也比较面向过程，很多很多的if-else让parse类非常丑陋...但是总体已经有根据指导书及自己的设计往面向对象的方向发展。

Bug分析

这次的强测和互测都比较惨，一个同质Bug引发的血案。总结来说起因还是缺少整体的设计规划。在初步处理时，我没有把表示乘方的**替换为^，然后在分割表达式得出项时，根据我的处理方法，在读到括号外的+或-时，会判断前面是不是 * （规避乘以有符号数以及乘方是有符号数导致错误识别的情况），如果是*，则意味着这是一个有符号数的符号。

if (i != 0 && in.charAt(i - 1) != '*') //这样可以直接规避乘方和乘法两种情况

但是在我为了偷懒替换了乘方符号后，发现此处需要修改，于是直接改为了

if (i != 0 && in.charAt(i - 1) != '^') //遗忘了乘法后的有符号数

所以在出现比如x * +7这种情况时，会将其分为x和+7两项，导致了bug的出现。

Hack环节，使用符合互测长度要求的最长的括号套娃让两个同学出现了TLE。

优缺点分析

优点：分工比较明确，且类之间出现了简单的层次。

缺点：基本放弃了优化，一些设计停留在“能做出来就行”的层次，没有进一步思考有没有更加优雅的处理，导致部分功能的实现（分割项、因子工厂匹配因子等）比较丑陋，增加了思考难度的同时也更容易引发错误。比如在工厂中，因为对正则表达式使用不够熟练，导致无论是三角因子还是幂函数因子，都会匹配出里面的常数变成常数因子，当时的解决方法现在看来也异常丑陋，竟然是调整了匹配顺序，最后匹配常数因子，这也太丑陋了。

第三次作业

本次作业让三角函数可以嵌套任意因子，并且引入了格式判断。基本引用了第二次作业的架构，重写了SinFact和CosFact的deri方法，很快完成了求导部分的拓展。主要工作量落在了WrongFormat的判断。本来想试着写一写递归下降，但是发现那样写基本上就与我本来的架构无关了，递归下降也没学明白。最后，我的思路是在层层解析的过程中逐步分析各层出现的WF。

• 新增了FormatExamine类，检查表达式层面的基本错误。比如括号不匹配、出现不合法字符（arctanx，hello等）、不合理的空格位置（* *，s i n， x ** + 100）等。

• 工厂中匹配到幂函数因子时，检查指数绝对值是否符合规范。

• sin和cos因子求导时，判断括号中是否为多项式，如果是单项式，是否为多个因子，或者是否为空串。

• 本次作业基本与第二次作业无架构变动，所以UML图除了一个单独的FormatExamine类，并无其他差异。

度量分析

 

 

 

 

 

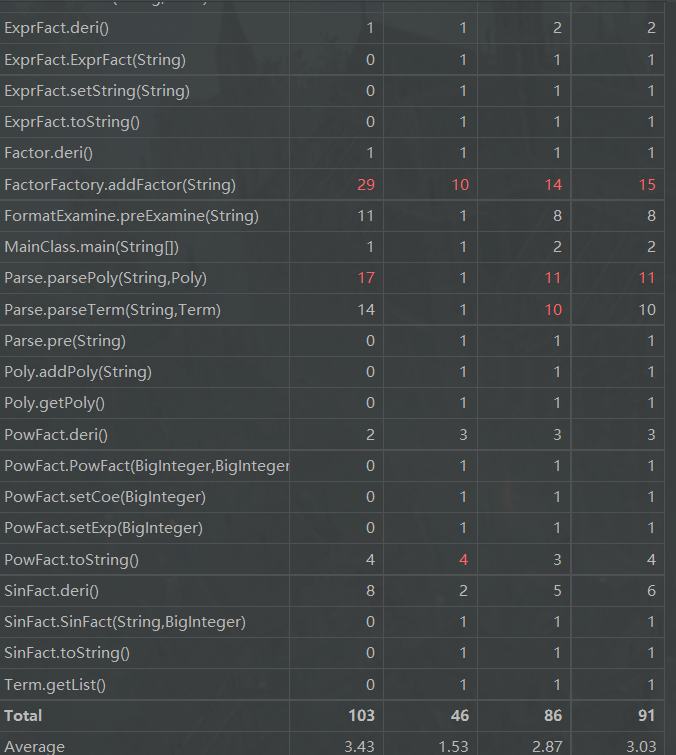
本次作业复杂之处基本与第二次作业相仿，除此之外格式检查类由于特判较多，所以复杂度较高。除此之外，pow类因子用if-else做了较多浅优化，导致了复杂度飙红。

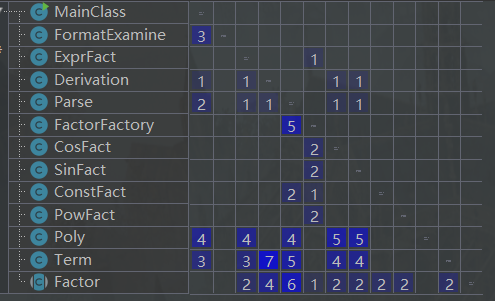
根据关联矩阵，可见各类间的关联度不算太高。

Bug分析

• 在强测的错误格式检查中出现了问题，有几个没想到的遗漏，比如连续乘方。也有已经考虑到但是自己设计没有能够按照预想完成的错误格式检查，比如sin套多层括号，最内侧为空串，根据我的设计，会在读到那对括号后，就确认了因子数为1，而不是0，并且在下一步截去头尾括号时出现了数组越界的异常。

• 在互测中被揪出了一个bug，是我自己确实没考虑到的。这个问题的源头在第二次作业和第三次作业的衔接上。依照我第二次作业的设计，某项在被解析时，如果以负号开头，则会在该项中添加一个常数因子-1，这样与这次格式判断中三角函数里只嵌套因子起了冲突，以sin(-100)为例，我的程序就会将括号内判为-1*100两个因子，导致正确输入错判为错误格式。

• Hack环节，一个同学在使用正则表达式时出现了栈溢出的错误。

优缺点分析

这次作业总体完成度我不太满意，主要谈缺点。首先是没有使用较优的方法完成拓展任务。优化方面，对比第二周只进行了一些浅层次的优化，没有深入。测试方面，覆盖性较差，互测处的bug应该是能通过测试找出来的。

心得体会

1. pre设计得真的很不错，认真做还是收获很多的。pre中涉及的容器、工厂模式、正则表达式对本单元的作业帮助很大。

2. 设计阶段和实现阶段千万不能偷懒、图方便。前面欠的，debug时候总是要还的，逃过debug，公测互测也逃不掉！无论那个阶段，都要尽全力去完成，不仅如此，还得对需求的增加有规划。

3. 无论是课程网站的讨论区，还是与身边同学的讨论，对整体的架构还有细节的处理都有很大的帮助。独学而无友，则孤陋而寡闻。我第一次作业的debug和第二次作业的思路很多都是在和别人的讨论中有了很大进展。

4. 感觉目前为止OO的每个阶段都挺有趣味的，有挑战，也确实有收获。

5. 下次我一定好好研究怎么测试 ！