重链剖分学习笔记
介绍
重链剖分(Tree Line Pow Divide)(Heavy Path Decomposition)是一种将树划分的方法,由 Robert E. Tarjan 于 1983 年发明,可以将根结点到其他某一结点的路径划分为 \(O(\log n)\) 条链,并且可以用其他数据结构高效维护信息。
定义
重(轻)儿子
对某个结点 \(v\) 的儿子结点 \(v_i\),其子树内点的个数最多的某个儿子结点 \(v_i\),被称为结点 \(v\) 的重儿子,其余儿子结点被称为结点 \(v\) 的轻儿子。
重(轻)边
父结点 \(v\) 和其重儿子的连边被称为重边,和轻儿子的连边被称为轻边。
重链
重边互相连接起来形成一条链,这条链就被称为重链。
一个结点也可以被认为在一条重链上,这条重链只包含该点,如作为轻儿子的叶子结点。
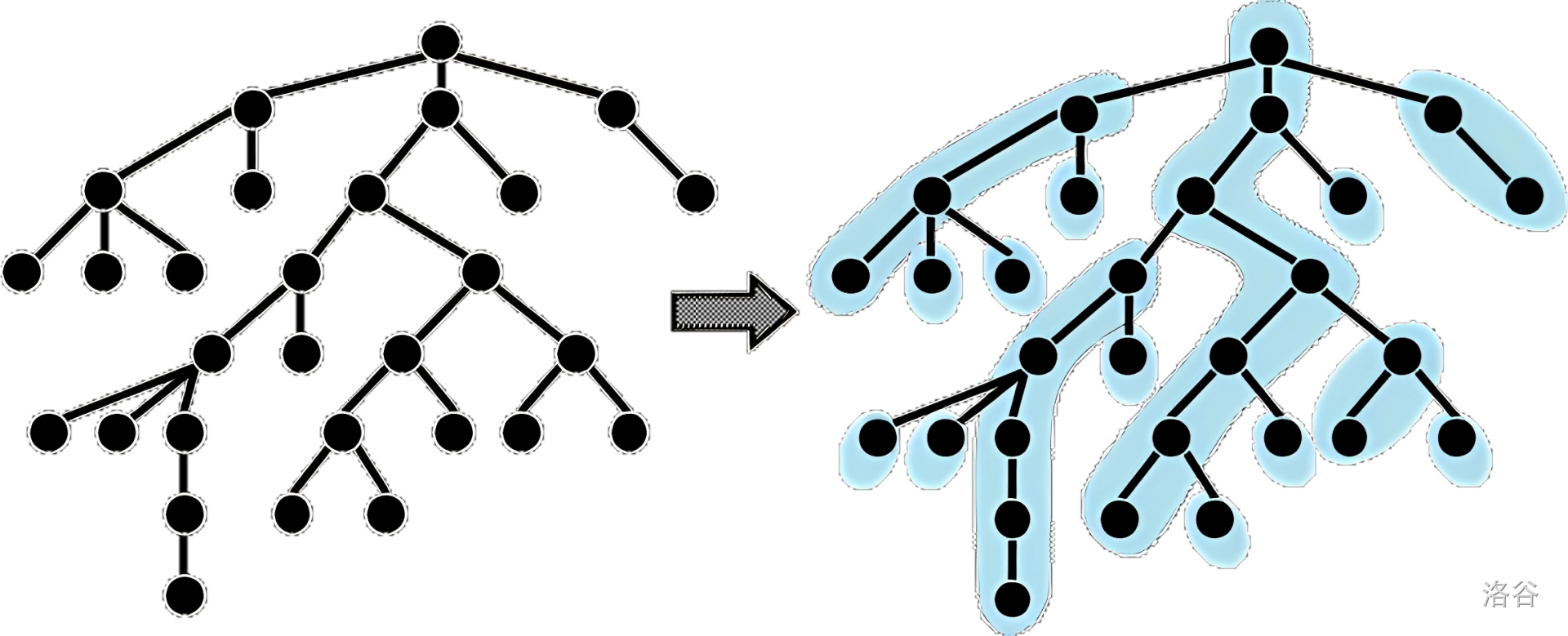
预处理流程
假设有树 \(T = (V, E)\) ,我们对其进行重链剖分。
第一次 DFS
处理出每个点的深度 dep,父亲 fa,子树大小 siz,重儿子 son。
void dfs_1(int x, int f) {
dep[x] = dep[f] + 1, fa[x] = f, siz[x] = 1;
for(int i = head[x]; i; i = ed[i].nxt) {
if(ed[i].to == f) continue;
dfs_1(ed[i].to, x);
siz[x] += siz[ed[i].to];
if(siz[ed[i].to] > siz[son[x]]) son[x] = ed[i].to;
}
}
第二次 DFS
处理出每个点的DFS 序 id,按 DFS 序先后排列的点权 a,这个点所在的重链的顶点 ,即重链上深度 dep 最小的点 top。
DFS 时,优先遍历结点的重儿子。
void dfs_2(int x, int t) {
id[x] = ++tot, a[tot] = v[x], top[x] = t;
if(!son[x]) return;
dfs_2(son[x], t);
for(int i = head[x]; i; i = ed[i].nxt) {
if(ed[i].to == son[x] || ed[i].to == fa[x]) continue;
dfs_2(ed[i].to, ed[i].to);
}
}
复杂度
时间复杂度
这两次 DFS 都要遍历 \(T\) 的 \(n\) 个结点,时间复杂度是 \(O(n)\) 的。
空间复杂度
这两次 DFS 都要处理 \(T\) 的 \(n\) 个结点的相关信息,空间复杂度是 \(O(n)\) 的。
性质
预处理之后,我们有了以下的性质:
性质一
内容
对于某个结点 \(v\),其子树的编号是连续的,且其子树集合恰对应 DFS 序区间 \([id_v, id_v + siz_v - 1]\)。
区间的右端点是 \(id_v + siz_v - 1\) 而非 \(id_v + siz_v\),是因为结点 \(v\) 的子树包含了结点 \(v\) 本身(否则对于一个叶子结点,这是不满足定义的)。
证明
考虑 DFS 序本身的性质,即一次遍历是先遍历某个结点,再遍历它的儿子节点。
性质二
内容
对于一条重链,它的编号是连续的。重链上的一个点 \(v\) 到该重链的顶点 \(top_v\) 经过的所有点,恰对应 DFS 区间 \([id_{top_v}, id_v]\)。
证明
考虑第二次 DFS 的过程。访问一个结点时,优先遍历其重儿子,所以由若干结点 \(v_i\) 组成的重链,这些节点的编号 \(id_{v_i}\) 一定连续。
性质三
内容
轻儿子的子树大小,总不大于其父节点的子树大小的一半。
即对于一条轻边 \(E_i = (u, v)\),\(u\) 是 \(v\) 的父结点,总有 \(siz_v \le \frac{1}{2}siz_u\)。
证明
考虑父结点 \(u\) 的重儿子 \(son_u\)。
反证法。若 \(siz_v > \frac{1}{2}siz_u\),那么 \(siz_{son_u} \le \frac{1}{2}siz_u\)。
即推出 \(siz_{son_u} < siz_v\),说明重儿子的子树大小,比轻儿子的子树大小还小,不符合定义,矛盾!
于是性质三得证。
性质四
内容
一个结点到根结点的简单路径上,最多有 \(O(\log n)\) 条重链,最多有 \(O(\log n)\) 条轻边。
证明
考虑性质三 \(siz_v \le \frac{1}{2}siz_u\)。从根结点向下走,每走过一条轻边,其子树大小至少会变为原来的一半。
根结点的子树大小是 \(n\),一个叶子结点的子树大小为 \(1\),故最多要走 \(O(\log n)\) 条轻边。
对于重链,考虑对于一个作为轻儿子的结点,只要它有儿子,那就必定有一个重儿子,也就是会有重链在它的儿子处产生。
所以,两条重链之间会夹着若干条轻边,考虑一个简单的植树问题,那么重链也有 \(O(\log n)\) 条。
重链之间可以夹着多条轻边,原因是轻儿子也可以有轻儿子。
应用
维护了以上信息,我们可以使用一些数据结构来简便、快速地维护点权或边权。
先给出一棵线段树(维护区间加、区间和)。
struct node {
long long val, tag, l, r;
} t[MAXN * 4];
inline void push_up(int x) {
t[x].val = t[x * 2].val + t[x * 2 + 1].val;
}
inline void push_down(int x) {
(t[x * 2].tag += t[x].tag) %= p, (t[x * 2].val += (t[x * 2].r - t[x * 2].l + 1) * t[x].tag) %= p;
(t[x * 2 + 1].tag += t[x].tag) %= p, (t[x * 2 + 1].val += (t[x * 2 + 1].r - t[x * 2 + 1].l + 1) * t[x].tag) %= p;
t[x].tag = 0;
}
void build(int x, int l, int r) {
t[x].l = l, t[x].r = r;
if(l == r) {
t[x].val = a[l];
return;
}
build(x * 2, l, (l + r) / 2);
build(x * 2 + 1, (l + r) / 2 + 1, r);
push_up(x);
}
void modify(int x, int l, int r, int k) {
int mid = (t[x].l + t[x].r) / 2;
if(l <= t[x].l && t[x].r <= r) {
(t[x].val += (t[x].r - t[x].l + 1) * k) %= p, (t[x].tag += k) %= p;
return;
}
push_down(x);
if(l <= mid) modify(x * 2, l, r, k);
if(mid < r) modify(x * 2 + 1, l, r, k);
push_up(x);
}
long long query(int x, int l, int r) {
int ans = 0, mid = (t[x].l + t[x].r) / 2;
if(l <= t[x].l && t[x].r <= r) return t[x].val;
push_down(x);
if(l <= mid) (ans += query(x * 2, l, r)) %= p;
if(mid < r) (ans += query(x * 2 + 1, l, r)) %= p;
return ans;
}
下面是一些使用重链剖分,用线段树维护具体信息的例子。
维护树上某结点的子树中结点点的权值
考虑性质一,在 DFS 序区间 \([id_v, id_v + siz_v - 1]\) 上用线段树维护即可。
时间复杂度为 \(O(\log n)\)。
inline void modify_subtree(int x, int k) {
modify(1, id[x], id[x] + siz[x] - 1, k);
}
inline long long query_subtree(int x) {
return query(1, id[x], id[x] + siz[x] - 1);
}
维护树上两结点简单路径上的点权和
考虑性质二。设这两个点为 \(u, v\)。
分情况讨论。
- 如果 \(u\) 和 \(v\) 在同一条重链上,即 \(top_u = top_v\) 时,设 \(dep_u < dep_v\), 两点路径上的点就是 DFS 区间 \([id_u, id_v]\);
- 如果 \(u\) 和 \(v\) 不在同一条重链上,即 \(top_u \neq top_v\) 时,我们不断让重链顶端较深的一个点向上跳,跳到这条重链顶点的父结点,即假设 \(dep_{top_u} > dep_{top_v}\),让 \(u \gets fa_{top_u}\),直到 \(top_u = top_v\),每次跳的时候维护 DFS 区间 \([id_{top_u}, id_u]\);
以求点权和为例,写出伪代码如下:
query_range u, v
ans = 0
while top_u is not top_v
if dep_top_u < dep_top_v
swap u, v
ans = ans + dfs_order val range [id_top_u, id_u]
u = fa_top_u
if dep_u > dep_v
swap u, v
ans = ans + dfs_order val_range [id_u, id_v]
return ans
性质四告诉我们,某个点到根结点的路径上有 \(O(\log n)\) 条重链。把 \(u\) 和 \(v\) 的最近公共祖先看作根结点,\(u\) 和 \(v\) 分别到根结点的路径上有 \(O(\log n)\) 条重链,每次跳过一条重链需要用 \(O(\log n)\) 时间(这个时间由选择的数据结构决定)更新答案,所以时间复杂度为 \(O(\log n \times \log n) = O(\log ^ 2 n)\)。
inline void modify_path(int u, int v, int k) {
while(top[u] != top[v]) {
if(dep[top[u]] < dep[top[v]]) u ^= v ^= u ^= v;
modify(1, id[top[u]], id[u], k);
u = fa[top[u]];
}
if(dep[u] > dep[v]) u ^= v ^= u ^= v;
modify(1, id[u], id[v], k);
}
inline long long query_path(int u, int v) {
long long ans = 0;
while(top[u] != top[v]) {
if(dep[top[u]] < dep[top[v]]) u ^= v ^= u ^= v;
(ans += query(1, id[top[u]], id[u])) %= p;
u = fa[top[u]];
}
if(dep[u] > dep[v]) u ^= v ^= u ^= v;
(ans += query(1, id[u], id[v])) %= p;
return ans;
}
类似地,也能用这样的思想在 \(O(\log n)\) 的时间内求两点的最近公共祖先,并且常数较小。
维护树上两结点简单路径上的边权和
将一条边的权值拍到两点中深度较大的点权上,其余部分同点权和。
但是两点在同一条链上时,维护的 DFS 区间应该是 \([id_u, id_v - 1]\) 而不是 \([id_u, id_v]\),原因是这时的结点 \(v\) (原来的结点 \(u\) 和结点 \(v\) 的最近公共祖先)的点权是 \(u\) 和 \(v\) 的最近公共祖先和其父结点的边权,不应该包括在答案中。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号