取样和取样函数的傅里叶变换
取样
在用计算机处理之前,需要将连续函数处理成为离散值序列,考虑一个连续函数\(f(t)\),模拟取样的一种方法是用一个\(\Delta T\)单位间隔的冲激串作为取样函数去乘以\(f(t)\):
\[\tilde{f}(t) = f(t)s_{\Delta T}(t) = \sum_{n = -\infty}^{\infty}f(t)\delta(t - n\Delta T)
\]
其中\(\tilde{f}(t)\)表示取样后的函数,每个取样值由加权后的冲激强度给出,可以通过积分得到,也就是序列中任意取样值\(f_k\)由下式给出:
\[f_k = \int_{-\infty}^{\infty}f(t)\delta(t - k\Delta T)dt = f(k\Delta T),k = \cdots,-2,-1,0,1,2,\cdots
\]
![对连续函数取样]()
取样函数的傅里叶函数
令\(F(\mu)\)表示\(f(t)\)的傅里叶变换,取样之后的相应函数\(\tilde{f}(t)\)是\(f(t)\)与一个冲激串的乘积,而空间域中两个函数乘积的傅里叶变换是两个函数傅里叶变换的卷积:
\[\tilde{F}(\mu) = \mathfrak{J}\{\tilde{f}(t)\} = \mathfrak{J}\left\{f(t)s_{\Delta T}(t)\right\} = F(\mu) ★S(\mu)
\]
冲激串的傅里叶变换:
\[S(\mu) = \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}\delta(t - \frac{n}{\Delta T})
\]
可以得到:
\[\begin{aligned}
\tilde{F}(\mu)
&= F(\mu) ★S(\mu) \\
&= \int_{-\infty}^{\infty}F(\tau)S(\mu - \tau)d\tau \\
&= \frac{1}{\Delta T}\int_{-\infty}^{\infty}F(\tau)\sum_{n = -\infty}^{\infty}\delta\left(\mu - \tau - \frac{n}{\Delta T}\right)d\tau \\
&= \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}\int_{-\infty}^{\infty}F(\tau)\delta\left(\mu - \tau - \frac{n}{\Delta T}\right)d\tau \\
&= \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}F\left(\mu - \frac{n}{\Delta T}\right)
\end{aligned}
\]
得到取样后的函数\(\tilde{f}(t)\)的傅里叶变换\(\tilde{F}(\mu)\)是\(F(\mu)\)的一个拷贝的无限、周期序列,拷贝的间隔为\(\frac{1}{\Delta T}\),可以看到取样之后的函数是离散的,但是取样之后的函数的傅里叶变换是连续的
下图是原函数的傅里叶变换简图:
![原函数的傅里叶变换简图]()
过采样:
![过采样的结果]()
临界采样:
![临界采样的结果]()
取样定理
对于以原点为中心的有限区间\([-\mu_{max},\mu_{max}]\)之外的频率值,其傅里叶变换为0的函数\(f(t)\)称为带限函数,如上第一幅图,如果可以从\(\tilde{F}(\mu)\)中分离出\(F(\mu)\)的一个拷贝,那么我们就可以从取样后的版本利用反变换复原出\(f(t)\),条件如下:
\[\frac{1}{2}\Delta T \gt \mu_{max}
\]
也就是以超过最高频率的两倍的取样率来获得样本,连续的带限函数就可以完全从它的样本集来恢复,也就是不会产生信息损失,完全等于最高频率的两倍的取样率称为奈奎斯特取样率
- 恢复原函数的过程:
一个低通滤波器\(H(\mu)\):
\[H(\mu) =
\begin{cases}
\Delta T & -\mu_{max} \leq \mu \leq \mu_{max} \\
0 & otherwise
\end{cases}
\]
这个和取样之后的函数的傅里叶变换\(\tilde{F}(\mu)\)相乘,取样率需要大于奈奎斯特取样率:
\[F(\mu) = H(\mu)\tilde{F}(\mu)
\]
得到\(F(\mu)\)之后就可以通过傅里叶反变换复原\(f(t)\):
\[f(t) = \int_{-\infty}^{\infty}F(\mu)e^{j2\pi\mu t}d\mu
\]
混淆
一个带限函数用低于其最高频率的两倍取样率取样将会出现周期重叠,此时不管使用什么滤波器,都不可能分理出变换的一个周期,这种效果就是频率混淆,简称为混淆;
除了一些特殊情况以外,在取样过的函数中,混淆总是存在的,在我们限制函数的持续时间时,总会引入无限的频率分量,例如,假设我们想要把带限函数\(f(t)\)的持续时间限制在区间\([0,T]\)内,可以让\(f(t)\)乘如下函数达到:
\[h(t) = \begin{cases}
1 & 0 \leq t \leq T \\
0 & otherwise
\end{cases}
\]
我们知道两个函数乘积的傅里叶变换等于两个函数的傅里叶变换的卷积,\(f(t)\)的变换是带限的,但是\(h(t)\)的傅里叶变换在频率域上是无限延伸的,所以卷积之后得到一个频率分量无限扩展的结果
由取样后的数据重建(复原)函数
\[f(t) = \mathfrak{J}^{-1}\{F(\mu)\} = \mathfrak{J}^{-1}\{H(\mu)\tilde{F}(\mu)\} = h(t)★\tilde{f}(t)
\]
又有:
\[\tilde{f}(t) = f(t)s_{\Delta T}(t) = \sum_{n = -\infty}^{\infty}f(t)\delta(t - n\Delta T)
\]
盒装滤波器\(H(\mu)\)的傅里叶反变换是一个\(sinc\)函数:
\[f(t) = \sum_{n = -\infty}^{\infty}f(n\Delta T)sinc[(t - n\Delta T)/\Delta T]
\]
对于\(t = k\Delta T\),\(f(t)\)等于第\(k\)个样本\(f(k\Delta T)\),样本点之间的\(f(t)\)是由\(sinc\)函数的和形成的内插
单变量的离散傅里叶变换DFT
由取样后的函数的连续变换得到DFT
由上面的基础知识可以得到取样后的离散函数的傅里叶变换:
\[\begin{aligned}
\tilde{F}(\mu)
&= \int_{-\infty}^\infty\tilde{f}(t)e^{-j2\pi\mu t}dt \\
&= \int_{-\infty}^{\infty}\sum_{n = -\infty}^{\infty}f(t)\delta(t - n\Delta T)e^{-j2\pi\mu t}dt \\
&= \sum_{n = -\infty}^{\infty}\int_{-\infty}^\infty f(t)\delta(t - n\Delta T)e^{-j2\pi\mu t}dt \\
&= \sum_{n = -\infty}^{\infty}f_ne^{-j2\pi\mu n\Delta T}
\end{aligned}
\]
从之前的推导中有:
\[\begin{aligned}
\tilde{F}(\mu)
&= F(\mu) ★S(\mu) \\
&= \int_{-\infty}^{\infty}F(\tau)S(\mu - \tau)d\tau \\
&= \frac{1}{\Delta T}\int_{-\infty}^{\infty}F(\tau)\sum_{n = -\infty}^{\infty}\delta\left(\mu - \tau - \frac{n}{\Delta T}\right)d\tau \\
&= \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}\int_{-\infty}^{\infty}F(\tau)\delta\left(\mu - \tau - \frac{n}{\Delta T}\right)d\tau \\
&= \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}F\left(\mu - \frac{n}{\Delta T}\right)
\end{aligned}
\]
也就是\(\tilde{F}(\mu)\)是一个周期为\(\frac{1}{\Delta T}\)的函数,我们需要表征\(\tilde{F}(\mu)\)的一个周期,假设在周期\(\mu = 0\)到\(\mu = \frac{1}{\Delta T}\)之间等间距的得到\(\tilde{F}(\mu)\)的\(M\)个样本,也就是在如下频率处取样:
\[\mu = \frac{m}{M \Delta T},m = 0, 1,2,\cdots,M-1
\]
将\(\mu\)带到上面的式子:
\[F_m = \sum_{n = 0}^{M - 1}f_ne^{-j2\pi mn/M},m = 0,1,2,\cdots,M - 1
\]
上式就是离散傅里叶变换,给定一个由\(f(t)\)的\(M\)个样本组成的集合\(\{f_n\}\),上式可以得到一个与输入样本集合离散傅里叶变换相对应的\(M\)个复数离散值的样本集合\(\{F_m\}\),相反的,我们可以用傅里叶反变换\(IDFT\)复原样本集:
\[f_n = \frac{1}{M}\sum_{m = 0}^{M - 1}F_me^{j2\pi mn / M},n - 0,1,2,\cdots,M - 1
\]
上面的两个式子构成离散傅里叶变换对,离散傅里叶变换对适用于任何均匀取样的有限离散样本集,一般使用\(x,y\)表示坐标变量,\(u,v\)表示频率变量,离散傅里叶变换对变为:
\[F(u) = \sum_{x = 0}^{M - 1}f(x)e^{-j2\pi u x / M} \\
f(x) = \frac{1}{M}\sum_{u = 0}^{M - 1}F(u)e^{j2\pi u x / M}
\]
可以证明傅里叶正变换和反变换都是无限周期的,其周期为\(M\):
\[F(u) = F(u + kM) \\
f(x) = f(x + kM)
\]
卷积的离散表示为:
\[f(x) ★ h(x) = \sum_{m = 0}^{M - 1}f(m)h(x - m),x = 0,1,2,\cdots,M-1
\]
取样和频率间隔间的关系
如果\(f(x)\)由函数\(f(t)\)以\(\Delta T\)为单位间隔取样后的\(M\)个样本组成,则包含集合\(\{f(x)\},x = 0,1,2,\cdots,M - 1\)的记录的持续时间为:
\[T = M\Delta T
\]
离散频率域中的相应间隔为:
\[\Delta u = \frac{1}{M\Delta T} = \frac{1}{T}
\]
\(M\)个分量跨越的频率范围为:
\[\Omega = M\Delta u = \frac{1}{\Delta T}
\]
两个变量的函数的扩展
二维冲激及其取样特性
两个连续变量\(t,z\)的冲激\(\delta(t,z)\)被定义为:
\[\delta(t,z) = \begin{cases}
\infty & t = z = 0 \\
0 & otherwise
\end{cases}
\]
且:
\[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\delta(t,z)dtdz = 1
\]
在积分情况下显示取样特性:
\[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)\delta(t,z)dtdz = f(0,0)
\]
更一般的在\(t_0,z_0\)处:
\[\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)\delta(t - t_0,z - z_0)dtdz = f(t_0,z_0)
\]
对于离散变量\(x,y\),二维离散冲激定义为:
\[\delta(x,y) = \begin{cases}
1 & x = y = 0 \\
0 & otherwise
\end{cases}
\]
其取样特性为:
\[\sum_{x = -\infty}^{\infty}\sum_{y = -\infty}^{\infty}f(x,y)\delta(x, y) = f(0,0)
\]
对于一个在\((x_0,y_0)\)处的冲击:
\[\sum_{x = -\infty}^{\infty}\sum_{y = -\infty}^{\infty}f(x,y)\delta(x - x_0,y - y_0) = f(x_0,y_0)
\]
离散冲激的取样特性就是在冲激所在位置产生离散函数\(f(x,y)\)的值
二维连续傅里叶变换对
\[F(\mu,v) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)e^{-j2\pi(\mu t + vz)}dtdz \\
f(t,z) = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}F(\mu,v)e^{j2\pi(\mu t + v z)}d\mu dv
\]
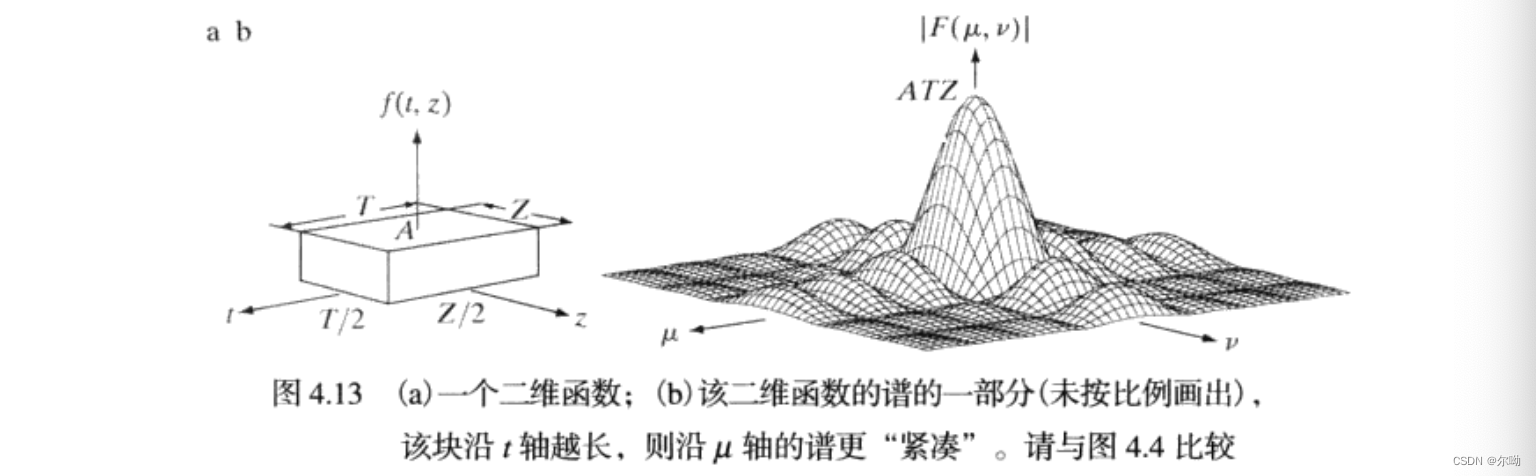
- 和一维连续离散对类似的例子:
![盒装函数]()
\[\begin{aligned}
F(\mu,v)
&= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(t,z)e^{-j2\pi(\mu t + vz)}dtdz \\
&= \int_{-\frac{T}{2}}^{\frac{T}{2}} \int_{-\frac{Z}{2}}^{\frac{Z}{2}} A e^{-j2\pi(\mu t + vz)}dtdz \\
&= ATZ\left[\frac{\sin (\pi\mu T)}{\pi\mu T} \right]\left[\frac{\sin (\pi v Z)}{\pi v Z}\right]
\end{aligned}
\]
和一维类似的,傅里叶变换中值为0的位置和\(T,Z\)成反比
二维取样和二维取样定理
二维冲激串:
\[s_{\Delta T\Delta Z}(t,z) = \sum_{m = -\infty}^{\infty}\sum_{n = -\infty}^{\infty}\delta(t - m\Delta T,z - n\Delta Z)
\]
用上述冲激串和二维连续函数相乘可以得到取样之后的函数,如果由区间\([-\mu_{max},\mu_{max}]\)和区间\([-v_{max},v_{max}]\)建立的矩形之外的傅里叶变换为0,那么\(f(t,z)\)称为带限函数:
\[F(\mu,v) = 0,|\mu|\geq \mu_{max},|v| \geq v_{max}
\]
二维取样定理表面,如果取样间隔满足:
\[\Delta T \lt \frac{1}{2\mu_{max}},\Delta Z \lt \frac{1}{2v_{max}}
\]
或者取样率满足:
\[\frac{1}{\Delta T} \gt 2\mu_{max}, \frac{1}{\Delta Z} \gt 2v_{max}
\]
那么连续带限函数\(f(t,z)\)可以从一组样本无误的恢复
图像中的混淆
- 主要存在两种混淆现象:空间混淆和时间混淆,空间混淆是由于欠取样造成的;
- 抗混淆滤波是需要在图像被取样之前要做的,不存在事后用抗混淆滤波器来减少由于违反取样定理导致的混淆的影响;
- 缩小图像可以看成欠采样,通过行列删除实现,为减小混淆,在缩小图像之前可以先稍微模糊一下图像,例如使用均值滤波器来平滑图像;
- 莫尔(波纹)效应:在数字图像处理中,当扫描介质印刷物如报纸和杂志时,或者在具有周期分量的图像中,如果他的间隔与取样的间隔可比的时候,会出现,例如将两面纱窗叠放在一起产生的现象,也就是会产生一幅在原始模式中均不出现的差拍模式;
二维离散傅里叶变换及其反变换
下式是二维傅里叶变换\(DFT\)
\[F(\mu,v) = \sum_{x = 0}^{M - 1}\sum_{y = 0}^{N - 1}f(x,y)e^{-j2\pi(\mu x / M + vy / N)}
\]
其中\(f(x,y)\)是大小为\(M \times N\)的数字图像,当给出\(F(\mu,v)\)的呀得到傅里叶反变换\(IDFT\):
\[f(x,y) = \frac{1}{MN}\sum_{\mu = 0}^{M - 1}\sum_{v = 0}^{N - 1}F(\mu,v)e^{j2\pi(\mu x / M + vy / N)}
\]




![盒装函数]()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号