背景
- 傅里叶指出:任何周期函数都可以表示为不同频率的正弦和/或余弦之和的形式,每个正弦项和/或余弦项乘以不同的系数(现在称该和为傅里叶级数);
- 傅里叶变换:非周期函数(该曲线下的面积是有限的)也可以用正弦和/或余弦乘以加权函数的积分来表示;
- 用傅里叶级数或变换表示的函数特征完全可以通过傅里叶反变换来重建,而不会丢失任何信息;
基本概念
复数
\(R,I\)是实数,\(R\)表示复数的实部,\(I\)是复数的虚部,\(j\)是一个等于\(-1\)的平方根的虚数,\(j = \sqrt{-1}\),复数\(C\)定义如下:
\[C = R + jI
\]
一个复数\(C\)的共轭表示为\(C^*\):
\[C^* = R - jI
\]
复数可以看做是复平面上的一个点,横坐标是实轴值为\(R\),纵坐标是虚轴值\(I\),在极坐标下表示复数:
\[C = |C|(\cos \theta + j\sin \theta)
\]
其中\(|C| = \sqrt{R^2 + I^2},\theta = \arctan(\frac{I}{R}),\theta \in [-\pi,\pi]\),使用欧拉公式:
\[e^{j\theta} = \cos \theta + j\sin \theta
\]
其中\(e = 2.71828\cdots\),可得到复数表示:
\[C = |C|e^{j\theta}
\]
傅里叶级数
具有周期\(T\)的连续变量\(t\)的周期函数\(f(t)\)可以被描述为乘以适当系数的正弦和余弦和,这个和就是傅里叶级数,具有如下形式:
\[f(t) = \sum_{n = -\infty}^{\infty}c_ne^{j\frac{2\pi n}{T}t}
\]
其中:
\[c_n = \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-j\frac{2\pi n}{T}t}dt,n = 0,\pm 1,\pm 2,\cdots
\]
冲激及其取样特性
连续变量\(t\)在\(t = 0\)处的单位冲激表示为\(\delta(t)\),定义为:
\[\delta(t) = \begin{cases}
\infty & t = 0 \\
0 & t \neq 0
\end{cases}
\]
且满足等式:
\[\int_{-\infty}^{\infty}\delta(t)dt = 1
\]
物理上,如果我们把\(t\)解释为时间,那么一个冲激可看成是幅度无限,持续时间为0,具有单位面积的一个尖峰信号,一个冲激具有关于如下积分的所谓取样特性:
\[\int_{-\infty}^{\infty}f(t)\delta(t)dt = f(0)
\]
取样特性的更一般的说明涉及位于任意点\(t_0\)的冲激,表示为\(\delta(t - t_0)\),此时取样特性变为:
\[\int_{-\infty}^{\infty}f(t)\delta(t - t_0)dt = f(t_0)
\]
令\(x\)表示一个离散变量,单位离散冲激\(\delta(x)\)在离散系统中的作用与处理连续变量时冲激\(\delta(t)\)的作用相同,定义如下:
\[\delta(x) = \begin{cases}
1 & x = 0 \\
0 & x \neq 0
\end{cases}
\]
且满足等式:
\[\sum_{x = -\infty}^{\infty}\delta(x) = 1
\]
离散变量的取样特性有如下形式:
\[\sum_{x = -\infty}^{\infty}f(x)\delta(x) = f(0)
\]
更一般的用\(x = x_0\)处的离散冲激:
\[\sum_{x = -\infty}^{\infty}f(x)\delta(x - x_0) = f(x_0)
\]
冲激串\(s_{\Delta T}(t) = \sum_{n = -\infty}^{\infty}\delta(t - n\Delta T)\)
连续变量函数的傅里叶变换
由\(\mathfrak{J}\{f(t)\}\)表示连续变量\(t\)的连续函数\(f(t)\)的傅里叶变换由下式定义:
\[\mathfrak{J}\{f(t)\} = \int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt
\]
其中\(\mu\)也是一个连续变量,因为\(t\)被积分过了,故\(\mathfrak{J}\{f(t)\}\)仅是\(\mu\)的函数,为了明确这一个事实,我们把傅里叶变换写成\(\mathfrak{J}\{f(t)\} = F(\mu)\):
\[F(\mu) = \int_{-\infty}^{\infty}f(t)e^{-j2\pi \mu t}dt
\]
相反,给定\(F(\mu)\),通过傅里叶反变换可以获得\(f(t)\),即\(f(t) = \mathfrak{J}^{-1}\{F(\mu)\}\)
\[f(t) = \int_{-\infty}^{\infty}F(\mu)e^{j2\pi \mu t}d\mu
\]
可以看到\(\mu\)被积分过了,可以简单的写成\(f(t)\),正变换和反变换合起来称作傅里叶变换对,如果使用欧拉公式:
\[F(\mu) = \int_{-\infty}^{\infty}f(t)[\cos(2\pi\mu t) - j\sin(2\pi\mu t)]dt
\]
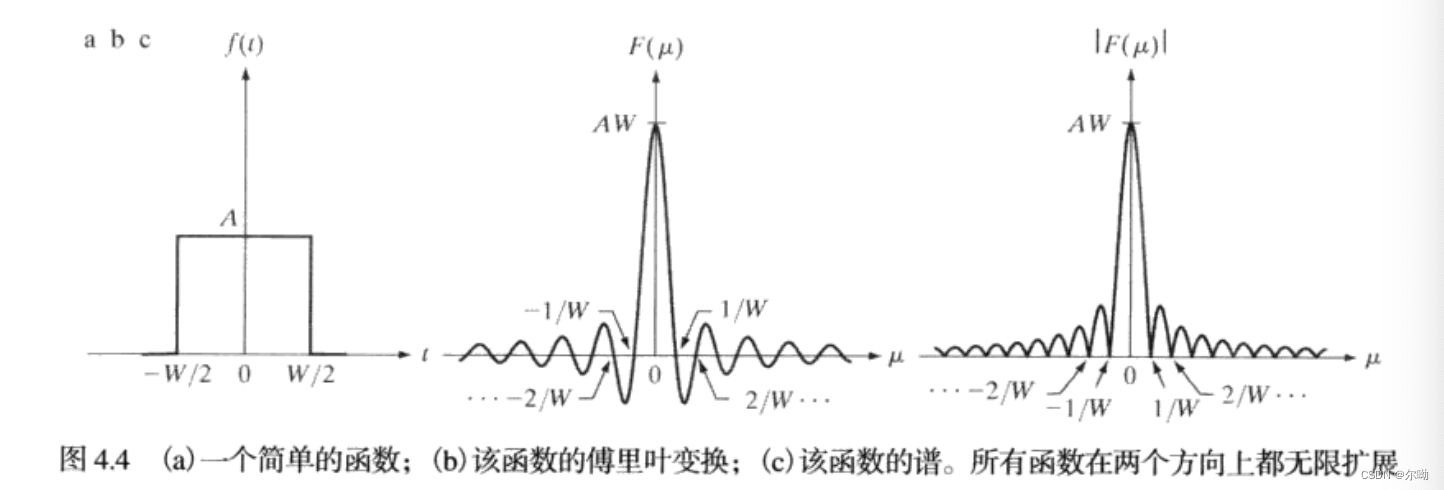
- 例1:三角学恒等式\(\sin \theta = (e^{j\theta} - e^{-j\theta})/2j\),盒状函数的傅里叶变换:\(F(\mu),|F(\mu)|\)的零值位置与盒状函数的宽度\(W\)成反比
\[\begin{aligned}
F(\mu)
&= \int_{-\infty}^{\infty}f(t)e^{-j2\pi\mu t}dt \\
&= \int_{-\frac{W}{2}}^{\frac{W}{2}}Ae^{-j2\pi\mu t}dt \\
&= \frac{-A}{j2\pi\mu}\left[e^{-j2\pi\mu t}\right]_{-\frac{W}{2}}^{\frac{W}{2}} \\
&= \frac{-A}{j2\pi\mu}\left[e^{-j\pi\mu W} - e^{j\pi\mu W}\right] \\
&= \frac{A}{j2\pi\mu}\left[e^{j\pi\mu W} - e^{-j\pi\mu W}\right] \\
&= AW\frac{\sin(\pi\mu W)}{\pi\mu W}
\end{aligned}
\]
对于\(sinc\)函数,有\(sinc(m) = \frac{sin(\pi m)}{\pi m}\),在\(m = 0\)时函数值为1,在\(m\)为其他整数值的时候函数值为0;
![盒状函数的傅里叶变换]()
- 例2:冲激和冲激串的傅里叶变换:一个位于空间域原点的傅里叶变换,在频率域是一个常数
\[F(\mu) = \int_{-\infty}^{\infty}\delta(t)e^{-j2\pi \mu t}dt = \int_{-\infty}^{\infty}e^{-j2\pi \mu t}\delta(t)dt = e^{-j2\pi \mu 0} = e^0 = 1
\]
在\(t = t_0\)的一个冲激的傅里叶变换:
\[F(\mu) = \int_{-\infty}^{\infty}\delta(t - t_0)e^{-j2\pi \mu t}dt = \int_{-\infty}^{\infty}e^{-j2\pi \mu t}\delta(t - t_0)dt = e^{-j2\pi \mu t_0} = \cos(2\pi \mu t_0) - j\sin(2\pi \mu t_0)
\]
冲激串的傅里叶变换:冲激串\(s_{\Delta T}(t)\)是周期为\(\Delta T\)的周期函数,所以可以表示为傅里叶级数:
\[s_{\Delta T}(t) = \sum_{n = -\infty}^{\infty}c_ne^{j\frac{2\pi n}{\Delta T}t}
\]
其中:
\[c_n = \frac{1}{\Delta T}\int_{-\frac{\Delta T}{2}}^{\frac{\Delta T}{2}}s_{\Delta T}(t)e^{-j\frac{2\pi n}{\Delta T}t}dt
\]
可以看到区间\([-\frac{\Delta T}{2},\frac{\Delta T}{2}]\)范围内只包含位于原点的冲激,所以上式变为:
\[c_n = \frac{1}{\Delta T}\int_{-\frac{\Delta T}{2}}^{\frac{\Delta T}{2}}\delta(t)e^{-j\frac{2\pi n}{\Delta T}t}dt = \frac{1}{\Delta T}e^0 = \frac{1}{\Delta T}
\]
然后傅里叶级数展开为:
\[s_{\Delta T}(t) = \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}e^{j\frac{2\pi n}{\Delta T}t}
\]
目的是得到上式的傅里叶变换,因为求和是线性过程,得到和的傅里叶变换与求各个分量的傅里叶变换之和是相同的:
\[\mathfrak{J}\left\{e^{j\frac{2\pi n}{\Delta T}t}\right\} = \delta\left(\mu - \frac{n}{\Delta T}\right)
\]
因此周期冲激串\(s_{\Delta T}(t)\)的傅里叶变换\(S(\mu)\)为:
\[\begin{aligned}
S(\mu)
&= \mathfrak{J}\left\{s_{\Delta T}(t)\right\} \\
&= \mathfrak{J}\left\{\frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}e^{j\frac{2\pi n}{\Delta T}t}\right\} \\
&= \frac{1}{\Delta T}\mathfrak{J}\left\{\sum_{n = -\infty}^{\infty}e^{j\frac{2\pi n}{\Delta T}t}\right\} \\
&= \frac{1}{\Delta T}\sum_{n = -\infty}^{\infty}\delta\left(\mu - \frac{n}{\Delta T}\right)
\end{aligned}
\]
周期为\(\Delta T\)的冲激串的傅里叶变换还是冲激串,其周期为\(\frac{1}{\Delta T}\)
卷积
具有连续变量\(t\)的两个连续函数\(f(t),h(t)\)的卷积:
\[f(t)★h(t) = \int_{-\infty}^{\infty}f(\tau)h(t - \tau)d\tau
\]
上式的傅里叶变换:
\[\begin{aligned}
\mathfrak{J}\left\{f(t)★h(t)\right\}
&= \int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}f(\tau)h(t - \tau)d\tau\right]e^{-j2\pi\mu t}dt \\
&= \int_{-\infty}^{\infty}f(\tau)\left[\int_{-\infty}^{\infty}h(t - \tau)e^{-j2\pi\mu t}dt\right]d\tau \\
&= \int_{-\infty}^{\infty}f(\tau)\left[H(\mu)e^{-j2\pi\mu\tau}\right]d\tau \\
&= H(\mu)\int_{-\infty}^{\infty}f(\tau)e^{-j2\pi\mu\tau}d\tau \\
&= H(\mu)F(\mu)
\end{aligned}
\]
\(H(\mu)\)是\(h(t)\)的傅里叶变换,可以推得空间域中两个函数的卷积的傅里叶变换等于两个函数的傅里叶变换在频率域的乘积,也就是说假如有两个变换的乘积,那么进行傅里叶反变换就可以得到空间域的卷积


 浙公网安备 33010602011771号
浙公网安备 33010602011771号