高级人工智能-lecture2-搜索问题

本文主要讨论基于目标的Agent中的一种，称为问题求解Agent，要进行问题求解，首先要讨论的是对问题及其解的精确定义，将通过一些实例来说明如何描述一个问题及其解，接着介绍一些求解此类问题的通用的搜索算法，包括无信息搜索算法和有信息的搜索算法。

搜索问题

目标是世界的一个状态集合，是目标被满足的那些状态的集合，任务是找到现在和未来如何行动，以使达到一个目标状态。

搜索问题构成：

• 输入：问题
• 输出：问题的解

构成（五个部分）问题的输入

• Agent的初始状态
• 描述Agent的可能行动：在给定的状态$s$下，Agent可以采取的动作$ACTIONS(s)$
• 转移模型：对每个模型的描述，在状态$s$下采取动作$a$后达到的状态$RESULT(s,a)$，也称为后继状态
• 状态空间：初始状态、行动和转移模型无疑就定义了问题的状态空间，即从初始状态可以达到的所有的状态的集合。状态空间形成一个有向网络或图，其中结点表示状态，结点之间的弧表示行动
• 目标测试：确定给定的状态是不是目标状态
• 路径耗散函数为每条路径赋一个耗散值，即边加权。

输出：解是一个行动序列，将初始状态转换成目标状态，解的质量由路径耗散函数度量，所有解里路径耗散值最小的解即为最优解。

搜索树

• 根节点对应了初始状态
• 子节点对应了父节点的后继
• 节点显示状态，但对应的是到达这些状态的行动

一般的树搜索

搜索算法特性：

• 完备性，当问题有解时，保证能找到一个解
• 最优性：保证能找到最优解
• 时间复杂度
• 空间复杂度

以下面三个值来计算

• $b$：分支因子，任何节点的最多后继数
• $d$：目标节点所在的最浅的深度，如从根节点到目标状态的步数
• $m$：状态空间中任何路径的最大长度

节点的类别：

• 扩展的节点：扩展之后就是访问过的节点
• 生成的节点：入队列的节点，等待被扩展

图搜索

主要思想：不要扩展一个状态两次
执行：

• 树搜索+扩展过的状态集closed set
• 将节点扩展成搜索树
• 扩展节点之前，检查确保它的状态在之前没有被扩展
• 如果不是新的状态，忽略；如果是新的，加入到closed set

无信息的搜索算法uninformed

无信息搜索指的是除了问题定义中提供的状态信息外没有任何附加信息。

广度优先搜索

• 完备性：可以保证
• 最优性：只有当每个路线的代价都是一样的时候
• 时间复杂度：$b+b^2 + b^3 + \cdots + b^d = O(b^d)$
• 空间复杂度：对任何类型的图搜索，每个已扩展的结点都保存在探索集中，空间复杂度总是在时间复杂度的 $b$ 分之一内。特别对于宽度优先图搜索，每个生成的结点都在内存中。那么将有$O(b^{d - 1})$个结点在探索集中，$O(b^d)$个结点在边缘结点集中。所以空间复杂度为 $O(b^d)$
• 可以在节点扩展时或者生成时进行目标测试

代价一致搜索uniform cost search

深度优先搜索知识找到了行动次数最少得路线，但是没有考虑到代价这一个因素-也就是最小生成树

• 完备性：可以满足
• 最优性：可以满足
• 一致代价搜索由路径代价而不是深度来引导，所以算法复杂度不能简单地用$b$和$d$来表示。引入$C^*$表示最优解的代价，假设每个行动的代价至少为$\varepsilon$，那么最坏情况下，算法的时间和空间复杂度为$O(b^{1+\lfloor C^* / \varepsilon \rfloor})$要比$O(b^d)$大得多。这是因为一致代价搜索在探索包含代价大的行动之前，经常会先探索代价小的行动步骤所在的很大的搜索树。当所有的单步耗散都相等的时候，$O(b^{1+\lfloor C^* / \varepsilon \rfloor})$就是$O(b^d)$。此时，一致代价搜索与宽度优先搜索类似，除了算法终止条件，宽度优先搜索在找到解时终止，而一致代价搜索则会检査目标深度的所有结点看谁的代价最小;这样，在这种情况下一致代价搜索在深度无意义地做了更多的工作。
• 在节点被扩展时进行目标测试

深度优先搜索

• 完备性：深度可能是无限的，需要避免环的出现
• 最优性：没有，总是寻找最左边的路线，没有考虑深度和代价
• 时间复杂度：深度优先搜索的时间复杂度受限于状态空间的规模(当然，也可能是无限的 )另一方面，深度优先的树搜索，可能在搜索树上生成所有 $O(b^m)$个结点，其中 $m$ 指的是任一结点的最大深度;这可能比状态空间大很多。要注意的是 $m$ 可能比 $d$ (最浅解的深度)大很多， 并且如果树是无界限的，$m$ 可能是无限的。
• 空间复杂度：深度优先搜索只需要存储一条从根结点到叶结点的路径，以及该路径上每个结点的所有未被扩展的兄弟结点即可。一旦一 个结点被扩展，当它的所有后代都被探索过后该结点就从内存中删除。考虑状态空间分支因子为$b$最大深度为$m$ 深度优先搜索只需要存储$O(bm)$个结点.

深度受限搜索

在无限状态空间深度优先搜索会令人尴尬地失败，而这个问题可以通过对深度优先搜索设置界限 $l$来避免。就是说，深度为$l$的结点被当作没有后继对待。这种方法称为深度受限搜索 (depth-limited search)。

• 完备性：如果我们选 择了$l \lt d$，即是说，最浅的目标结点的深度超过了深度限制，那么这种搜索算法是不完备的。
• 最优性：如果选择的$l \gt d$，深度受限搜索同样也不是最优的。
• 时间复杂度：$O(b^l)$
• 空间复杂度：$O(bl)$

深度优先搜索可以看作是特殊的深度受限搜索，其深度$l = \infty$

迭代深入搜索iterative deepening

结合DFS的空间优势和BFS的时间优势

• 首先限制深度为1，进行深度优先搜索
• 然后限制深度为2，进行深度优先搜索
• 然后限制深度为3，进行深度优先搜索
• ……
• 当深度界限达到$d$，即最浅的目标结点所在深度时，就能找到目标结点。

浪费冗余：通常绝大多数的节点都在底层，所以上层节点生成多次影响不是很大

• 完备性：和宽度优先搜索一样，当分支因子有限时是该搜索算法是完备的
• 最优性：当路径代价是结点深度的非递减函数时该算法是最优的。
• 时间复杂度：$O(b^d)$
• 空间复杂度：$O(bd)$

双向搜索

同时运行两个搜索，一个从初始状态向前搜索同时另一个从目标状态向后搜索，希望它们在中间某点相遇，此时搜索终止。理由是$b^{d/2} + b^{d/2}$要比$b^d$小很多。

• 时间复杂度：$O(b^{\frac{d}{2}})$
• 空间复杂度：$O(b^{\frac{d}{2}})$

一般来讲，当搜索空间较大并且不知道解所在深度时，迭代加深的深度优先搜索是首选的无信息搜索方法。

搜索算法总结

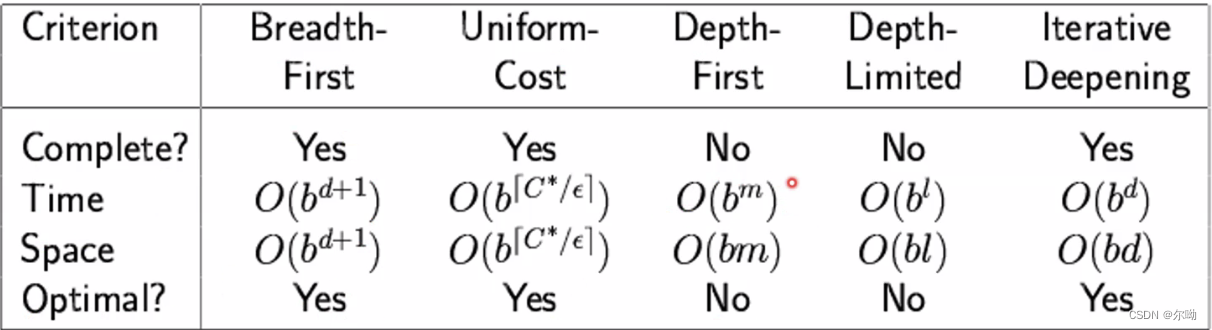
b表示树的宽度，是分支因子，m表示最大深度，d表示最浅目标节点的深度

有信息(启发式)的搜索策略informed search

使用问题本身的定义之外的特定知识，比无信息的搜索策略更有效地进行问题求解。
结点是基于评价函数$f(n)$值被选择扩展的。评估函数被看作是代价估计，因此评估值最低的结点被选择首先进行扩展。最佳优先图搜索的实现与一致代价搜索类似, 不过最佳优先是根据$f$值而不是$g$值对优先级队列排队。
对$f$的选择决定了搜索策略，大多数的最佳优先搜索算法$f$由启发函数(heuristic function) 构成:

$$h(n) = 结点n到目标结点的最小代价路径的代价估计值$$

• 估计一个状态到目标距离的函数
• 问题给予算法的额外信息，为特定搜索问题而设计

贪婪最佳优先搜索

• 策略：扩展最接近目标状态的节点，理由是这样可能可以很快找到解。因此，它只用启发式信息，即$f(n) = h(n)$，例如在罗马尼亚问题中是到目的地的距离。
• 通常情况下可以很快到达目标
• 最坏情况下类似于深度优先搜索
• 完备性：和深度优先搜索类似，不完备
• 最优性：不具备
• 时间复杂度：最坏情况下$O(b^m)$
• 空间复杂度：最坏情况下$O(b^m)$
• 复杂度决定于启发式函数的质量

$A^*$搜索

• 结合使用代价一致搜索(代价$g(n)$)和贪心搜索(代价$h(n)$)，$g(n)$是从开始结点到结点$n$的路径代价，$h(n)$是从结点 $n$ 到目标结点的最小代价路径的估计值

$$f(n) = d(n) + h(n)$$

• 算法和一致代价类似，只是使用的代价变为$f$
• 保证最优性的条件：可采纳性和一致性
• 一致的启发式都是可采纳的
• 如果$h(n)$是可采纳的，那么$A^*$的树搜索版本是最优的
• 如果$h(n)$是一致的，你们图搜索的$A^*$算法是最优的
  算法的结束条件：当目标入列时不停止，只有当目标出列时才停止

可采纳启发式

保障最优性的第一个条件是$h(n)$是一个可采纳启发式。可采纳启发式是指它从不会过高估计到达目标的代价。因为$g(n)$是当前路径到达结点$n$的实际代价，而$f(n) = g(n) + h(n)$，我们可以得到直接结论: $f(n)$永远不会超过经过结点$n$的解的实际代价。

• 启发函数h是可采纳的，那么：

$$0 \leq h(n) \leq h^*(n)$$

其中$h^*(n)$是最接近目标的真实耗散，例如到目标节点的直线距离肯定是最短的，那么当$h(n)$取直线距离的时候就是可采纳的

• 想出可采纳的启发函数是$A^*$算法实际使用中的重点

一致性启发式

对于每个节点$n$和通过任一行动$a$生成的$n$的每个后继结点$n'$，从结点$n$到达目标的估计代价不大于从$n$到$n'$的单步代价与从$n'$到达目标的估计代价之和

$$h(n) \leq c(n,a,n') + h(n')$$

$A^*$算法的最优性

• 首先证明如果$h(n)$是一致的，那么沿着任何路径的$f(n)$值是非递减的，假设有$n'$是$n$的后继结点，那么有：

$$f(n') = g(n') + h(h') = g(n) + c(n,a,n') + h(n') \geq g(n) + h(n) = f(n)$$

• 下一步则需要证明:若$A^*$选择扩展结点$n$时，就已经找到到达结点$n$的最优路径。否则，在到达结点$n$的最优路径上就会存在另一边缘结点$n'$，因为$f$在任何路径上都是非递减的，$n'$的$f$代价比$n$小，会先被选择。
• 所以算法以$f(n)$的非递减序扩展接点，所以第一个被选择扩展的目标结点一定是最优解，之后扩展的目标结点代价都不会低于它
• 算法是效率最优的，也就是说没有其他的最优算法可以保证扩展的结点数少于$A^*$算法

$A^*$算法的完备性

假设$C^*$是最优解路径的代价值，那么可以得到：

• $A^*$算法扩展所有$f(n) \lt C^*$的结点；
• 算法在扩展目标结点之前可能会扩展一些正好处于等值线$f(n) = C^*$上的结点，这要这样的结点的数目是有穷的，算法就是完备的

$A^*$算法的目标损耗

假设绝对误差定义为$\Delta \equiv h^* - h$，$h^*$表示从根结点到目标结点的实际代价，相对误差定义为$\varepsilon = (h^* - h) / h^*$，当模型是一个只有一个目标状态的状态空间时，时间复杂度为$O(b^\Delta)$，考虑每步骤代价均为常量，我们可以把这记为$O(b^{\varepsilon d})$

存储受限的启发式搜索

$A^*$算法减少内存需求的简单办法就是将迭代加深的思想用在启发式搜索上，即迭代加深$A^*(IDA^*)$算法

判断启发式函数的好坏

• 有效分支因子$b^*$，对于某一问题，如果$A^*$算法生成的总结点数为$N$，解的深度为$d$，那么$b^*$就是深度为$d$的标准搜索树为了能够包括$N + 1$个结点所必需的分支因子。即：

$$N + 1 = 1 + b^* + (b^*)^2 + \cdots + (b^*)^d$$

有效分支因子越小，启发式函数越好，设计良好的启发式会使$b^*$的值接近于1

• 对于两个启发式函数，如果对于任一结点$n$，有$h_2(n) \geq h_1(n)$，那么$h_2$启发式函数更好， 因为使用$h_2$的$A^*$算法永远不会比使用$h_1$的$A^*$算法扩展更多的结点

从松弛问题出发设计可采纳的启发式

• 减少了行动限制的问题称为松弛问题。松弛问题的状态空间图是原有状态空间的超图，原因是减少限制导致图中边的增加。
• 由于松弛问题增加了状态空间的边，原有问题中的任一最优解同样是松弛问题的最优解;但是松弛问题可能存在更好的解，理由是增加的边可能导致捷径。所以，一个松弛问题的最优解代价是原问题的可采纳的启发式。