[CSP-S 2021] 回文 题解

题目大意

现有一个整数序列 \(a_1, a_2, \ldots, a_{2n}\) ，在这 \(2n\) 个数中，\(1, 2, \ldots, n\) 分别各出现恰好 \(2\) 次。现在需要创建一个长度同样为 \(2n\) 的序列 \(b_1, b_2, \ldots, b_{2 n}\) ，初始时 \(b\) 为空序列，现在有两种操作：

1. 将序列 \(a\) 的开头元素加到 \(b\) 的末尾，并从 \(a\) 中移除。
2. 将序列 \(a\) 的末尾元素加到 \(b\) 的末尾，并从 \(a\) 中移除。

操作1用 L 表示，操作2用 R 表示，最终目的是让 \(b\) 成为一个回文数列 。如果可以达成目的，请输出字典序最小的操作方案；否则，输出 -1 。

分析

首先我们可以发现第1步操作只能选序列 \(a\) 最左边或最右边的元素，我们在此只讲诉第1步选最左边的元素的做法，而选最右边的与此同理，不再过多赘述。
我们可以发现，如果先选 \(a_1\) ，那么序列 \(a\) 中的有且仅有的另外一个 \(a_i=a_1\) 一定是在最后选。对于剩下的元素，进行如下两种操作：

• 将 \(a_i\) 左边的元素从左至右按从上到下的顺序放进栈 \(lsta\) 中。
• 将 \(a_i\) 右边的元素从右至左按从上到下的顺序放进栈 \(rsta\) 中。

现在问题便转化为了：

每次从栈 \(lsta\) 或栈 \(rsta\)的栈顶中取出一个元素放入序列 \(b\) 的末尾，最后使序列 \(b\) 成为一个回文序列，并让操作序列字典序最小。做法如下（此时的栈可以看作双端队列）：

1.对于栈 \(lsta\) 的栈顶，如果栈 \(lsta\) 或栈 \(rsta\) 的栈底有与其相同的元素，则删去这两个元素，并记录操作序列，跳过操作2（这是为了保证操作序列字典序最小，因为 L 字典序小于 R ）。
2.对于栈 \(rsta\) 的栈顶，如果栈 \(lsta\) 或栈 \(rsta\) 的栈底有与其相同的元素，则删去这两个元素，并记录操作序列。
3.如果上述操作均不能满足，则输出 -1 ；否则，循环进行上诉操作直至所有栈弹空。

举个例子：

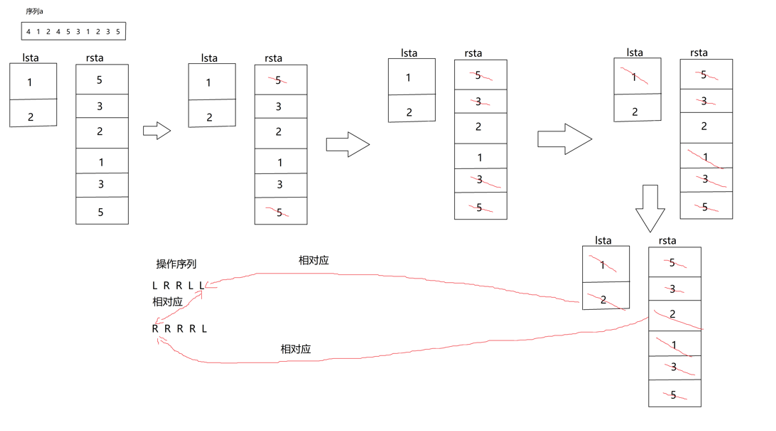
代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e5+5;
int t; 
int n;
int a[2*N],lsta[2*N],rsta[2*N];
int lbj,bj,rbj;
char ans[2*N];
int lfront,lback,rfront,rback,lans,rans;
int pd(){
	while(lans<rans){
		if(lfront>lback){
			if(rfront>=rback){
				bj=1;
				break;
			}
			if(rsta[rfront]==rsta[rback]){
				ans[lans++]='R';
				ans[rans--]='R';
				rfront++;
				rback--;
			}
			else{
				bj=1;
				break;
			}
		}
		else if(lfront==lback){
			if(rfront>rback){
				bj=1;
				break;
			}
			if(rfront==rback){
				if(lsta[lfront]==rsta[rfront]){
					ans[lans++]='L';
					ans[rans--]='R';
					lfront++;
					rfront++;
				}
				else{
					bj=1;
					break;
				}
			}
			else{
				if(lsta[lfront]==rsta[rback]){
					ans[lans++]='L';
					ans[rans--]='R';
					lfront++;
					rback--;
				}
				else if(rsta[rfront]==rsta[rback]){
					ans[lans++]='R';
					ans[rans--]='R';
					rfront++;
					rback--;
				}
				else if(lsta[lfront]==rsta[rfront]){
					ans[lans++]='R';
					ans[rans--]='L';
					lfront++;
					rfront++;
				}
				else{
					bj=1;
					break;
				}
			}
		}
		else{
			if(rfront>rback){
				if(lsta[lfront]==lsta[lback]){
					ans[lans++]='L';
					ans[rans--]='L';
					lfront++;
					lback--;
				}
				else{
					bj=1;
					break;
				}
			}
			else if(rfront==rback){
				if(lsta[lfront]==rsta[rback]){
					ans[lans++]='L';
					ans[rans--]='R';
					lfront++;
					rback--;
				}
				else if(lsta[lfront]==lsta[lback]){
					ans[lans++]='L';
					ans[rans--]='L';
					lfront++;
					lback--;
				}
				else if(lsta[lback]==rsta[rfront]){
					ans[lans++]='R';
					ans[rans--]='L';
					lback--;
					rfront++;
				}
				else{
					bj=1;
					break;
				}
			}
			else{
				if(lsta[lfront]==rsta[rback]){
					ans[lans++]='L';
					ans[rans--]='R';
					rback--;
					lfront++;
				}
				else if(lsta[lfront]==lsta[lback]){
					ans[lans++]='L';
					ans[rans--]='L';
					lback--;
					lfront++;
				}
				else if(rsta[rfront]==rsta[rback]){
					ans[lans++]='R';
					ans[rans--]='R';
					rback--;
					rfront++;
				}
				else if(rsta[rfront]==lsta[lback]){
					ans[lans++]='R';
					ans[rans--]='L';
					lback--;
					rfront++;
				}
				else{
					bj=1;
					break;
				}
			}
		}
	}
	return bj;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d",&n);
		for(int i=1;i<=2*n;i++){
			scanf("%d",&a[i]);
		}
		for(int i=2;i<=2*n;i++){
			if(a[i]==a[1]){
				lbj=i;
				break;
			}
		}
		ans[1]='L';
		ans[2*n]='L';
		lfront=1,lback=0,rfront=1,rback=0,lans=2,rans=2*n-1;
		for(int i=2;i<lbj;i++){
			lsta[++lback]=a[i];
		}
		for(int i=2*n;i>lbj;i--){
			rsta[++rback]=a[i];
		}
		bj=0;
		pd();
		if(bj){
			for(int i=1;i<2*n;i++){
				if(a[i]==a[2*n]){
					rbj=i;
					break;
				}
			}
			ans[1]='R';
			ans[2*n]='L';
			lfront=1,lback=0,rfront=1,rback=0,lans=2,rans=2*n-1;
			for(int i=1;i<rbj;i++){
				lsta[++lback]=a[i];
			}
			for(int i=2*n-1;i>rbj;i--){
				rsta[++rback]=a[i];
			}
			bj=0;
			pd();
			if(!bj){
				for(int i=1;i<=2*n;i++){
					printf("%c",ans[i]);
				}
				printf("\n");
			}
			else{
				printf("-1\n");
			}
		}
		else{
			for(int i=1;i<=2*n;i++){
				printf("%c",ans[i]);
			}
			printf("\n");
		}
	}
	return 0;
}