从零构建一个支持扩展的二目计算器
从零构建一个支持扩展的二目计算器
你需要了解的前置知识
- 逆波兰后缀表达式
- 面向对象思想 -> 多态
- 快速幂 & 矩阵快速幂 ---扩展运算符时使用
构建计算规则
先思考计算时候我们需要注意的事项
- 运算符优先级
- 运算符在遇到数字之后的计算规则
考虑这两项,如果将规则直接写到具体的计算代码中就会导致代码无法扩展,而这洽洽违背了面向对象设计,综合考虑,新增一个规则接口。
package core;
import java.math.BigDecimal;
import java.security.InvalidParameterException;
/**
* 计算规则接口
*/
public interface CalculatorRule {
/**
* 计算接口
* @param val1 双目表达式左值
* @param val2 双目表达式右值
* @return 计算结果
* @throws InvalidParameterException 规定参数无法解析时,抛出该异常
*/
BigDecimal method(String val1, String val2) throws InvalidParameterException;
/**
* 获取该运算符的优先级
* @return 优先级
*/
int priority();
}
构建基础计算器
基础的计算机中包含以下功能
- 添加运算符规则集合,若已存在该运算符则覆盖原来的规则 -> addOrReplaceAllCalculatorRule
- 添加运算符规则集合,若已存在该运算符则跳过 -> addAllCalculatorRule
- 添加单个运算符规则,若已存在该运算符则覆盖原来的规则 ->addOrReplaceCalculatorRule
- 添加单个运算符规则,若已存在该运算符则跳过 -> addCalculatorRule
- 获取运算符优先级 -> getPriority
- 获取逆波兰后缀表达式 -> reversePolishNotation
- 获取表达式计算结果 -> getResult
- 计算规则 -> calculation
- 逆波兰后缀表达式转换核心 -> manageOperator
- 分解原始表达式 -> decompositionFormula
- 判断字符串是否是当前所支持的数字 -> isSupportNumber
- 判断字符串是否是当前所支持的运算符 -> isSupportOperator
package core;
import java.math.BigDecimal;
import java.math.RoundingMode;
import java.security.InvalidParameterException;
import java.util.*;
/**
* 支持双目运算规则的基础计算类
*/
public class Calculators {
Map<String, CalculatorRule> rule = new HashMap<>();
/**
* 无参构造函数
*/
public Calculators(){
}
/**
* 在初始化时,添加计算规则
* @param rule 规则映射
*/
public Calculators(Map<String, CalculatorRule> rule){
this();
this.rule.putAll(rule);
}
/**
* 添加一个规则Map, 其中Key为定义的运算符, value为定义的接口
* @param rules 规则映射表
*/
public void addOrReplaceAllCalculatorRule(Map<String, ? extends CalculatorRule> rules){
this.rule.putAll(rules);
}
/**
* 添加一个规则Map, Key为定义的运算符, value为定义的接口
* @param rules 规则映射表
*/
public void addAllCalculatorRule(Map<String, ? extends CalculatorRule> rules){
Set<String> keySet = rules.keySet();
for (String item : keySet) {
assert rules.get(item) != null;
if (this.rule.containsKey(item)){
rules.remove(item);
keySet.remove(item);
}
}
this.rule.putAll(rules);
}
/**
* 添加一个规则Map, Key为定义的运算符, value为定义的接口
* @param operator 操作符
* @param rule 规则映射表
*/
public void addCalculatorRule(String operator, CalculatorRule rule){
if (this.rule.containsKey(operator)){
return;
}
this.rule.put(operator, rule);
}
public void addOrReplaceCalculatorRule(String operator, CalculatorRule rule){
this.rule.put(operator, rule);
}
/**
* 获取优先级
* @param op1 操作符1
* @param op2 操作符2
* @return 优先级
* @throws InvalidParameterException 在无法解析操作符时抛出无效参数异常
*/
public boolean getPriority(String op1, String op2) throws InvalidParameterException{
if (isSupportOperator(op1) && isSupportOperator(op2)){
return rule.get(op1).priority() > rule.get(op2).priority();
}
throw new InvalidParameterException(String.format("Invalid parameter %s %s", op1, op2));
}
/**
* 计算逆波兰表达式
* @param expression 基础表达式
* @return 逆波兰表达式元素集合
* @throws InvalidParameterException 在无法解析表达式时抛出无效参数异常
*/
public List<String> reversePolishNotation(String expression) throws InvalidParameterException {
List<String> initial = decompositionFormula(expression);
return reversePolishNotation(initial);
}
/**
* 获取表达式计算结果
* @param expression 表达式
* @return 表达式计算结果
* @throws InvalidParameterException 若表达式是无法解析的将会抛出该异常
*/
public BigDecimal getResult(String expression) throws InvalidParameterException {
return getResult(reversePolishNotation(expression));
}
/**
* 获取逆波兰表达式的计算结果
* @param reversePolishExpression 逆波兰表达式
* @return 逆波兰表达式计算结果
* @throws InvalidParameterException 若逆波兰表达式是无法解析的将会抛出该异常
*/
public BigDecimal getResult(List<String> reversePolishExpression) throws InvalidParameterException{
Stack<String> opera = new Stack<>();
for (String item : reversePolishExpression) {
if (isSupportNumber(item)){
opera.push(item);
}else if (isSupportOperator(item)){
opera.push(String.valueOf(calculation(opera.pop(), opera.pop(), item)));
}else {
throw new InvalidParameterException(reversePolishExpression.toString());
}
}
return new BigDecimal(opera.pop()).stripTrailingZeros();
}
/**
* 计算规则
* @param s1 双目右值
* @param s2 双目左值
* @param s3 运算符
* @return 结果
*/
public BigDecimal calculation(String s1, String s2, String s3) {
return rule.get(s3).method(s2, s1);
}
/**
* 通过已分解的表达式求逆波兰表达式
* @param expression 初始表达式
* @return 逆波兰式
* @throws InvalidParameterException 若表达式元素集合无法被解析,这将会触发无效参数异常
*/
public List<String> reversePolishNotation(List<String> expression) throws InvalidParameterException {
List<String> reversePolishExpression = new ArrayList<>();
Stack<String> operatorsStack = new Stack<>();
for (String item : expression) {
if (isSupportNumber(item)){
reversePolishExpression.add(item);
}else if (isSupportOperator(item)){
manageOperator(operatorsStack, reversePolishExpression, item);
}else {
throw new InvalidParameterException(expression.toString());
}
}
while (!operatorsStack.isEmpty()) {
reversePolishExpression.add(operatorsStack.pop());
}
return reversePolishExpression;
}
/**
* 计算逆波兰表达式核心
* @param operatorsStack 操作符栈
* @param reversePolishExpression 逆波兰式结果集合
* @param item 当前要处理的元素项
* @throws InvalidParameterException 若元素无法被处理则将抛出该异常
*/
private void manageOperator(Stack<String> operatorsStack, List<String> reversePolishExpression, String item) throws InvalidParameterException {
if (operatorsStack.isEmpty()){
operatorsStack.push(item);
}else if ("(".equals(item)){
operatorsStack.push(item);
}else if (")".equals(item)){
String string = "";
while (!operatorsStack.isEmpty() && !"(".equals(string = operatorsStack.pop())) {
reversePolishExpression.add(string);
}
}else if ("(".equals(operatorsStack.peek())) {
operatorsStack.push(item);
}
else if (getPriority(item, operatorsStack.peek())) {
operatorsStack.push(item);
}else {
reversePolishExpression.add(operatorsStack.pop());
manageOperator(operatorsStack, reversePolishExpression, item);
}
}
/**
* 分解表达式
* @param expression 初始表达式
* @return 分解后的表达式
*/
public List<String> decompositionFormula(String expression){
List<String> res = new ArrayList<>();
StringBuilder delim = new StringBuilder();
for (String s : rule.keySet()) {
delim.append(s);
}
StringTokenizer decomposition = new StringTokenizer(expression, delim.toString(), true);
while (decomposition.hasMoreTokens()) {
res.add(decomposition.nextToken());
}
return res;
}
/**
* 支持的操作运算符
* @param operator 运算符
* @return 是否支持
*/
public boolean isSupportOperator(String operator){
return rule.containsKey(operator);
}
/**
* 是不是支持运算的数字或小数
* @param number 数字/小数
* @return 是否支持
*/
public boolean isSupportNumber(String number){
return number.matches("([1-9]\\d*\\.?\\d*)|(0\\.\\d*[1-9])");
}
}
但是此时我们还不能用它来计算,因为该计算器中还没有运算符
构建基本四则运算
为了让我进行演示,所以我这里尝试构建四则运算,以此作为示例
将计算器的无参默认构造函数替换为如下代码即可
public Calculators(){
// 特殊字符右括号为内置
rule.put(")", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return null;
}
@Override
public int priority() {
return Integer.MIN_VALUE;
}
});
// 定义加法规则
rule.put("+", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return new BigDecimal(val1).add(new BigDecimal(val2));
}
@Override
public int priority() {
return 1;
}
});
// 定义减法规则
rule.put("-", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return new BigDecimal(val1).subtract(new BigDecimal(val2));
}
@Override
public int priority() {
return 1;
}
});
// 定义乘法规则
rule.put("*", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return new BigDecimal(val1).multiply(new BigDecimal(val2));
}
@Override
public int priority() {
return 2;
}
});
// 定义除法规则
rule.put("/", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return new BigDecimal(val1).divide(new BigDecimal(val2), 32, RoundingMode.DOWN);
}
@Override
public int priority() {
return 2;
}
});
// 特殊字符左括号为内置
rule.put("(", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return null;
}
@Override
public int priority() {
return Integer.MAX_VALUE;
}
});
}
尝试运行
尝试在main方法中运行它
public static void main(String[] args) throws InvalidParameterException {
Calculators calculators = new Calculators();
String expression = "34*(23-(1+23)*4-3.24)*(23-32*(23-324)/(34+34))/(43-45*343)";
List<String> strings = calculators.reversePolishNotation(expression);
StringBuilder stringBuilder = new StringBuilder();
for (String string : strings) {
stringBuilder.append(string);
}
System.out.println("初始化表达式: " + expression);
System.out.println("逆波兰表达式: " + stringBuilder.toString());
System.out.println("计算逆波兰式: " + calculators.getResult(strings));
// 这里只是为了方便看到转换的全过程,所以打印了以下输出等语句,实际使用过程中使用如下方式即可:
// Calculators calculators = new Calculators();
// String expression = "34*(23-(1+23)*4-3.24)*(23-32*(23-324)/(34+34))/(43-45*343)";
// System.out.println("计算结果: " + calculators.getResult(expression));
}
尝试运行它,你会得到以下结果:
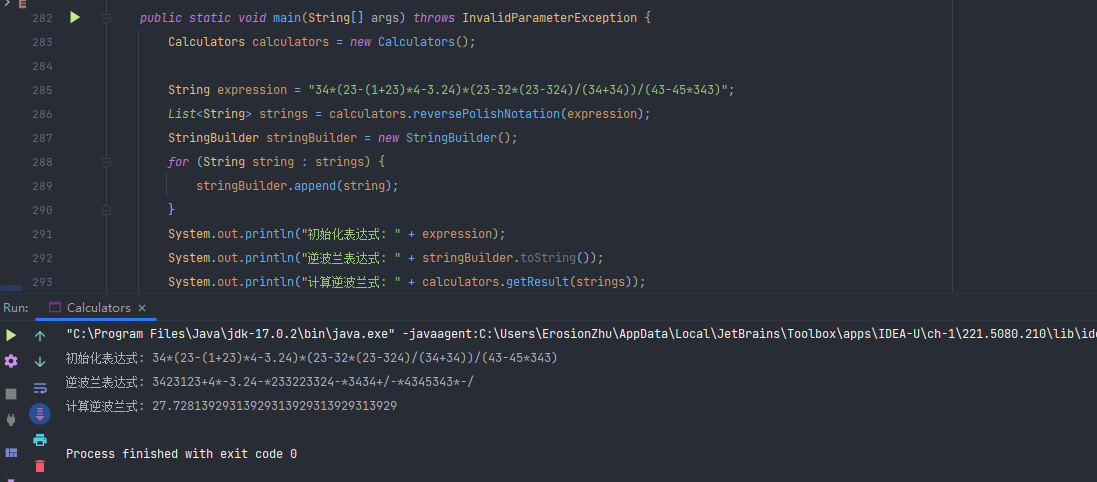
让我们来使用windows自带的计算器来验证我们是否是正确的
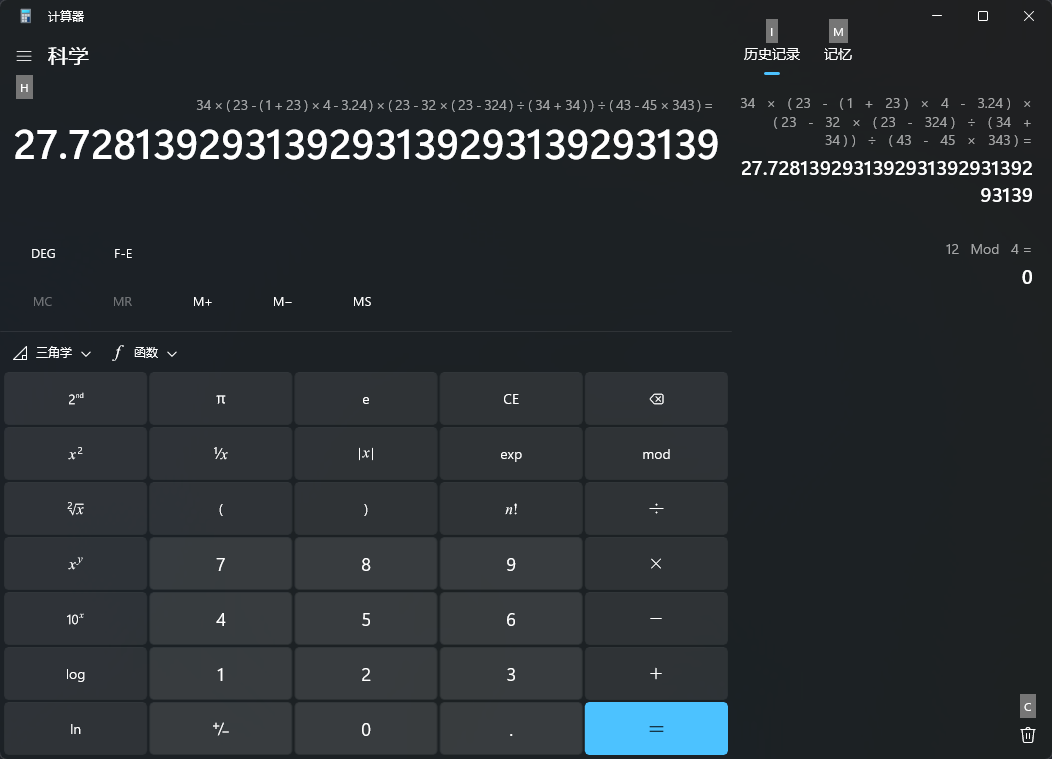
结果是完全正确的,只是windows自带的计算器保留了30位小数,而我的代码中保留了32位小数,这是在除法规则中规定的。
如果您不喜欢这么长的小数位,可以去修改它
尝试扩展简单运算符
现在我们的代码已经可以处理基本的四则运算了,但是还有一个求余运算符也是我们经常使用的,但是现在这个计算器还不具备这个功能,所以我们在外部来扩展它。
因为求余操作非常简单,所以直接实现该接口是一个非常简单的方式
public static void main(String[] args) throws InvalidParameterException {
Calculators calculators = new Calculators();
// ----------------------简单的扩展运算符例子-----------------------------
// 扩展后使得计算器支持求余操作
calculators.addOrReplaceCalculatorRule("%", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return new BigDecimal(val1).divideAndRemainder(new BigDecimal(val2))[1];
}
@Override
public int priority() {
return 2;
}
});
}
尝试运行
public static void main(String[] args) throws InvalidParameterException {
Calculators calculators = new Calculators();
// ----------------------简单的扩展运算符例子-----------------------------
// 扩展后使得计算器支持求余操作
calculators.addOrReplaceCalculatorRule("%", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return new BigDecimal(val1).divideAndRemainder(new BigDecimal(val2))[1];
}
@Override
public int priority() {
return 2;
}
});
// -------------------------尝试计算包含求余的表达式------------------------
String expression = "((34*(12%5)*3)*99)%21*3.1";
List<String> strings = calculators.reversePolishNotation(expression);
StringBuilder stringBuilder = new StringBuilder();
for (String string : strings) {
stringBuilder.append(string);
}
System.out.println("初始化表达式: " + expression);
System.out.println("逆波兰表达式: " + stringBuilder.toString());
System.out.println("计算逆波兰式: " + calculators.getResult(strings));
}
运行该例子,得到如下结果
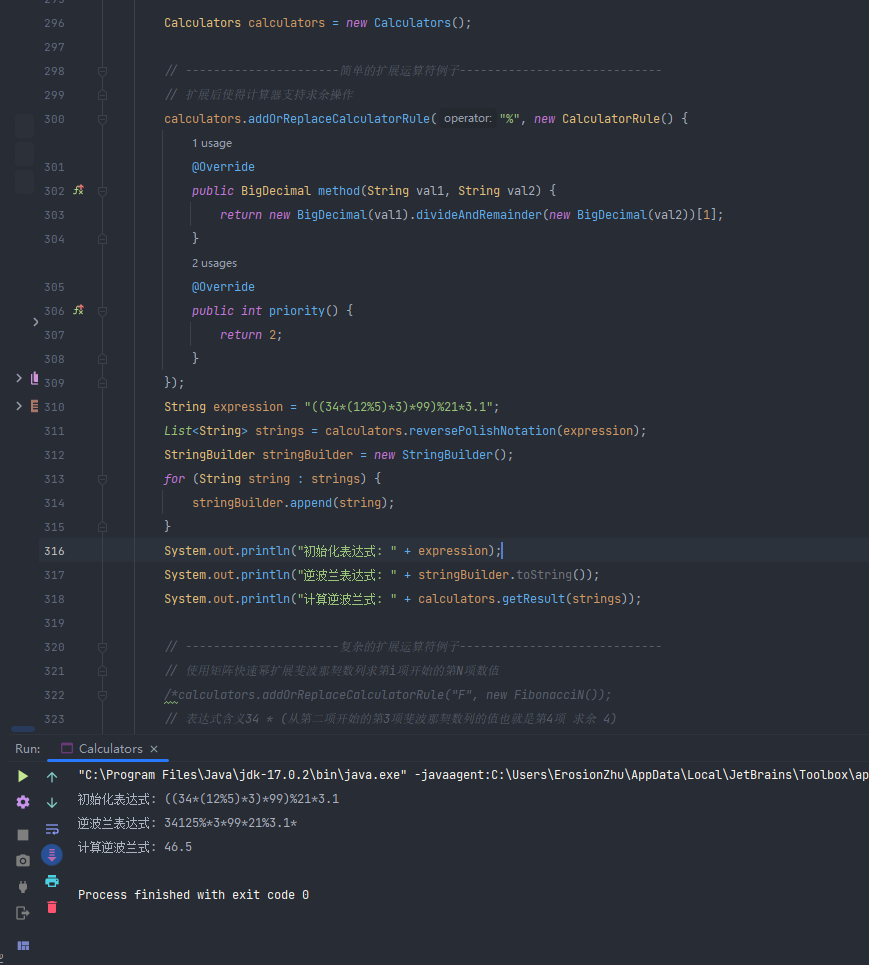
还是用windows计算器验证一下
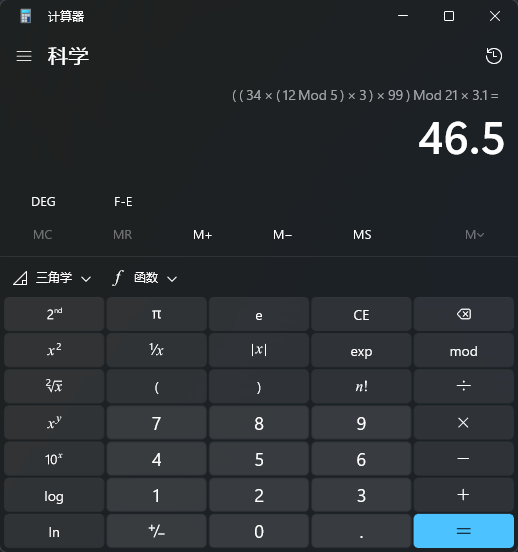
这就是简单的扩展操作符的简单例子
定义更加复杂的运算符
这里准备新增以下运算符,计算斐波那契数列的第N项,涉及到矩阵快速幂算法,不了解的同学可以去学习一下。
因为当前我们写的规则只适合双目运算,所以我这个规定了该运算符的使用方式是以F作为运算符,然后表达式左值为斐波那契数列的开始项,表达式右值为从开始项开始数的第N项数值,如:
3F5
// 该表达式的意思就是从斐波那契数列第三项开始数的第五项
// 总体来说就是斐波那契数列的第7项
0 1 1 2 3 5 [8] 13 21
// 结果就是方括号中的值
对于一些更加复杂的操作,我们直接去new一个接口就不合适了,因为这样会让我们的代码变的非常复杂
这里我们新建一个类,比如它叫FibonacciN 然后实现CalculatorRule接口并重写两个方法即可
package core;
import java.math.BigDecimal;
import java.security.InvalidParameterException;
public class FibonacciN implements CalculatorRule {
/**
* 定义2*2矩阵模型
*/
static class Matrix {
BigDecimal[][] source = new BigDecimal[2][2];
public Matrix(BigDecimal[][] other) {
if (other.length != this.source.length) {
throw new InvalidParameterException();
}
for (int x = 0; x < this.source.length; x++) {
System.arraycopy(other[x], 0, this.source[x], 0, this.source[x].length);
}
}
/**
* 矩阵相乘规则
*/
public Matrix multiply(Matrix other) {
if (other.source.length <= 0 || this.source.length <= 0 || other.source[0].length != this.source.length) {
throw new InvalidParameterException();
}
// 这里提前就知道这肯定是2*2矩阵相乘代码,但是最好还是不要去硬写,所以我这里写了通用的双矩阵相乘
BigDecimal[][] A = this.source;
BigDecimal[][] B = other.source;
BigDecimal[][] res = new BigDecimal[A.length][B[0].length];
for (int x = 0; x < A.length; x++) {
for (int y = 0; y < A[x].length; y++) {
res[x][y] = new BigDecimal(0);
for (int k = 0; k < B.length; k++) {
res[x][y] = res[x][y].add(A[x][k].multiply(B[k][y]));
}
}
}
return new Matrix(res);
}
/**
* 矩阵快速幂
* @param matrix 矩阵
* @param N 第N项
* @return 矩阵幂结果
*/
private Matrix MatrixQuickPow(Matrix matrix, int N) {
Matrix res = new Matrix(new BigDecimal[][]{
{new BigDecimal(1), new BigDecimal(0)},
{new BigDecimal(0), new BigDecimal(1)}
});
while (N > 0) {
if ((N & 1) == 1) {
res = res.multiply(matrix);
}
matrix = matrix.multiply(matrix);
N >>= 1;
}
return res;
}
}
/**
* 双目计算规则
* @param val1 双目左值
* @param val2 双目右值
* @return 表达式的值
* @throws InvalidParameterException 抛出可能的无效参数异常
*/
@Override
public BigDecimal method(String val1, String val2) throws InvalidParameterException {
int start = 0;
int N = 0;
try {
start = Integer.parseInt(val1);
N = start + Integer.parseInt(val2);
if (start <= 0 || N <= 0){
throw new InvalidParameterException();
}
} catch (NumberFormatException exception) {
throw new InvalidParameterException();
}
Matrix res = new Matrix(new BigDecimal[][]{
{new BigDecimal(0), new BigDecimal(1)},
{new BigDecimal(1), new BigDecimal(1)}
});
res = res.MatrixQuickPow(res, N);
return res.source[0][0];
}
/**
* 这里定义这个符号比乘除优先级更高,这样就能先计算该算式的结果了
* @return 优先级
*/
@Override
public int priority() {
return 3;
}
}
尝试运行
public static void main(String[] args) throws InvalidParameterException {
Calculators calculators = new Calculators();
// 扩展后使得计算器支持求余操作
calculators.addOrReplaceCalculatorRule("%", new CalculatorRule() {
@Override
public BigDecimal method(String val1, String val2) {
return new BigDecimal(val1).divideAndRemainder(new BigDecimal(val2))[1];
}
@Override
public int priority() {
return 2;
}
});
// ----------------------复杂的扩展运算符例子-----------------------------
// 使用矩阵快速幂扩展斐波那契数列求第i项开始的第N项数值
calculators.addOrReplaceCalculatorRule("F", new FibonacciN());
// 表达式含义34 * (从第二项开始的第3项斐波那契数列的值也就是第4项 求余 4)
String expression = "34*(3F5%5)*1.9";
List<String> strings = calculators.reversePolishNotation(expression);
StringBuilder stringBuilder = new StringBuilder();
for (String string : strings) {
stringBuilder.append(string);
}
System.out.println("初始化表达式: " + expression);
System.out.println("逆波兰表达式: " + stringBuilder.toString());
System.out.println("计算逆波兰式: " + calculators.getResult(strings));
}
尝试运行定义了斐波那契数列运算符的例子
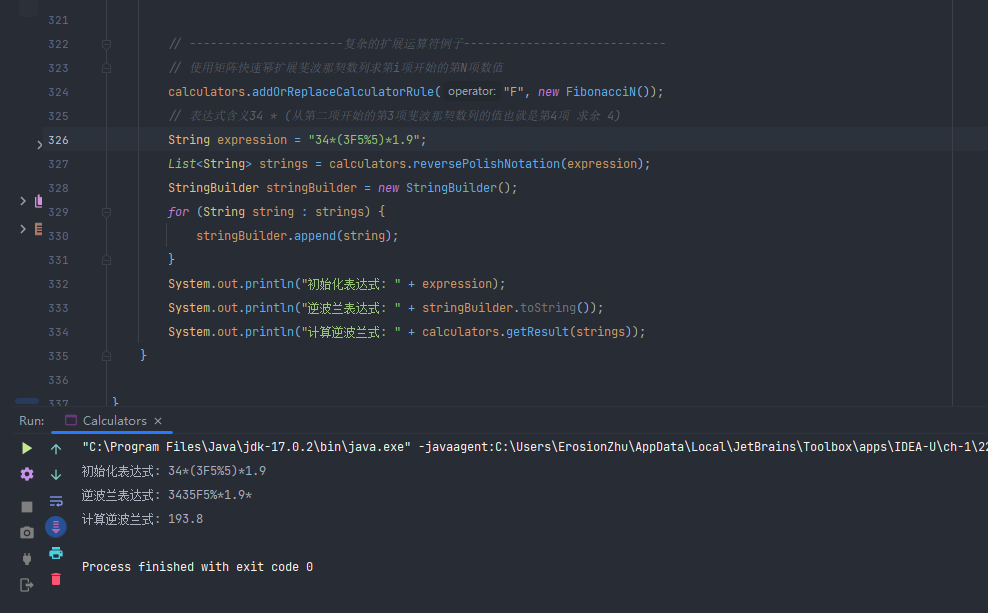
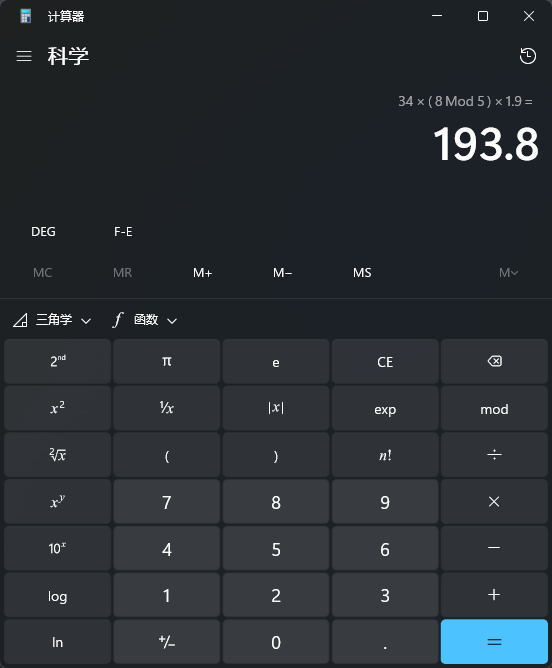
因为我们知道斐波那契数列第7项,所以这里验证的时候先把值写死就好了!
如果您对这份代码有什么问题或疑问,记得给我反馈哦,感谢~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号