LeetCode96 不同的二叉搜索树

题目

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。
二叉搜索树定义：
二叉搜索树是一种节点值之间具有一定数量级次序的二叉树，对于树中每个节点：
若其左子树存在，则其左子树中每个节点的值都不大于该节点值；
若其右子树存在，则其右子树中每个节点的值都不小于该节点值。

示例 1：
输入：n = 3
输出：5
示例 2：
输入：n = 1
输出：1

提示：
1 <= n <= 19

方法

动态规划法

G(n): 长度为 n 的序列能构成的不同二叉搜索树的个数。
F(i, n): 以 i 为根、序列长度为 n 的不同二叉搜索树个数(1≤i≤n)。i左边有i-个数，右边有n-i个数，所以F(i,n)=G(i−1)⋅G(n−i)
G(n)= ∑ F(i,n)（0<=i<=n）
因此G(n)= ∑ G(i−1)⋅G(n−i)（0<=i<=n）

• 时间复杂度：O（n2）
• 空间复杂度：O（n）

class Solution {
    public int numTrees(int n) {
        int[] g = new int[n+1];
        g[0] = 1;
        g[1] = 1;
        for(int i=2;i<=n;i++){
            for(int j=1;j<=i;j++){
                g[i] += g[j-1]*g[i-j];
            }   
        }
        return g[n];
    }
}

数学法

动态规划法中推导出的公式叫卡塔兰数 ：

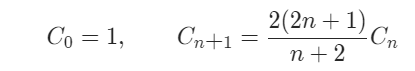
• 时间复杂度：O（n）
• 空间复杂度：O（1）

class Solution {
    public int numTrees(int n) {
        // 提示：我们在这里需要用 long 类型防止计算过程中的溢出
        long C = 1;
        for (int i = 0; i < n; ++i) {
            C = C * 2 * (2 * i + 1) / (i + 2);
        }
        return (int) C;
    }
}