matplotlib绘图

matplotlib绘图

import matplotlib.pyplot as plt
import numpy as np

 

plt.plot()绘制线性图

• 绘制单条线形图

• 绘制多条线形图

• 设置坐标系的比例plt.figure(figsize=(a,b))

• 设置图例legend()

• 设置轴的标识

• 图例保存

  • fig = plt.figure()

  • plt.plot(x,y)

  • figure.savefig（）

• 曲线的样式和风格（自学）

#绘制单条线形图
x = np.array([1,2,3,4,5])
y = x + 3

​
plt.plot(x,y)#线性图

 

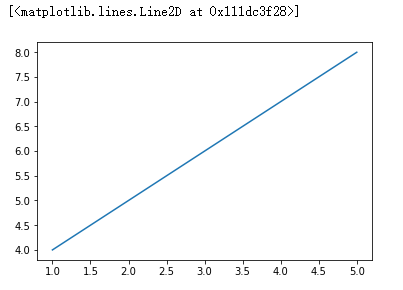
#绘制多条线形图
# 第一种方式
plt.plot(x,y)
plt.plot(x+1,y-2)

 

 

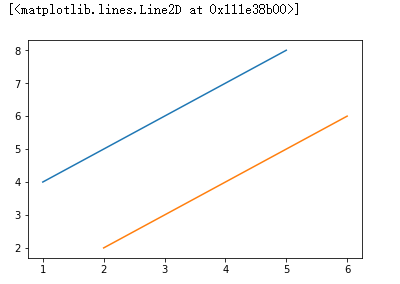
# 第二种方式
plt.plot(x,y,x+1,y-2)

 

 

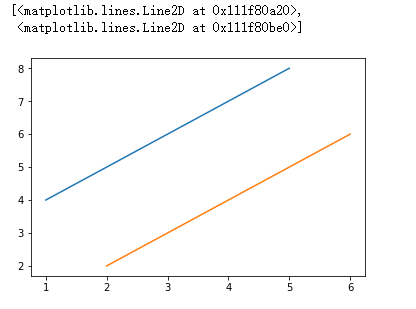
#设置坐标系的比例plt.figure(figsize=(a,b)) 将线型图等比例拉伸或缩小
plt.figure(figsize=(5,9))#放置在绘图的plot方法之前
plt.plot(x,y)

 

 

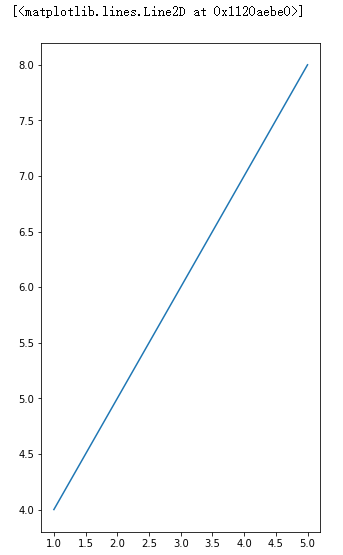
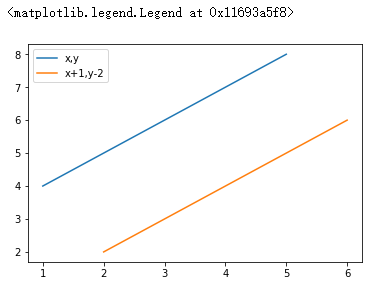
#设置图例legend()
plt.plot(x,y,label='x,y')
plt.plot(x+1,y-2,label='x+1,y-2')
plt.legend() #图例生效

 

 

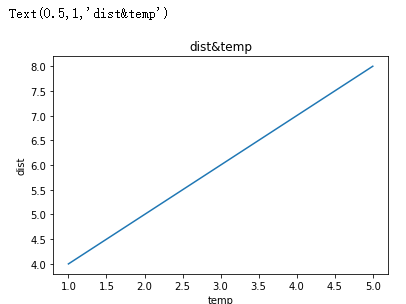
#设置轴的标识
plt.plot(x,y)
plt.xlabel('temp')
plt.ylabel('dist')
plt.title('dist&temp')

 

 

#图例保存
fig = plt.figure()  #对象实例化 该对象的创建一定要放置在plot绘图之前
plt.plot(x,y,label='x,y')# 绘图
fig.savefig('./123.png')# 保存 当前目录下./

 

 

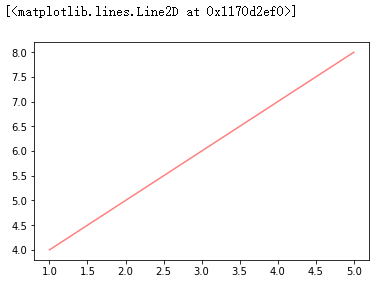
##曲线的样式和风格（自学）
plt.plot(x,y,c='red',alpha=0.5)

 

 

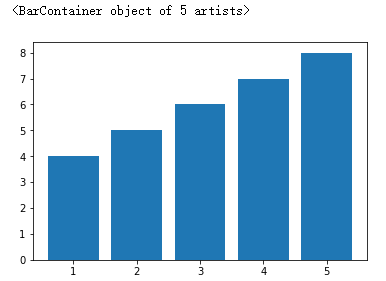
柱状图：plt.bar()

• 参数：第一个参数是索引。第二个参数是数据值。第三个参数是条形的宽度

plt.bar(x,y)

 

 

直方图

• 是一个特殊的柱状图，又叫做密度图

• plt.hist()的参数

  • bins 可以是一个bin数量的整数值，也可以是表示bin的一个序列。默认值为10

  • normed 如果值为True，直方图的值将进行归一化处理，形成概率密度，默认值为False

  • color 指定直方图的颜色。可以是单一颜色值或颜色的序列。如果指定了多个数据集合,例如DataFrame对象，颜色序列将会设置为相同的顺序。如果未指定，将会使用一个默认的线条颜色

  • orientation 通过设置orientation为horizontal创建水平直方图。默认值为vertical

 

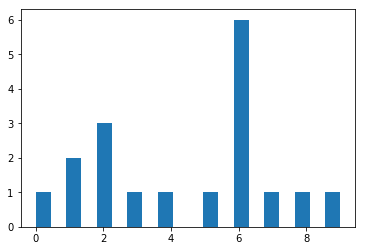
data = [1,1,2,2,2,3,4,5,6,6,6,6,6,6,7,8,9,0]
plt.hist(data,bins=20)#bins=20 20个柱子有的柱子高为0

(array([1., 0., 2., 0., 3., 0., 1., 0., 1., 0., 0., 1., 0., 6., 0., 1., 0.,
        1., 0., 1.]),
 array([0.  , 0.45, 0.9 , 1.35, 1.8 , 2.25, 2.7 , 3.15, 3.6 , 4.05, 4.5 ,
        4.95, 5.4 , 5.85, 6.3 , 6.75, 7.2 , 7.65, 8.1 , 8.55, 9.  ]),
 <a list of 20 Patch objects>)

 

 

 

饼图

• pie()，饼图也只有一个参数x

• 饼图适合展示各部分占总体的比例，条形图适合比较各部分的大小

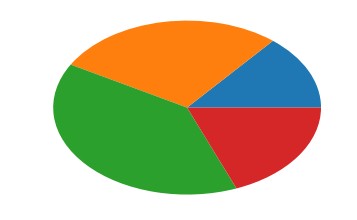
arr=[11,22,31,15]
plt.pie(arr)

([<matplotlib.patches.Wedge at 0x1178be1d0>,
  <matplotlib.patches.Wedge at 0x1178be6a0>,
  <matplotlib.patches.Wedge at 0x1178beb70>,
  <matplotlib.patches.Wedge at 0x1178c60f0>],
 [Text(0.996424,0.465981,''),
  Text(-0.195798,1.08243,''),
  Text(-0.830021,-0.721848,''),
  Text(0.910034,-0.61793,'')])

 

 

arr=[0.2,0.3,0.1]
plt.pie(arr)

([<matplotlib.patches.Wedge at 0x1177d0e80>,
  <matplotlib.patches.Wedge at 0x1177da390>,
  <matplotlib.patches.Wedge at 0x1177da8d0>],
 [Text(0.889919,0.646564,''),
  Text(-0.646564,0.889919,''),
  Text(-1.04616,-0.339919,'')])

 

 

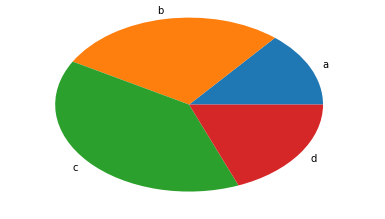
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'])

([<matplotlib.patches.Wedge at 0x11794aa90>,
  <matplotlib.patches.Wedge at 0x11794af60>,
  <matplotlib.patches.Wedge at 0x1179544e0>,
  <matplotlib.patches.Wedge at 0x117954a20>],
 [Text(0.996424,0.465981,'a'),
  Text(-0.195798,1.08243,'b'),
  Text(-0.830021,-0.721848,'c'),
  Text(0.910034,-0.61793,'d')])

 

 

 

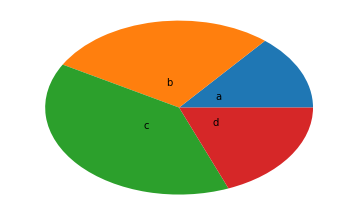
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'],labeldistance=0.3)

([<matplotlib.patches.Wedge at 0x1179e2278>,
  <matplotlib.patches.Wedge at 0x1179e2748>,
  <matplotlib.patches.Wedge at 0x1179e2c18>,
  <matplotlib.patches.Wedge at 0x1179eb198>],
 [Text(0.271752,0.127086,'a'),
  Text(-0.0533994,0.295209,'b'),
  Text(-0.226369,-0.196868,'c'),
  Text(0.248191,-0.168526,'d')])

 

 

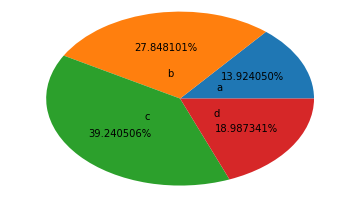
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'],labeldistance=0.3,autopct='%.6f%%')

([<matplotlib.patches.Wedge at 0x117a709e8>,
  <matplotlib.patches.Wedge at 0x117a7a128>,
  <matplotlib.patches.Wedge at 0x117a7a898>,
  <matplotlib.patches.Wedge at 0x117a83048>],
 [Text(0.271752,0.127086,'a'),
  Text(-0.0533994,0.295209,'b'),
  Text(-0.226369,-0.196868,'c'),
  Text(0.248191,-0.168526,'d')],
 [Text(0.543504,0.254171,'13.924050%'),
  Text(-0.106799,0.590419,'27.848101%'),
  Text(-0.452739,-0.393735,'39.240506%'),
  Text(0.496382,-0.337053,'18.987341%')])

 

 

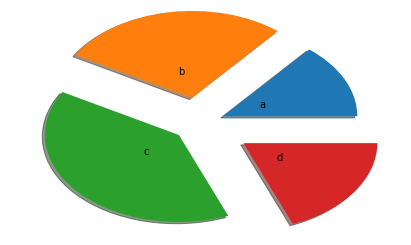
arr=[11,22,31,15]
plt.pie(arr,labels=['a','b','c','d'],labeldistance=0.3,shadow=True,explode=[0.2,0.3,0.2,0.4])

([<matplotlib.patches.Wedge at 0x117ab2390>,
  <matplotlib.patches.Wedge at 0x117ab2b38>,
  <matplotlib.patches.Wedge at 0x117abb390>,
  <matplotlib.patches.Wedge at 0x117abbba8>],
 [Text(0.45292,0.21181,'a'),
  Text(-0.106799,0.590419,'b'),
  Text(-0.377282,-0.328113,'c'),
  Text(0.579113,-0.393228,'d')])

 

 

 

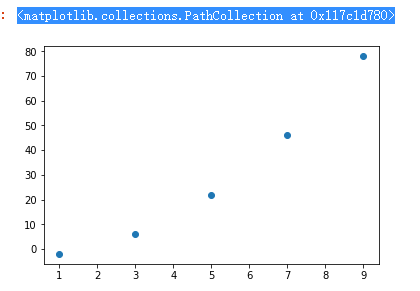
散点图scatter()

• 因变量随自变量而变化的大致趋势

x = np.array([1,3,5,7,9])
y = x ** 2 - 3
plt.scatter(x,y)

 

 

 

Type Markdown and LaTeX: 𝛼2α2

Type Markdown and LaTeX: 𝛼2α2

Type Markdown and LaTeX: 𝛼2