2024 ICPC ShaanXi Provincial Contest C. Seats&G. Disappearing Number

C. Seats

题目链接👈

题目描述🥰

题目思路😀

这个题目乍一看是二分图，实际上是一个基环森林

我们可以注意的：

• 有2n个点，2n条边，所以如果存在环的话，就只可能存在一个环。
• 因为一个点的出度只有1（不算自环的那个边），所以整个图相当于1/0个环+1/多个链

所以根据上面的观察，我们只需要计算每一个链的长度-1的贡献和加上环的大小即可

Tips

我们计算链的长度的时候，肯定是计算大于n的节点作为链的结尾（因为小于等于n的节点的出度一定不为0，无法成为链的节点。）

AC代码🧠

const int N=2e5+20,M=2*N;
int h[N],e[M],idx,ne[M];
void add(int a,int b)
{
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx++;
}
int n;
void solve()
{
	memset(h,-1,sizeof h);
	cin>>n;
	vector<int>to(2*n+1);
	for(int i=1;i<=n;i++)
	{
		int x;
		cin>>x;
		add(i,x);
		to[x]++;
	}
	queue<int>q;
    for(int i=1;i<=2*n;i++)
      if(!to[i])
    {
    	q.push(i);
    }
    vector<int>dist(2*n+1),vist(2*n+1);
    while(q.size())
    {
    	auto x=q.front();
    	q.pop();
    	vist[x]=1;
    	for(int i=h[x];~i;i=ne[i])
    	{
    		int j=e[i];
    		dist[j]=max(dist[j],dist[x]+1);
    		to[j]--;
    		if(to[j]==0)
    		{
    			q.push(j);
    		}
    	}
    }
    // for(int i=n+1;i<=2*n;i++)cout<<dist[i]<<" ";
    // cout<<endl;
    int ans=0;
    for(int i=1;i<=2*n;i++)
    {
    	//如果没有访问过，肯定是在环上面
    	if(vist[i]==0)ans++;
    	//加上以i位结尾的链的贡献
    	if(i>n)ans+=dist[i];
    }
    cout<<ans<<endl;
}

G. Disappearing Number

题目链接👈

题目描述🥰

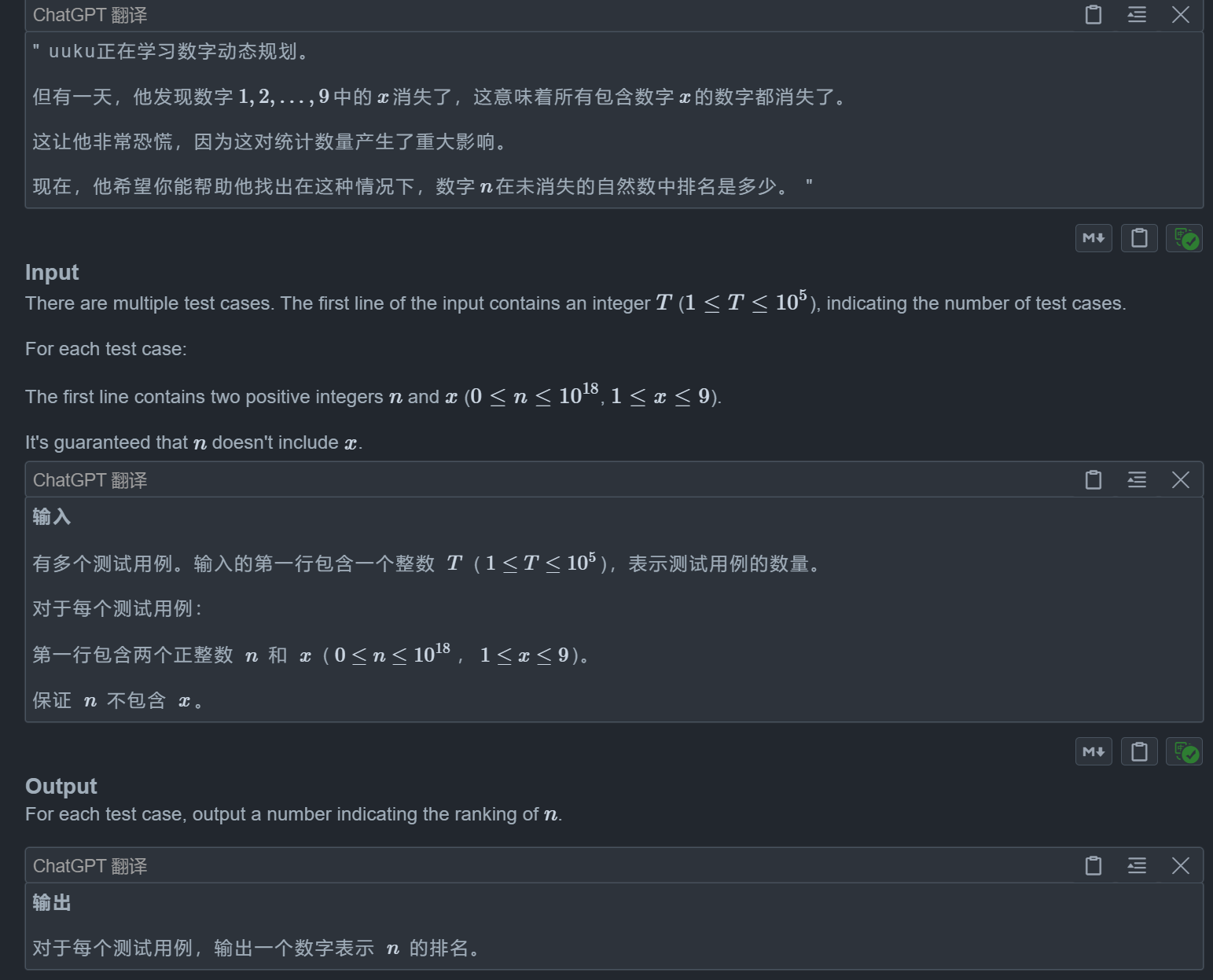
题目思路😀

赛事写的是数位DP，赛后看题解才发现自己是小丑🤡，题解提供了一个很妙的思路

我们可以先从特殊到一般

• 当k==9的情况下，实际上就是“逢九进一”，那么就是一个九进制，我们就可以直接把n这个九进制数转为十进制即可。
• 而k！=9的情况下，我们可以把n里面大于k的数位都减一（这个操作是不会改变数的顺序的），然后把处理过的n从九进制转为十进制即可。

思路出来了，代码也就很简单了🥰

Tips

我们的自然数是从0的开始的，所以最后的答案需要加1.

AC代码🧠

数位DP AC代码

int countNumbersWithoutX(int n, int x) {
  string s = to_string(n);
  int m = s.size();
  vector<vector<int>> memo(m, vector<int>(2, -1));

  auto dfs = [&](auto &&dfs, int i, bool is_limit, bool is_num) -> int {
    if (i == m) return is_num;
    if (!is_limit && is_num && memo[i][1] != -1) return memo[i][1];
    if (!is_limit && !is_num && memo[i][0] != -1) return memo[i][0];

    int res = 0;
    if (!is_num) res += dfs(dfs, i + 1, false, false);

    int up = is_limit ? s[i] - '0' : 9;
    for (int d = is_num ? 0 : 1; d <= up; ++d) {
      if (d == x) continue;
      res += dfs(dfs, i + 1, is_limit && (d == up), true);
    }

    if (!is_limit) memo[i][is_num] = res;
    return res;
  };

  return dfs(dfs, 0, true, false);
}

void solve() {
  int n, x;
  cin >> n >> x;
  int ans = countNumbersWithoutX(n, x);
  cout << ans + 1 << endl;
}

妙妙思路 AC代码

void solve()
{
	int n,x;
	cin>>n>>x;
	string s=to_string(n);
	if(x!=9)
	{
		for(auto &ch:s)
		{
			int k=ch-'0';
			if(k>x){
			  ch=(char)(k-1+'0');
			}
		}
	}
	reverse(s.begin(),s.end());
	int ans=0;
	for(int i=0;i<s.size();i++)ans+=pow(9,i)*(s[i]-'0');
	cout<<ans+1<<endl;
}