Codeforces Round 1017 (Div. 4) E&F题&H题

Codeforces Round 1017 (Div. 4)

E. Boneca Ambalabu

题目链接👈

题目描述🥰

题目思路😀

一个简单的思路就是拆位，最后答案就是每一位的按位异或的贡献之和。

我们可以先预处理一下每一位上的0和1的个数，然后枚举每一个元素ai，对于ai的每一数位进行枚举。

• 如果当前位为1，那么当前位的贡献就是其他元素中当前位为0的个数*当前位的权重；
• 而相应的，如果当前位为0，那么当前位的贡献就是其他元素中当前位为1的个数*当前位的权重。

代码也很简单

AC代码🧠

void solve()
{
	int n;
        cin >> n;
        vector<int> a(n);
        for (int i = 0; i< n; ++i)cin >> a[i];
        vector<vector<int>> res(30, vector<int>(2, 0));
        for (int x : a) {
            for (int i = 0; i < 30; i++) {
                if ((x >> i) & 1) {
                    res[i][1]++;
                }else {
                    res[i][0]++;
                }
            }
        }
       int  ans= 0;
        for (auto x : a) {
            int sum = 0;
            for (int i = 0; i < 30; i++) {
                if ((x >> i) & 1) {
                    sum += res[i][0] * (1LL << i);
                }else{
                    sum += res[i][1] * (1LL << i);
                }
            }
            ans=max(ans,sum);
        }
        cout << ans << endl;
}

F. Trulimero Trulicina

题目链接👈

题目描述🥰

题目思路😀

题目的意思很简单，就是构造一个矩阵，需要矩阵里面出现1~k个数，而且每一个数出现的频率相等。

一个按道理说很简单的构造题，但是赛时没有处理好逻辑问题坠机了😭

题解的思路很清晰了，就是考虑m和k的关系

• 如果m%k！=0的话，那么我们就直接递增式的填数字，像第二个样例一样（n=3,m=4,k=6），这样的填法相同的数字肯定是不会重复的。

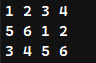
• 如果 m |  k  ，那么如果按上面的方式去填数字，肯定会有重复的情况(如n=4，m=6,k=3),这样相邻行会出现重复的情况

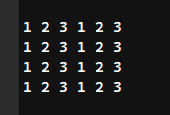
• 所以我们在m | k的情况下需要采取另外一种填数字的方式，我们可以采取构造里面经典技巧——shift
• 当我们填完第一行的时候，我们第二行可以向左shift一位，第三行和第一行一样，第四行和第二行一样，这样就可以实现相邻元素不一样的要求

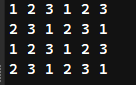
这个逻辑理清楚之后，我们的代码实现就很简单了😺

AC代码🧠

void solve()
{
	int n,m,k;
	cin>>n>>m>>k;
	if(m%k==0)
	{
	    for(int i=1;i<=n;i++)
	    {
	    	if(i&1)
	    	{
	    		int cnt=0;
	    		for(int j=1;j<=m;j++){
	    			cout<<(cnt%k)+1<<" ";
	    			cnt++;
	    		}
	    	}else{
	    		int cnt=1;
	    		for(int j=1;j<=m;j++){
	    			cout<<(cnt%k)+1<<" ";
	    			cnt++;
	    		}
	    	}
	    	cout<<endl;
	    }
	}else{
		int cnt=0;
		for(int i=1;i<=n;i++)
		{
		 for(int j=1;j<=m;j++)
		 {
		 	cout<<(cnt%k)+1<<" ";
		 	cnt++;
		 }
		 cout<<endl;
		}
	}
}

H. La Vaca Saturno Saturnita

题目链接👈

题目描述🥰

题目思路😀

这个题目最重要的就是对于数据的预处理，我们可以先预处理k范围里面的倍数，还需要预处理数组里面每一个元素，这样我们就可以查询每一个离当前下标最近的且是k的倍数的数组元素的下标。

预处理完数据，代码实现就很简单了

AC代码🧠

const int N=1e5+10;
vector<vector<int>>f(N);
void solve()
{
	 int n,q;
	 cin>>n>>q;
	 vector<int>a(n);
	 for(int i=0;i<n;i++)cin>>a[i];
	 //用hash表存储每一个元素的位置
	 map<int,vector<int>>hash;
	 for(int i=0;i<n;i++)hash[a[i]].push_back(i);
	 //这个函数是找到数组里面是k的因数的数的最近下标
	 auto find=[&](int x,int l)->int
	 {
	 	auto it=lower_bound(hash[x].begin(),hash[x].end(),l);
	 	if(it!=hash[x].end())return *it;
	 	return (int)1e9;
	 };
	 while(q--)
	 {
	 	int k,l,r;
	 	cin>>k>>l>>r;
	 	l--,r--;
	 	//记录当前的位置
	 	int curr=l;
	 	int ans=0;
	 	while(curr<=r)
	 	{
	 	   int mxr=r+1;
	 	   for(auto x:f[k])mxr=min(mxr,find(x,curr));
	 	   ans+=(mxr-curr)*k;
	 	   curr=mxr;
	 	   if(curr<=r)
	 	   {
	 	   	  while(k%a[curr]==0)k/=a[curr];
	 	   }
	 	}
	 	cout<<ans<<endl;
	 }
}

signed main()
{

    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    //预处理每一个数的倍数
	for(int i=1;i<=f.size();i++)
		for(int j=i;j<=f.size();j+=i)
			f[j].push_back(i);
	caseT
    solve();
    return 0;
}