Codeforces Round 960 (Div. 2) B C D题

B. Array Craft

题目链接👈

题目描述🥰

题目思路😀

我们可以发现两个条件

1.最大前缀后面的值之和不能大于0，

2. 最大后缀前面的值之和不能大于0

而最大前缀和最大后缀中间的值可以不需要管，我们可以把它们全赋值为1，然后再向两边扩展，同时需要满足前面的两个条件。

AC代码🧠

void solve()
{
	int n,x,y;
	cin>>n>>x>>y;
	vector<int>ans(n+1);
	for(int i=y;i<=x;i++)ans[i]=1;
	for(int i=y-1;i>=0;i--){
		if(ans[i+1]>0)ans[i]=-1;
		else ans[i]=1;
	}
	for(int i=x+1;i<=n;i++)
	{
		if(ans[i-1]>0)ans[i]=-1;
		else ans[i]=1;
	}
	for(int i=1;i<=n;i++)cout<<ans[i]<<" ";
	cout<<endl;
}

C. Boboniu and Bit Operations

题目链接👈

题目描述🥰

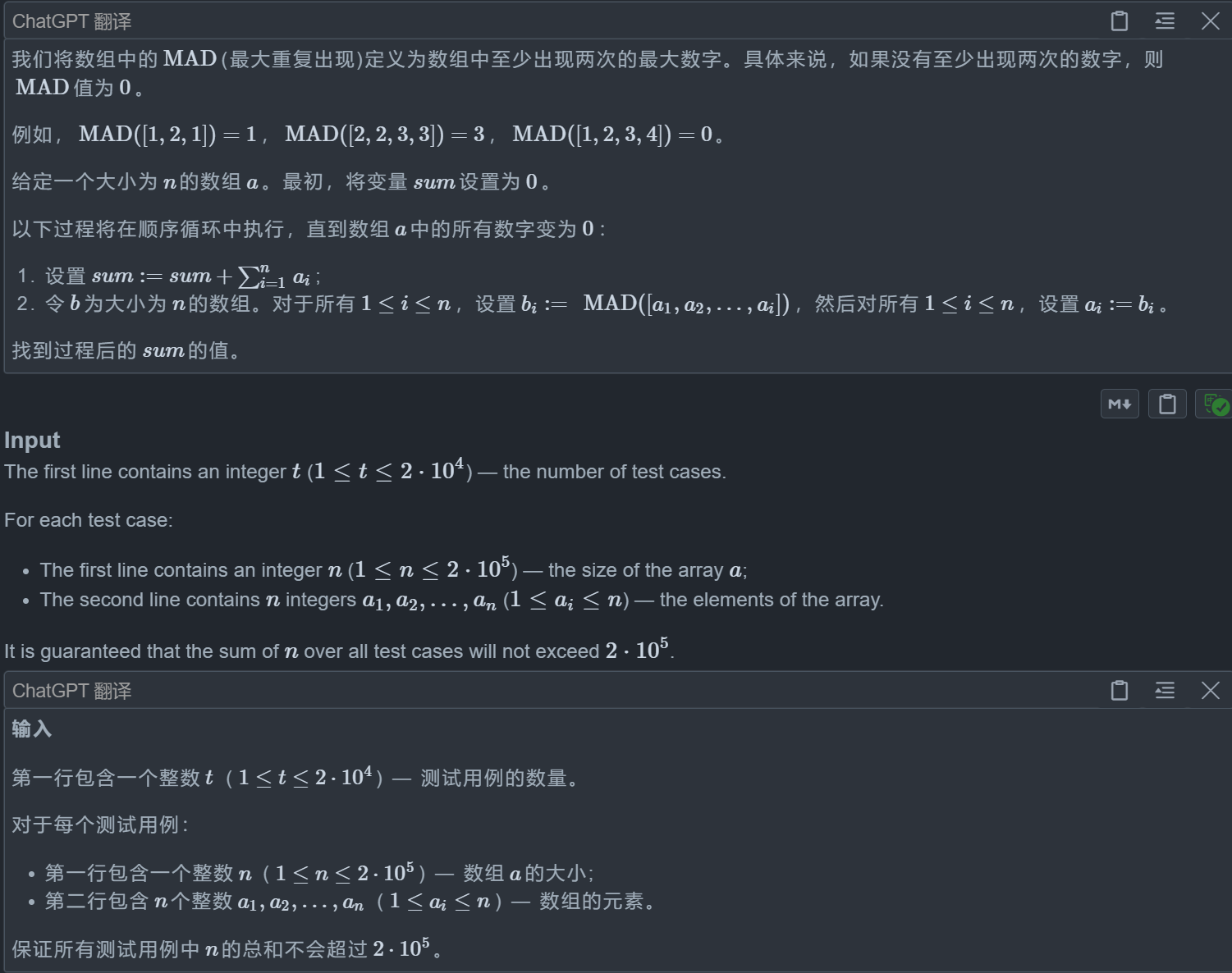
题目思路😀

首先我们需要去模拟这个过程，通过模拟了几组数据我们就可以发现这道就是计算数组里面每一个元素的贡献即可。

我们遍历数组，在遍历到第 i 个元素的元素之前出现过，这个元素就满足出现至少两次的条件，我们就可以把这个元素和res取max（res记录的是当前1~i数组里面的满足出现次数至少两次条件的最大数），如果这个最大值res在之前也出现过（但是这个res不能是0），我们就需要把这个res和tmp取最大值（tmp是后续（n-i）轮里面第 i 个元素的值）

综上所述，第 i 个元素的对ans的贡献是 这个元素本身 + res + (n-i）* tmp ,最后计算贡献之和就可以了

AC代码🧠

void solve()
{
	int n;
	cin>>n;
	map<int,int>hash,mp;
	int ans=0,res=0,tmp=0;
	for(int i=0;i<n;i++)
	{
		int x;
		cin>>x;
		//如果这个数之前出现过，就取当前的最大值
		if(hash[x])res=max(res,x);
		else  hash[x]++;
	    if(mp[res])tmp=max(tmp,res);
		else if(res) mp[res]++;
		ans+=x+res+(n-i)*tmp;
	}
	cout<<ans<<endl;
}

D. Grid Puzzle

题目链接👈

题目描述🥰

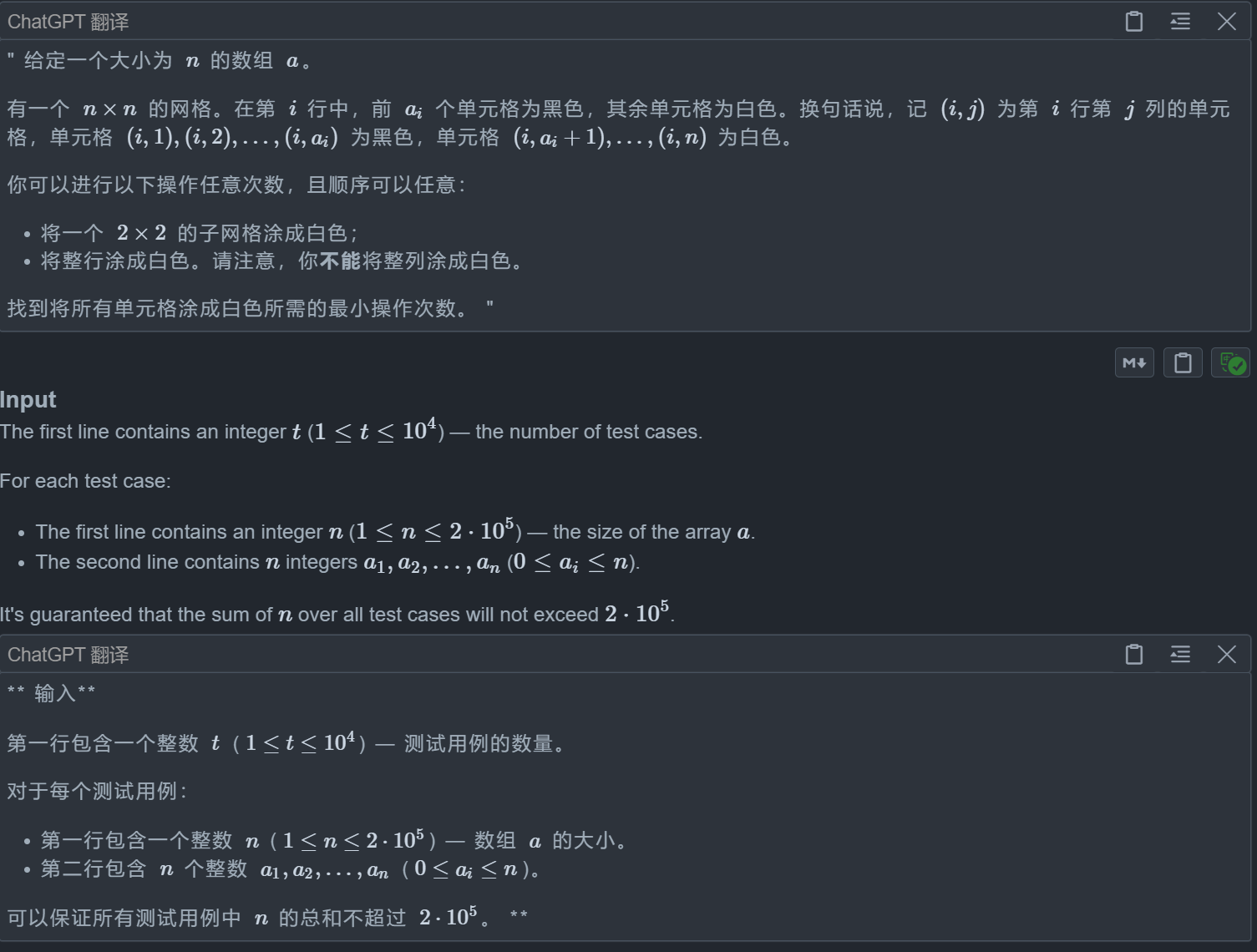
题目思路😀

这个题和它的rating不太相符（bushi）🤔，单纯1200左右的难度感觉

这个题目的关键是你需要注意到一种情况：当一个 ai > 4 ,我们就没有必要去用操作一来操作，因为我们用操作二更加划算，只需要一次就能够涂完这一行

而当一个ai>0&&ai<=2的时候，我们就可以贪心的使用操作一了，因为这个操作可以在涂完这一行的前提下可以填掉一些下一行的格子。

因为贪心的操作一的存在，所以我们的第i行会有两种可能：

1.ai的前两个格子被前面顺带涂了。

2.如果格子数ai>=4,那么可能第3和第四个格子被前面顺带涂了。

所以我们可以用两个数组来标记ai是否有这两种可能，并在涂第i行格子的时候对状态进行判断和标记。

AC代码🧠

void solve()
{
	int n;
	cin>>n;
	vector<int>a(n);
	for(int i=0;i<n;i++)cin>>a[i];
	vector<bool>st(n,false);//标记前两个格子有没有被涂
	vector<bool>k(n,false);//标记第3,4个格子有没有被涂
	int ans=0;
	for(int i=0;i<n-1;i++)
	{
		if(!st[i]&&a[i]<=2&&a[i]>0&&!k[i]){
			st[i+1]=true;
			a[i+1]-=2;
			ans++;
		}else if(k[i]&&a[i]<=2&&a[i]>0)
		{
			st[i+1]=true;
			a[i+1]-=2;
			ans++;
		}
		else if(st[i]&&a[i]<=2&&a[i]>0)
		{
			if(a[i+1]>2){
				k[i+1]=true;
				a[i+1]-=2;
			}
			ans++;
		}else if(a[i]>0) ans++;
	}
	if(a[n-1]>0)ans++;
	cout<<ans<<endl;
}