Codeforces Round #817 (Div. 4) D-F

https://codeforces.ml/contest/1722

D. Line

对于每次转换，在最边上转换总是最优。

左边的最优应该朝右，右边的最优应该朝左

不知道为什么编译不了，重新写一遍就编译过去了，但花了半小时才AC掉，中途还忘记设置数组范围而TLE了一发

//#define int ll
const int N = 2e5+10;
int n,m;
 
int a[N],ans[N];
int result[N];
void solve()
{
//    cin>>n>>m;
    cin>>n;
    string s;
    cin>>s;
    int len = s.size();
    s = " " + s;
    ll res = 0;
    fo(i,1,len) {
        if(s[i] == 'L') {
            res += i-1;
            a[i] = i - 1;
        } else {
            res += n-i;
            a[i] = n - i;
        }
    }
//    db(res);
//    gg
    int k = 0;
    
    fo(i,1,n) {
        if(i % 2 == 1) {
            int idx = i / 2 + 1;
//            db(idx);
            if(s[idx] == 'L') {
                k ++ ;
                res = res - a[idx] + (n - idx);
                cout<<res<<' ';
            }
        } else {
            int idx = n - i / 2 + 1;
//            db(idx);
            if(s[idx] == 'R') {
                k ++ ;
                res = res - a[idx] + (idx - 1);
                cout<<res<<' ';
            }
        }
    }
    k ++ ;
    while(k <= n) {
        cout<<res<<' '; 
        k ++ ;
    } cout<<endl;
}

E：二维树状数组区间和

 

 

 可以想象假如要中间这段区间的总和，直接把中间这一段都加起来就可以了

普通的二维区间和也可以

但槽点是树状数组优化和不开树状数组优化跑起来竟然差不多

#define int ll
const int N = 1010;
int n,m,q;
 
int tr[N][N];
 
void add(int x,int y) {
    for(int i = x;i<N;i+=lowbit(i)) {
        for(int j = y;j<N;j+=lowbit(j)) {
            tr[i][j] += x * y;
        }
    }
}
 
int sum(int x,int y) {
    ll res = 0;
    for(int i = x;i;i-=lowbit(i)) {
        for(int j = y;j;j-=lowbit(j)) {
            res += tr[i][j];
        }
    }
    return res;
}
 
void solve()
{
//    cin>>n>>m;
ms(tr,0);
    cin>>n>>q;
    int ss = 0;
    fo(i,1,n) {
        int x,y;
        cin>>x>>y;
        add(x,y);
        ss += x * y;
    }
//    db(ss);
    fo(i,1,q) {
        int hs,ws,hb,wb;
        cin>>hs>>ws>>hb>>wb;
        cout<<sum(hb-1,wb-1) + sum(hs,ws) - sum(hb-1,ws) - sum(hs,wb-1)<<endl;
    }
}

F. L-shapes

 

 

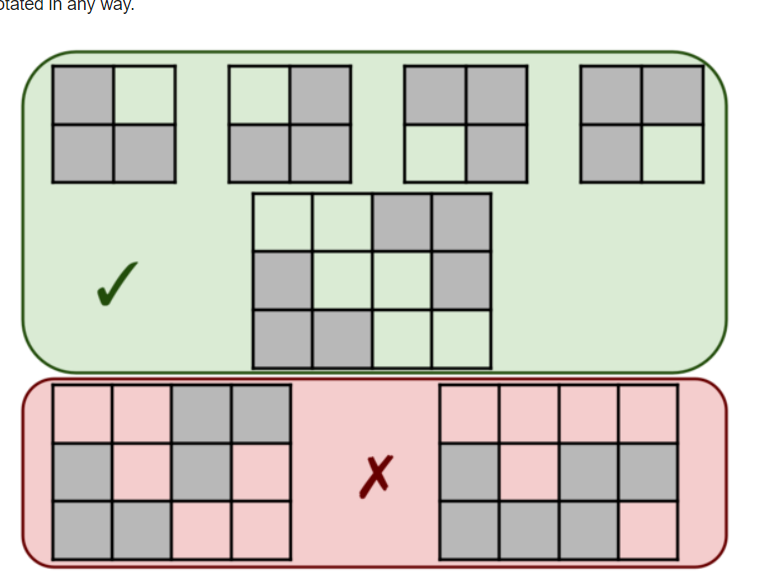
 题意是空间内只存在 L 型方块

且所有L 型的尖角不能碰到

1.遍历所有的四个四个的方块，假如有一个方块是两个且是这个形状就不能通过

 

 

 2.遍历所有点，遇到 方块上的点就bfs一遍，如果跟这个点相邻的所有点的总和不是三个，或者其中某一个点和一开始的点的曼哈顿距离是 2 （一条线），就跳出报错

//#define int ll
const int N = 60;
int n,m;
 
char mp[N][N];
 
bool check(int i,int j) {
    queue<pii> q;
    int sum = 0;    
    q.push({i,j});
    while(q.size()) {
        auto tmp = q.front();
        q.pop();int x = tmp.x,y = tmp.y;
        mp[x][y] = '.';
        sum ++ ;
        if(sum >= 4) {
            return false;
        }
        if(x == i && abs(y - j) == 2  || y == j && abs(x - i) == 2) {
            return false;
        }
        if(mp[x+1])
        fo(i,0,3) {
            int xx = x + dx[i],yy = y + dy[i];
            if(xx < 1 || yy < 1 || xx > n || yy > m) continue;
            if(mp[xx][yy] == '*')
            q.push({xx,yy}); 
        }
    }
    if(sum <= 2) return 0;
    return true;
}
 
bool check1(int x,int y) {
    int sum = (mp[x][y] == '*') + (mp[x+1][y+1] == '*') + (mp[x+1][y] == '*') + (mp[x][y+1] == '*');
    if(sum == 2) {
        if(mp[x][y] == '*') {
            if(mp[x+1][y+1] == '*') {
                return 0;
            } else return 1;
        } else {
            if(mp[x + 1][y + 1] != '*') {
                return 0;
            } else return 1;
        }
    }
    return 1;
}
 
void solve()
{
    cin>>n>>m;
    fo(i,1,n) {
        fo(j,1,m) {
            cin>>mp[i][j];
        }
    }
    //1.不能在一个矩形里连成3个
    //
    
    fo(i,1,n-1) {
        fo(j,1,m-1) {
            if(!check1(i,j)) {
                cout<<"NO"<<endl;
                rt;
            }
        }
    }
    
    fo(i,1,n) {
        fo(j,1,m) {
            if(mp[i][j] == '*') {
                if(!check(i,j)) {
                    cout<<"NO"<<endl;rt;
                }
            }
        }
    } 
    cout<<"YES"<<endl;
}

G. Even-Odd XOR

题意：n 个不同的数，奇数位异或和 与 偶数位异或和要相等。

分析

四个四个考虑

x1 ^ x3 == x2 ^ x4 == 1

也就是一奇一偶，能保证异或和相等

但如果 n % 4 == 1

就在最后一个位置加上一个 0

如果 n % 4 == 3

就在一开始的6个位置三个三个考虑，使它们异或和相等

4 1 2 12 3 8 即可

 

int ans[N];
void solve()
{
//    cin>>n>>m;
    cin>>n;
    if(n == 3) {
        cout<<2<<' '<<1<<' '<<3<<endl;
        rt;
    }
    int t = n / 2;
    if(t % 2 == 0) {
        int even1 = (1ll << 31) - 1,even2 = (1ll<<31) - 2;
        int odd1 = 2,odd2 =3;
        for(int i = 1;i<=n;i+=4) {
            ans[i] = odd1;
            ans[i+2] = odd2;
            odd1 += 2,odd2 += 2;
        }
        for(int i = 2;i<=n;i+=4) {
            ans[i] = even1;
            ans[i+2] = even2;
            even1 -= 2;
            even2 -= 2;
        }
    } else {
        int even1 = (1ll << 31) - 1,even2 = (1ll << 31) - 2;
        int odd1 = 14,odd2 = 15;
        ans[1] = 2,ans[3] = 6,ans[5] = 5;
        ans[2] = 4,ans[4] = 8,ans[6] = 13;
        for(int i = 7;i<=n;i+=4) {
            ans[i] = odd1;
            ans[i+2] = odd2;
            odd1 += 2,odd2 += 2;
        } 
        for(int i = 8;i<=n;i+=4) {
            ans[i] = even1;
            ans[i+2] = even2;
            even1 -= 2;
            even2 -= 2;
        }
    }
    if(n & 1) ans[n] = 0;
    fo(i,1,n) cout<<ans[i]<<' ';cout<<endl;
}