3302. 表达式求值

3302. 表达式求值

题目： 3302. 表达式求值 - AcWing题库

“表达式求值”问题，两个核心关键点：

（1）双栈，一个操作数栈，一个运算符栈；

（2）运算符优先级，栈顶运算符，和，即将入栈的运算符的优先级比较：
如果栈顶的运算符优先级低，新运算符直接入栈

以1+2+3x4x5举例，看是如何利用上述两个关键点实施计算的。

首先，这个例子只有+和*两个运算符，所以它的运算符表是：

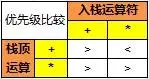
这里的含义是：

（1）如果栈顶是+，即将入栈的是+，栈顶优先级高，需要先计算，再入栈；

（2）如果栈顶是+，即将入栈的是*，栈顶优先级低，直接入栈；

（3）如果栈顶是*，即将入栈的是+，栈顶优先级高，需要先计算，再入栈；

（4）如果栈顶是*，即将入栈的是*，栈顶优先级高，需要先计算，再入栈；

有运算符后，再进行字符串的读入

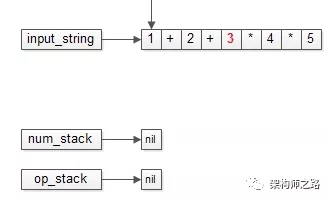
一开始，初始化好输入的字符串，以及操作数栈，运算符栈。

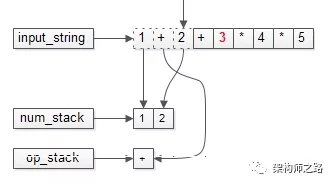
一步步，扫描字符串，操作数一个个入栈，运算符也入栈。

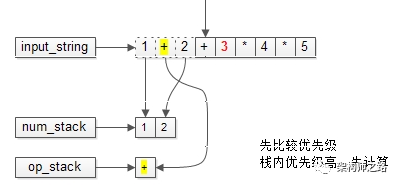
下一个操作符要入栈时，需要先比较优先级。

栈内的优先级高，必须先计算，才能入栈。

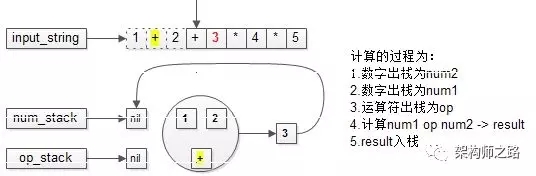
计算的过程为：

（1）操作数出栈，作为num2；

（2）操作数出栈，作为num1；

（3）运算符出栈，作为op；

（4）计算出结果；

接下来，运算符和操作数才能继续入栈。下一个操作符要入栈时，继续比较与栈顶的优先级。

栈内的优先级低，可以直接入栈。

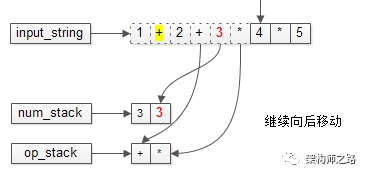
字符串继续移动。

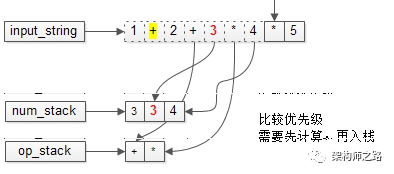
又要比较优先级了。

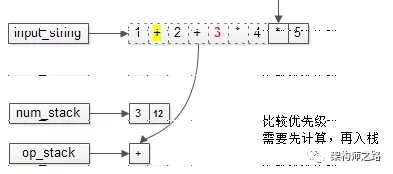
栈内的优先级高，还是先计算（3*4=12），再入栈。

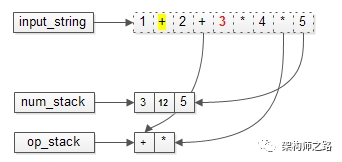
不断入栈，直到字符串扫描完毕。

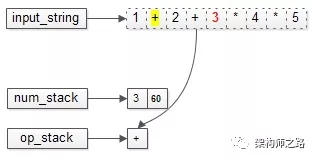
不断出栈，直到得到最终结果3+60=63，算法完成。

如果栈顶的运算符优先级高，先出栈计算，新运算符再入栈

这个方法的时间复杂度为O(n)，整个字符串只需要扫描一遍。

运算符有+-*/()~^&都没问题，如果共有n个运算符，会有一个n*n的优先级表。

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;
stack<int> num;
stack<char> op;
//优先级表 注意这里是undered_map
unordered_map<char, int> h{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}};

//比较优先级后，如果需要弹出两个数字和操作符 则计算需要弹出的两个数字
void eval()
{
    int a = num.top(); //第二个操作数
    num.pop();
    
    int b = num.top(); //第一个操作数
    num.pop();
    
    char p = op.top(); //运算符
    op.pop();
    int ans = 0;
    if(p == '+')  ans = b + a;
    if(p == '-')  ans = b - a;
    if(p == '*')  ans = b * a;
    if(p == '/')  ans = b / a;
    
    num.push(ans); //结果入栈
 }


int main()
{
    string s;  //读入表达式
    cin >> s;
    
    
    for(int i = 0; i < s.size(); i++)
    {
        if(isdigit(s[i])) //数字入栈
        {
            int x = 0, j = i;  //计算数字
            
            while(j < s.size() && isdigit(s[j]))
            {
                x = x * 10 + s[j] - '0';
                j++;
            }
            num.push(x);
            i = j - 1;  //j 多加了一次  注意这里是i = j - 1
        }
        else if(s[i] == '(')  //左括号无优先级 直接入栈
        {
            op.push(s[i]);
        }
        else if(s[i] == ')')  //右括号  需要匹配到左括号
        {
            while(op.top() != '(')  //一直计算到左括号
                eval();
            op.pop();
        }
        else
        {
            //带入栈运算符优先级低  则优先计算栈内的
            while(op.size() && h[op.top()] >= h[s[i]])
                eval();
           	op.push(s[i]); //操作符入栈
        }
    }
    
    while(op.size())  //剩余的入栈
        eval();
   
    cout << num.top() << endl; //输出结果
    return 0;
}