题解 P1632 点的移动
P1632 点的移动
题目描述
平面上有N个整数坐标点。如果将点（x0,y0）移动到（x1,y1），则需要的代价为|x0-x1|+|y0-y1|。求使得K(K=1,…,N)个点在同一位置上最少需要的代价。
输入输出格式
输入格式：
第一行一个正整数N；
接下来N行，每行两个正整数xi和yi，为第i个点的坐标，不超过10^6。
输出格式：
输出共N行，第i行为使得有i个点在统一位置的最少代价。
输入输出样例
输入样例#1：
4
15 14
15 16
14 15
16 15
输出样例#1：
0
2
3
4
【数据规模】
对于100%的数据中，满足1<=N<=50。
思路：
先说一下我犯得一个严重错误。题目没读清。让输出移动k个点的，而不是n个。一定要
认真读题
啊。
这个题是暴力枚举，可是，为什么可以。
下面让我们想一下这个；
则需要的代价为|x0-x1|+|y0-y1|。求使得K(K=1,…,N)个点在同一位置上最少需要的代价。
最优的点的横纵坐标一定来源于已知点的横纵坐标
为什么这么说呢，联想两点之间线段最短，如果有两个点，把它们移动到一个点上，最优解是移动到他两个连线的线段上。
比方说下面的图
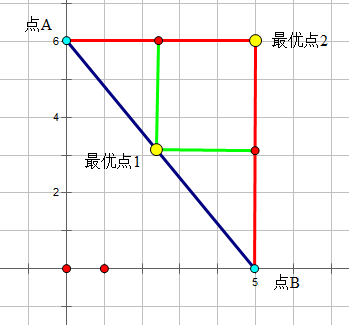
1是一个最优点，而根据曼哈顿距离的计算公式，我们可以发现，最优点2与最优点1是等效的。
我们考虑找到每两个点的最优点，这些点的最优点又会在最优点连城的线段上。
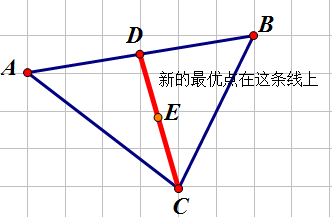
而这个点，又可以经过转化，转到一个横纵坐标已知的点上。
而且就算是多边形也没有关系啊。
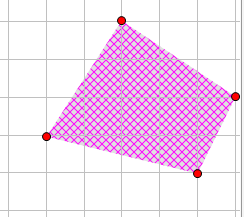
最优点一定在网格区域内，网格区域的点又可以转化位已知的点的横纵坐标。
现在就证明了枚举横纵坐标的 正确性 了
下面还有有一个要注意的点。本人的最大值付为了0x7fffff；
然后
看看这个QAQ
\({\Huge\color{Salmon}{Make-sure-your-maximum-is-the-maximum}}\)
付成0x7fffffff就可以了。
\({\color{Green}{By}}\)
\({\color{Green}{enceladus}}\)
最后献上本人丑陋的代码,(代码有锅，勿抄，不要变棕啊）
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define INF 0x7fffffff
#define ll long long
#define IL inline
#define R register
using namespace std;
ll ans[57];
int x[57],y[57];
long long l[57];
ll tot=0;
int mx,my;
int n;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>x[i]>>y[i];
ans[i]=0x7fffffff;
}
for(int j=1;j<=n;j++)
{
for(int k=1;k<=n;k++)
{
for(int t=1;t<=n;t++)
{
l[t]=abs(x[t]-x[j])+abs(y[t]-y[k]);
}
tot=0;
sort(l+1,l+1+n);
for(int i=1;i<=n;i++)
{
tot+=l[i];
ans[i]=min(ans[i],tot);
}
}
}
for(int i=1;i<=n;i++)
{
cout<<ans[i]<<endl;
}
return 0;
}
