Codeforces Round #791(Div 2)——D

D

Problem - D - Codeforces

题意：

　　给定一个有向图，每个点有自己的点权，求一条长度为K的路径使得路径上的最大点权最小，输出该条路径上的最大点权。

思路：(二分+拓扑排序)

　　最小值最大的题考虑二分解决。

　　我们每次二分答案为mx，以此判断有没有某条路径的最大值为mx且长度为k。因为我们要保证二分出来的mx是该条路径上最大的点权，所以所有大于mx的点我们都要舍弃。

　　其次如果路径中含环那必然是可以的，如果不含吗，就需要判断是否存在长度为k，最大值为mx的路径

　　举个例子：

　　　　最初的图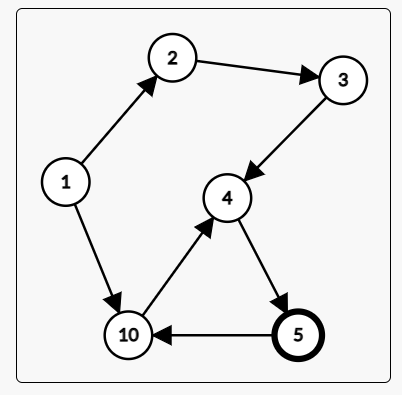　　　　　　　

　　当k == 4时，当我们判断mid = 4(既mx=4)时，则存在这样一条路径

　   　　　　　　　　　　　　　

 

　　　　chick返回true

　　判断环的时候可以通过拓扑排序来判断

　　在chick的时候需要注意的是，因为我们每次取的是小于等于mx的点，所以每次每个点的入度都不同，都需要重新统计

const int N = 2e5 + 10,INF = 0x3f3f3f3f3f;
int n, m, k, w[N];
vector<int> g[N];
int vis[N], deg[N], deep[N];/*vis判断是否小于等于mx，deg统计入度，deep统计路径长度*/
vector<pair<int, int> >e;

bool chick(int mx) {
    for (int i = 1; i <= n; ++i) vis[i] = 0, deg[i] = 0, deep[i] = -INF;
    for (int i = 1; i <= n; ++i) {
        if (w[i] <= mx)vis[i] = 1;
    }
    for (auto it : e) {
        if (w[it.first] <= mx && w[it.second] <= mx) {
            deg[it.second]++;
        }
    }
    queue<int> q;
    for (int i = 1; i <= n; ++i ) {
        if (vis[i] && !deg[i])q.push(i),deep[i] = 1;
    }
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int s : g[u]) {
            if (!vis[s]) continue;
            deep[s] = max(deep[s], deep[u] + 1);
            if (deep[s] >= k) return 1;
            deg[s]--;
            if (deg[s] == 0) q.push(s);
        }
    }
    for (int i = 1; i <= n; ++i) {
        if (vis[i] && deg[i] > 0)return 1;

    }
    return 0;
}

void solve() {
    cin >> n >> m >> k;
    for (int i = 1; i <= n; ++i) cin >> w[i];
    for (int i = 1; i <= m; ++i) {
        int x, y;
        cin >> x >> y;
        g[x].push_back(y);
        e.push_back({x, y});
    }
    if (k == 1) {
        cout << *max_element(w + 1, w + 1 + n) << endl;
        return;
    }
    int ans = INF;
    int l = 0, r = 1e9 + 1;
    for (int i = 1; i <= 50; ++i) {
        int mid = (l + r) >> 1;
        if (chick(mid)) {
            ans = min(ans, mid);
            r = mid - 1;
        } else l = mid + 1;
    }
    if (ans == INF) {
        cout << -1 << endl;
    } else cout << ans << endl;
}