结对项目作业
| 这个作业属于哪个课程 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience |
|---|---|
| 这个作业要求在哪里 | https://edu.cnblogs.com/campus/gdgy/Class34Grade23ComputerScience/homework/13479 |
| 这个作业的目标 | 实现一个自动生成小学四则运算题目的命令行程序 |
项目成员:莫圣韬 戴宏翔
1.github链接
https://gitee.com/elysiak/Paired-project
2.psp表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 40 | 50 |
| Estimate | 估计这个任务需要多少时间 | 10 | 15 |
| Requirements Analysis | 需求分析 | 30 | 35 |
| Development | 开发 | 590 | 580 |
| Analysis | 需求分析(包括学习新技术) | 70 | 100 |
| Design Spec | 生成设计文档 | 40 | 35 |
| Design Review | 设计复审 | 30 | 25 |
| Coding Standard | 代码规范制定 | 20 | 15 |
| Architecture Design | 架构设计 | 60 | 70 |
| Detailed Design | 详细设计 | 40 | 45 |
| Coding | 具体编码 | 180 | 200 |
| Code Review | 代码复审 | 40 | 30 |
| Unit Test | 单元测试 | 30 | 20 |
| Integration Test | 集成测试 | 30 | 20 |
| System Test | 系统测试 | 30 | 20 |
| Reporting | 报告 | 80 | 135 |
| Test Report | 测试报告 | 40 | 45 |
| Performance Analysis | 性能分析报告 | 30 | 35 |
| Size Measurement | 计算工作量 | 10 | 15 |
| Postmortem & Process Improvement Plan | 事后总结,并提交过程改进计划 | 30 | 40 |
| Total | 合计 | 710 | 765 |
3.效能分析
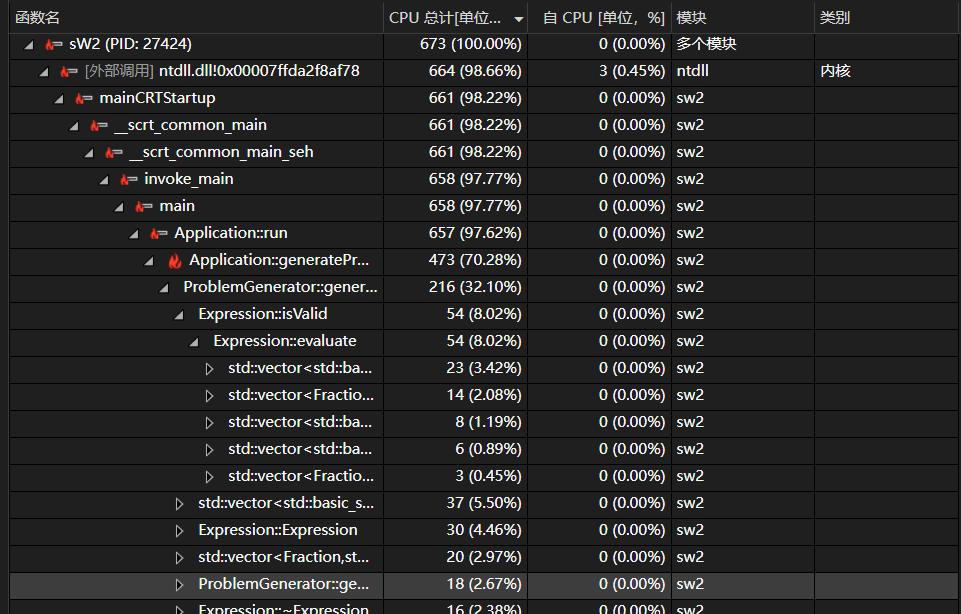
由图可以看出性能瓶颈是exression类中的evaluate函数
原来的问题:
- 在乘除法处理阶段,每次删除操作都会导致向量中元素的移动,这在表达式较长时会造成较大的性能开销。
- 循环中嵌套了删除操作,导致最坏情况下时间复杂度为O(n^2)。
优化后
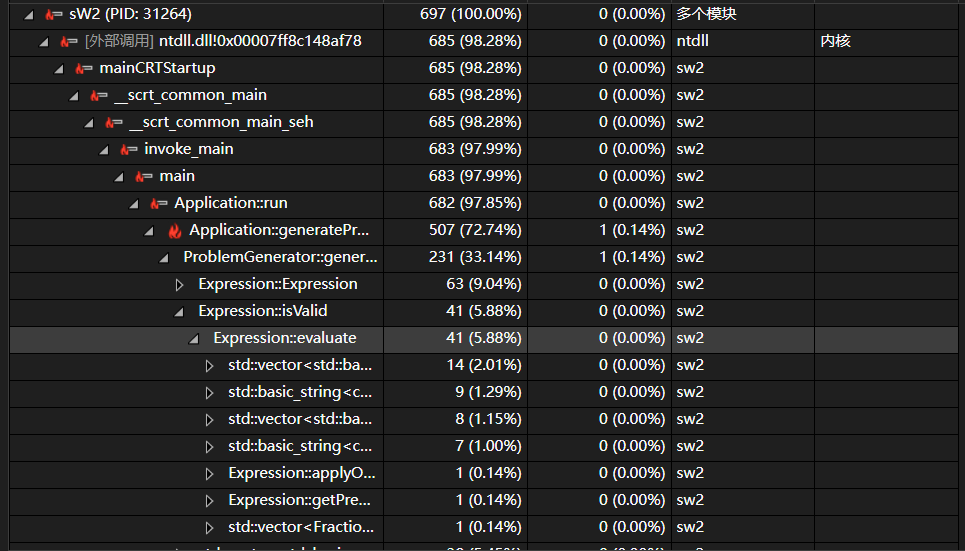
优化思路
使用两个栈:一个存储操作数(numStack),一个存储运算符(opStack)。
遍历表达式中的每个元素(操作数和运算符):
- 遇到操作数,压入操作数栈。
- 遇到运算符,与运算符栈顶的运算符比较优先级:
如果栈顶运算符优先级不低于当前运算符,则从操作数栈弹出两个操作数,从运算符栈弹出一个运算符,进行计算,并将结果压入操作数栈。重复此过程直到栈顶运算符优先级低于当前运算符或 栈为空。然后将当前运算符压入运算符栈。遍历结束后,将运算符栈中剩余的运算符依次弹出并计算,直到运算符栈为空。
操作数栈中剩下的最后一个数就是表达式的结果。
4.设计实现过程
类
类1: Fraction (分数类)
功能:表示和操作分数
方法:
- 构造函数(整数、字符串)
- 算术运算(+、-、×、÷)
- 比较运算(==、<、>、<=、>=、!=)
- 简化分数
- 字符串转换
类2: Expression (表达式类)
功能:表示和计算数学表达式
核心方法:
- evaluate():表达式求值(双栈算法)
- isValid():表达式有效性检查
- toString():表达式字符串表示
类3: ProblemGenerator (题目生成器)
职责:生成随机的有效表达式
核心方法:
- generate():生成随机表达式
- generateNumber():生成随机数
- generateOperator():生成随机运算符
类4: Application (应用程序)
功能:协调整个程序流程
核心方法:
- generateProblems():生成题目文件
- checkAnswers():检查答案
- parseExpression():解析表达式字符串
- run():主运行逻辑
关键函数
Expression::evaluate()
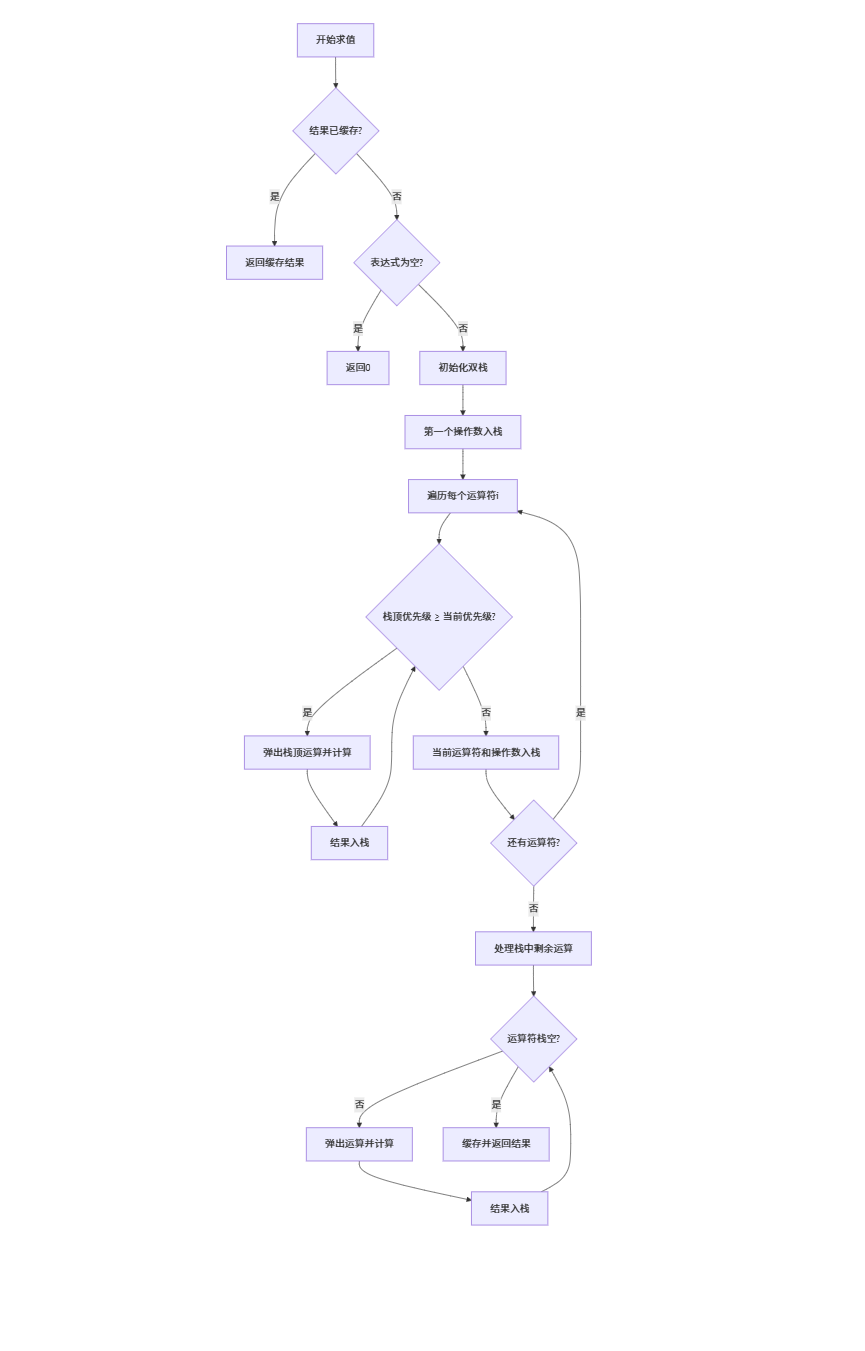
ProblemGenerator::generate()
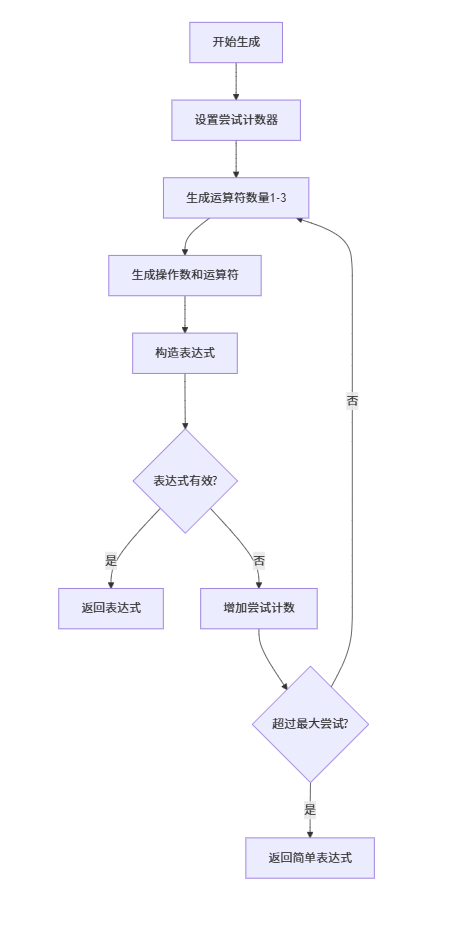
Application::generateProblems()
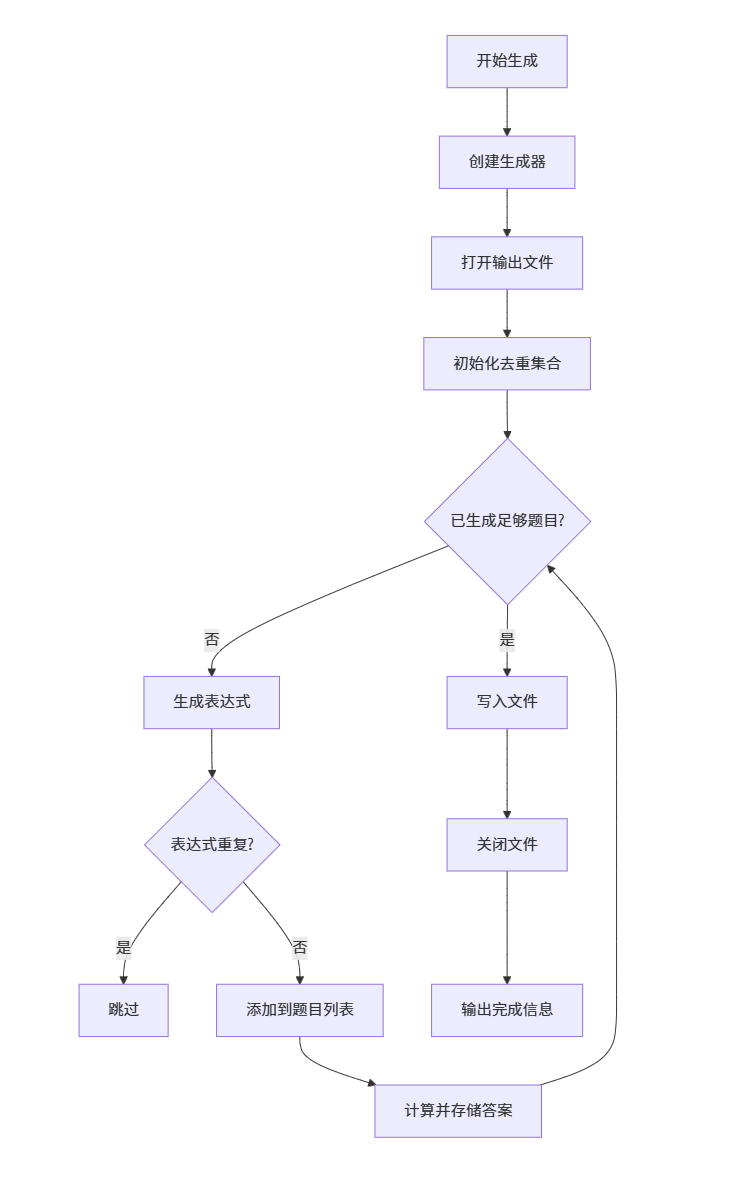
Application::checkAnswers()
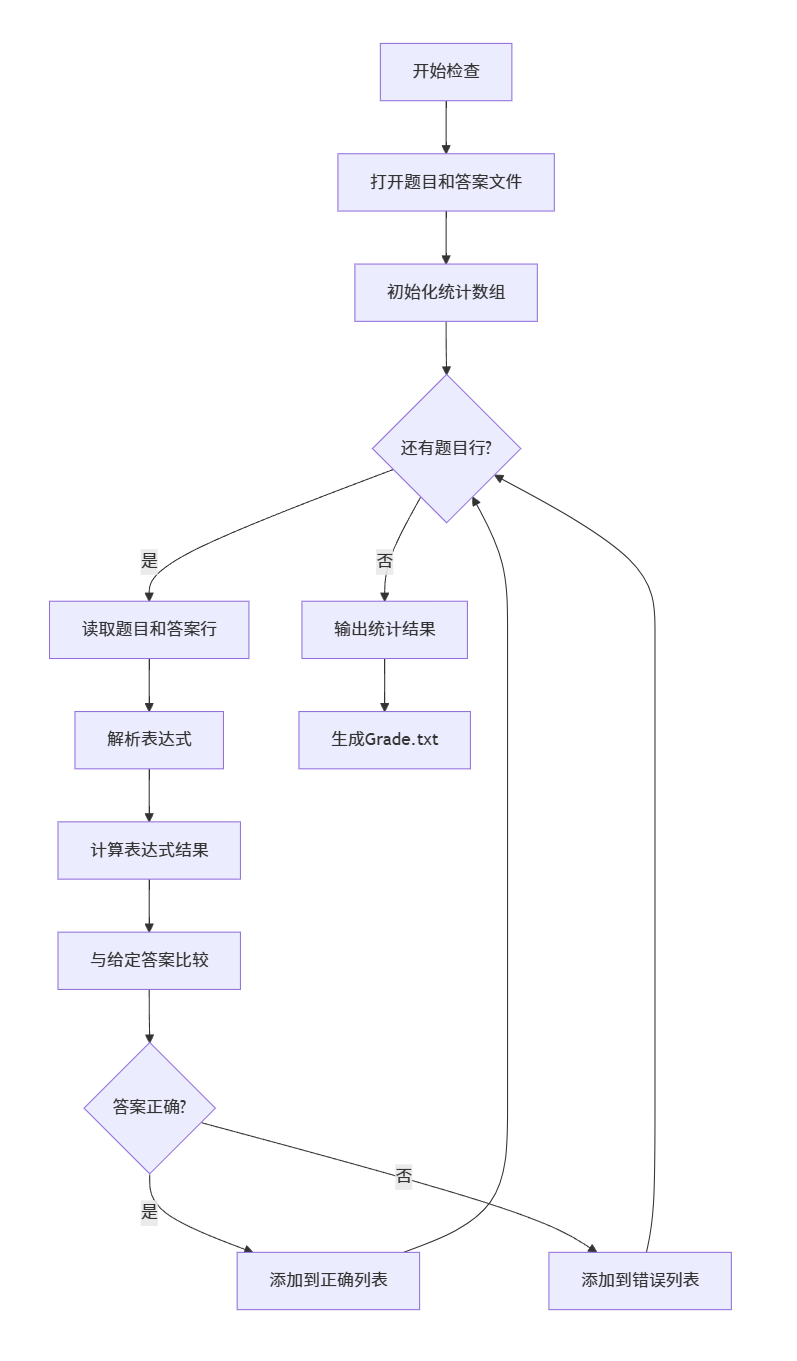
5.代码说明
Fraction
点击查看代码
class Fraction {
private:
int numerator; // 分子
int denominator; // 分母
// 分数简化函数,将分数约分到最简形式
// 通过计算分子和分母的最大公约数,将分数化为最简形式
// 如果分子为0,则将分母设为1,表示0值分数
void simplify() {
if (numerator == 0) {
denominator = 1; // 0值分数统一表示为0/1
return;
}
// 计算分子和分母的最大公约数,注意分子取绝对值
int gcd_val = gcd(std::abs(numerator), denominator);
numerator /= gcd_val; // 分子约分
denominator /= gcd_val; // 分母约分
}
// 计算两个整数的最大公约数(GCD)
// 使用欧几里得算法递归计算最大公约数
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
public:
// 构造函数,通过分子分母创建分数
// 自动处理分母为0或负数的情况,并自动简化分数
Fraction(int num = 0, int den = 1) : numerator(num), denominator(den) {
if (denominator == 0) denominator = 1; // 防止除零错误,分母设为1
if (denominator < 0) {
// 确保分母始终为正,负号转移到分子
numerator = -numerator;
denominator = -denominator;
}
simplify(); // 构造完成后自动简化分数
}
// 字符串构造函数,支持多种分数格式
// 自动识别并解析带分数、真分数和整数格式
Fraction(const std::string& str) {
if (str.find('\'') != std::string::npos) {
// 处理带分数格式:a'b/c (如 "2'1/2" 表示 2又1/2)
size_t pos1 = str.find('\''); // 定位单引号位置
size_t pos2 = str.find('/'); // 定位斜杠位置
int integer = std::stoi(str.substr(0, pos1)); // 提取整数部分
int num = std::stoi(str.substr(pos1 + 1, pos2 - pos1 - 1)); // 提取分子
int den = std::stoi(str.substr(pos2 + 1)); // 提取分母
// 将带分数转换为假分数:a'b/c = (a×c + b)/c
numerator = integer * den + (integer >= 0 ? num : -num);
denominator = den;
}
else if (str.find('/') != std::string::npos) {
// 处理真分数格式:a/b (如 "3/4")
size_t pos = str.find('/');
numerator = std::stoi(str.substr(0, pos)); // 提取分子
denominator = std::stoi(str.substr(pos + 1)); // 提取分母
}
else {
// 处理整数格式 (如 "5")
numerator = std::stoi(str);
denominator = 1; // 整数分母为1
}
simplify(); // 解析完成后自动简化
}
// 将分数转换为字符串表示
// 根据分数的值自动选择最合适的显示格式
std::string toString() const {
if (numerator == 0) {
return "0"; // 0值分数直接返回"0"
}
if (denominator == 1) {
return std::to_string(numerator); // 整数直接返回数字字符串
}
int integer = numerator / denominator; // 整数部分
int remainder = std::abs(numerator) % denominator; // 余数部分(取绝对值)
if (integer == 0) {
// 真分数格式:分子/分母 (如 "3/4")
return std::to_string(numerator) + "/" + std::to_string(denominator);
}
else if (remainder == 0) {
// 整数格式 (如 "2")
return std::to_string(integer);
}
else {
// 带分数格式:整数'分子/分母 (如 "2'1/2")
return std::to_string(integer) + "'" + std::to_string(remainder) + "/" + std::to_string(denominator);
}
}
// 分数加法运算符重载
// 通过通分后分子相加实现分数加法
Fraction operator+(const Fraction& other) const {
int num = numerator * other.denominator + other.numerator * denominator;
int den = denominator * other.denominator;
return Fraction(num, den); // 返回新分数,会自动简化
}
// 分数减法运算符重载
// 通过通分后分子相减实现分数减法
Fraction operator-(const Fraction& other) const {
int num = numerator * other.denominator - other.numerator * denominator;
int den = denominator * other.denominator;
return Fraction(num, den);
}
// 分数乘法运算符重载
// 分子乘分子,分母乘分母实现分数乘法
Fraction operator*(const Fraction& other) const {
int num = numerator * other.numerator;
int den = denominator * other.denominator;
return Fraction(num, den);
}
// 分数除法运算符重载
// 通过乘以倒数实现分数除法,有除零保护
Fraction operator/(const Fraction& other) const {
if (other.numerator == 0) {
return Fraction(0, 1); // 除零保护,返回0
}
// 分数除法:a/b ÷ c/d = a/b × d/c
int num = numerator * other.denominator;
int den = denominator * other.numerator;
return Fraction(num, den);
}
// 分数相等比较运算符
// 比较化简后的分子和分母是否完全相同
bool operator==(const Fraction& other) const {
return numerator == other.numerator && denominator == other.denominator;
}
// 分数小于比较运算符
// 通过交叉相乘比较分数大小,避免浮点数精度问题
bool operator<(const Fraction& other) const {
return numerator * other.denominator < other.numerator * denominator;
}
// 分数大于比较运算符
// 基于小于运算符实现:a > b 等价于 b < a
bool operator>(const Fraction& other) const {
return other < *this;
}
// 分数小于等于比较运算符
// 基于小于运算符实现:a <= b 等价于 !(b < a)
bool operator<=(const Fraction& other) const {
return !(other < *this);
}
// 分数大于等于比较运算符
// 基于小于运算符实现:a >= b 等价于 !(a < b)
bool operator>=(const Fraction& other) const {
return !(*this < other);
}
// 分数不等于比较运算符
// 基于等于运算符实现:a != b 等价于 !(a == b)
bool operator!=(const Fraction& other) const {
return !(*this == other);
}
// 检查分数是否为真分数
// 真分数定义:|分子| < 分母
bool isProper() const {
return std::abs(numerator) < denominator;
}
// 检查分数是否为非负数
// 仅检查分子,因为分母始终为正
bool isNonNegative() const {
return numerator >= 0;
}
// 检查分数是否为零
// 检查分子是否为0
bool isZero() const {
return numerator == 0;
}
};
Expression
点击查看代码
class Expression {
private:
std::vector<Fraction> numbers; // 存储表达式中的所有操作数
std::vector<std::string> operators; // 存储表达式中的所有运算符
// 缓存机制:存储已计算的结果,避免重复计算
mutable Fraction cachedResult; // 缓存的计算结果
mutable bool isResultCached; // 标记结果是否已缓存
// 预分配的栈空间:用于双栈算法,避免重复内存分配
mutable std::vector<Fraction> numStack; // 操作数栈
mutable std::vector<std::string> opStack; // 运算符栈
// 获取运算符的优先级
// 返回运算符的优先级数值,数值越大优先级越高
int getPrecedence(const std::string& op) const {
if (op == "*" || op == "/") return 2; // 乘除法优先级最高
if (op == "+" || op == "-") return 1; // 加减法优先级较低
return 0; // 其他运算符默认优先级
}
// 应用具体的运算操作
// 根据运算符类型执行相应的分数运算
Fraction applyOperation(const Fraction& left, const Fraction& right, const std::string& op) const {
if (op == "+") return left + right; // 加法运算
if (op == "-") return left - right; // 减法运算
if (op == "*") return left * right; // 乘法运算
if (op == "/") {
if (right.isZero()) return Fraction(0, 1); // 除零保护,返回0
return left / right; // 除法运算
}
return Fraction(0, 1); // 未知运算符返回0
}
// 表达式求值函数,使用双栈算法
// 实现运算符优先级处理,确保乘除法先于加减法执行
Fraction evaluate() const {
// 如果已经计算过结果,直接返回缓存的值,避免重复计算
if (isResultCached) {
return cachedResult;
}
// 处理空表达式的情况
if (numbers.empty()) {
cachedResult = Fraction(0, 1);
isResultCached = true;
return cachedResult;
}
// 清空栈空间但保留预分配的容量,避免重复内存分配
numStack.clear();
opStack.clear();
// 第一个操作数直接压入操作数栈
numStack.push_back(numbers[0]);
// 遍历所有运算符和对应的操作数
for (size_t i = 0; i < operators.size(); i++) {
const std::string& currentOp = operators[i]; // 当前运算符
const Fraction& currentNum = numbers[i + 1]; // 当前操作数
// 处理运算符优先级:当栈顶运算符优先级不低于当前运算符时,先计算栈顶运算
// 这确保了乘除法在加减法之前执行
while (!opStack.empty() &&
getPrecedence(opStack.back()) >= getPrecedence(currentOp)) {
// 从栈中弹出运算符和操作数进行计算
Fraction right = numStack.back(); numStack.pop_back();
Fraction left = numStack.back(); numStack.pop_back();
std::string op = opStack.back(); opStack.pop_back();
// 执行运算并将结果压回操作数栈
Fraction result = applyOperation(left, right, op);
numStack.push_back(result);
}
// 当前运算符和操作数入栈,等待后续处理
opStack.push_back(currentOp);
numStack.push_back(currentNum);
}
// 处理栈中剩余的运算(从左到右顺序)
while (!opStack.empty()) {
Fraction right = numStack.back(); numStack.pop_back();
Fraction left = numStack.back(); numStack.pop_back();
std::string op = opStack.back(); opStack.pop_back();
Fraction result = applyOperation(left, right, op);
numStack.push_back(result);
}
// 栈顶元素即为最终计算结果,存入缓存
cachedResult = numStack.back();
isResultCached = true;
return cachedResult;
}
// 获取运算符的显示形式
// 将内部运算符转换为用户友好的显示形式
std::string getDisplayOperator(const std::string& op) const {
if (op == "*") return "×"; // 乘法显示为×
if (op == "/") return "÷"; // 除法显示为÷
return op; // 加减法保持原样
}
public:
// 构造函数:使用操作数和运算符列表初始化表达式
// 同时预分配栈空间以提高性能
Expression(const std::vector<Fraction>& nums, const std::vector<std::string>& ops)
: numbers(nums), operators(ops), isResultCached(false) {
// 预分配足够的栈空间,避免计算过程中的重复内存分配
numStack.reserve(numbers.size()); // 操作数栈预留空间
opStack.reserve(operators.size()); // 运算符栈预留空间
}
// 将表达式转换为字符串形式,用于显示和输出
// 格式:操作数1 运算符1 操作数2 运算符2 ... 操作数n =
std::string toString() const {
std::stringstream ss;
for (size_t i = 0; i < numbers.size(); i++) {
if (i > 0) {
// 在运算符前后添加空格,提高可读性
ss << " " << getDisplayOperator(operators[i - 1]) << " ";
}
ss << numbers[i].toString(); // 添加操作数的字符串表示
}
ss << " = "; // 表达式以等号结束
return ss.str();
}
// 获取表达式的计算结果
// 如果结果已缓存则直接返回,否则调用evaluate()计算
Fraction getResult() const {
return evaluate();
}
// 检查表达式是否满足所有约束条件
// 包括数值范围、非负结果和真分数除法等要求
bool isValid(int range) const {
// 检查所有操作数是否在指定范围内 [0, range)
for (const auto& num : numbers) {
if (num < Fraction(0) || num >= Fraction(range)) {
return false; // 数值超出范围
}
}
// 检查中间计算结果是否非负
// 使用try-catch防止计算过程中出现异常
try {
Fraction result = evaluate();
if (!result.isNonNegative()) return false; // 结果为负数
}
catch (...) {
return false; // 计算过程中出现异常
}
// 检查所有除法运算的结果是否为真分数
for (size_t i = 0; i < operators.size(); i++) {
if (operators[i] == "/") {
// 确保有足够的操作数
if (i + 1 >= numbers.size()) return false;
Fraction left = numbers[i]; // 被除数
Fraction right = numbers[i + 1]; // 除数
if (right.isZero()) return false; // 除数为零
Fraction div_result = left / right;
if (!div_result.isProper()) return false; // 除法结果不是真分数
}
}
return true; // 所有检查都通过
}
// 获取表达式的规范化形式,用于去重比较
// 格式:操作数1运算符1操作数2运算符2...操作数n(无空格)
std::string getNormalizedForm() const {
std::stringstream ss;
for (size_t i = 0; i < numbers.size(); i++) {
if (i > 0) {
ss << operators[i - 1]; // 添加运算符(无空格)
}
ss << numbers[i].toString(); // 添加操作数
}
return ss.str();
}
// 访问器方法:获取操作数列表,主要用于测试
const std::vector<Fraction>& getNumbers() const { return numbers; }
// 访问器方法:获取运算符列表,主要用于测试
const std::vector<std::string>& getOperators() const { return operators; }
// 清除缓存:当表达式被修改时需要调用此方法
void clearCache() {
isResultCached = false; // 重置缓存标记
}
};
ProblemGenerator
点击查看代码
class ProblemGenerator {
private:
int range; // 数值范围,控制生成的数字大小
std::mt19937 gen; // 随机数生成器,用于产生各种随机值
// 生成随机数,支持生成整数和分数两种类型
// 根据概率控制决定生成整数还是分数,确保数值在指定范围内
Fraction generateNumber() {
std::uniform_int_distribution<> dis(1, std::max(1, range - 1));
// 概率控制:70%概率生成整数,30%概率生成真分数
// 只有在范围大于等于2时才可能生成分数
if (range >= 2 && std::uniform_real_distribution<>(0, 1)(gen) < 0.3) {
// 生成真分数:分母在[2, range]范围内,分子在[1, 分母-1]范围内
int den = std::uniform_int_distribution<>(2, range)(gen); // 随机分母
int num = std::uniform_int_distribution<>(1, den - 1)(gen); // 随机分子,确保是真分数
return Fraction(num, den);
}
else {
// 生成整数:数值在[0, range-1]范围内
return Fraction(std::uniform_int_distribution<>(0, range - 1)(gen), 1);
}
}
// 生成随机运算符
// 从四种基本运算符中随机选择一种
std::string generateOperator() {
static std::vector<std::string> ops = { "+", "-", "*", "/" }; // 可用的运算符集合
std::uniform_int_distribution<> dis(0, ops.size() - 1); // 随机索引生成器
return ops[dis(gen)]; // 返回随机选择的运算符
}
public:
// 构造函数:初始化数值范围和随机数生成器
// 使用真随机数种子确保每次运行生成不同的题目
ProblemGenerator(int r) : range(r) {
std::random_device rd; // 真随机数设备,用于生成种子
gen.seed(rd()); // 用真随机数初始化伪随机数生成器
}
// 生成有效的数学表达式
// 通过多次尝试确保生成的表达式满足所有约束条件
Expression generate() {
int attempts = 0; // 尝试计数器
const int maxAttempts = 1000; // 最大尝试次数,防止无限循环
// 尝试生成有效表达式,直到成功或达到最大尝试次数
while (attempts < maxAttempts) {
// 随机决定运算符数量(1-3个),对应2-4个操作数
int opCount = std::uniform_int_distribution<>(1, 3)(gen);
std::vector<Fraction> numbers; // 操作数容器
std::vector<std::string> operators; // 运算符容器
// 构建表达式结构:生成操作数和运算符
for (int i = 0; i <= opCount; i++) {
numbers.push_back(generateNumber()); // 生成操作数
if (i < opCount) {
operators.push_back(generateOperator()); // 生成运算符
}
}
// 创建表达式对象并验证其有效性
Expression expr(numbers, operators);
if (expr.isValid(range)) {
return expr; // 返回有效的表达式
}
attempts++; // 增加尝试计数
}
// 保底机制:如果多次尝试都失败,返回一个简单的有效表达式
// 确保函数始终有返回值,避免生成失败
return Expression({ Fraction(1), Fraction(1) }, { "+" });
}
};
Application
点击查看代码
class Application {
private:
// 生成指定数量的四则运算题目并保存到文件
// 同时生成对应的答案文件,确保题目不重复且符合所有约束条件
void generateProblems(int count, int range) {
ProblemGenerator generator(range); // 创建题目生成器,指定数值范围
std::set<std::string> generatedExpressions; // 用于存储已生成表达式的规范化形式,实现去重
std::vector<Expression> problems; // 存储有效的题目表达式
std::vector<Fraction> answers; // 存储对应的答案
// 打开输出文件,用于保存题目和答案
std::ofstream exerciseFile("Exercises.txt");
std::ofstream answerFile("Answers.txt");
// 检查文件是否成功打开
if (!exerciseFile.is_open() || !answerFile.is_open()) {
std::cerr << "无法打开输出文件!" << std::endl;
return;
}
int generated = 0; // 已生成的题目数量
const int maxAttempts = count * 10; // 最大尝试次数,防止无限循环
int attempts = 0; // 当前尝试次数
// 循环生成题目,直到达到指定数量或超过最大尝试次数
while (generated < count && attempts < maxAttempts) {
Expression problem = generator.generate(); // 生成一个题目表达式
std::string normalized = problem.getNormalizedForm(); // 获取规范化形式用于去重
// 检查表达式是否重复,基于规范化形式进行比较
if (generatedExpressions.find(normalized) == generatedExpressions.end()) {
generatedExpressions.insert(normalized); // 添加到已生成集合
problems.push_back(problem); // 添加到题目列表
answers.push_back(problem.getResult()); // 计算并存储答案
generated++; // 增加已生成计数
}
attempts++; // 增加尝试计数
}
// 将题目和答案写入文件
for (size_t i = 0; i < problems.size(); i++) {
// 写入题目文件:序号. 表达式 =
exerciseFile << (i + 1) << ". " << problems[i].toString() << std::endl;
// 写入答案文件:序号. 答案
answerFile << (i + 1) << ". " << answers[i].toString() << std::endl;
}
// 关闭文件流
exerciseFile.close();
answerFile.close();
// 输出生成结果信息
std::cout << "已生成 " << problems.size() << " 道题目到 Exercises.txt 和 Answers.txt" << std::endl;
}
// 检查答案文件的正确性,对比题目文件和答案文件
// 生成统计报告,显示正确和错误的题目编号
void checkAnswers(const std::string& exerciseFile, const std::string& answerFile) {
// 打开题目文件和答案文件
std::ifstream exFile(exerciseFile);
std::ifstream ansFile(answerFile);
// 检查文件是否成功打开
if (!exFile.is_open() || !ansFile.is_open()) {
std::cerr << "无法打开输入文件!" << std::endl;
return;
}
std::vector<int> correct, wrong; // 存储正确和错误题目的编号
std::string exLine, ansLine; // 用于读取文件的每一行
int lineNum = 1; // 当前处理的题目编号
// 逐行读取题目文件和答案文件
while (std::getline(exFile, exLine) && std::getline(ansFile, ansLine)) {
// 提取表达式和答案字符串,跳过序号部分
size_t exPos = exLine.find(". ");
size_t ansPos = ansLine.find(". ");
// 确保找到了序号分隔符
if (exPos != std::string::npos && ansPos != std::string::npos) {
std::string expressionStr = exLine.substr(exPos + 2); // 提取表达式部分
std::string givenAnswer = ansLine.substr(ansPos + 2); // 提取答案部分
// 移除表达式末尾的 "= ",还原为纯表达式
if (expressionStr.find(" = ") != std::string::npos) {
expressionStr = expressionStr.substr(0, expressionStr.length() - 3);
}
try {
// 解析表达式字符串为Expression对象
Expression expr = parseExpression(expressionStr);
// 计算表达式的正确结果
Fraction computedAnswer = expr.getResult();
// 将答案文件中的字符串转换为Fraction对象
Fraction givenAnswerFrac(givenAnswer);
// 比较计算结果与给定答案
if (computedAnswer == givenAnswerFrac) {
correct.push_back(lineNum); // 答案正确,记录题目编号
}
else {
wrong.push_back(lineNum); // 答案错误,记录题目编号
}
}
catch (...) {
// 解析或计算过程中出现异常,视为错误答案
wrong.push_back(lineNum);
}
}
lineNum++; // 处理下一题
}
// 关闭文件流
exFile.close();
ansFile.close();
// 生成批改结果文件
std::ofstream gradeFile("Grade.txt");
// 写入正确答案统计
gradeFile << "Correct: " << correct.size() << " (";
for (size_t i = 0; i < correct.size(); i++) {
gradeFile << correct[i]; // 写入题目编号
if (i < correct.size() - 1) gradeFile << ", "; // 添加逗号分隔
}
gradeFile << ")" << std::endl;
// 写入错误答案统计
gradeFile << "Wrong: " << wrong.size() << " (";
for (size_t i = 0; i < wrong.size(); i++) {
gradeFile << wrong[i]; // 写入题目编号
if (i < wrong.size() - 1) gradeFile << ", "; // 添加逗号分隔
}
gradeFile << ")" << std::endl;
gradeFile.close(); // 关闭批改结果文件
std::cout << "统计结果已输出到 Grade.txt" << std::endl;
}
// 解析表达式字符串,将其转换为Expression对象
// 支持从文件读取的表达式格式转换为内部表示
Expression parseExpression(const std::string& expr) {
std::vector<Fraction> numbers; // 存储解析出的操作数
std::vector<std::string> operators; // 存储解析出的运算符
std::stringstream ss(expr); // 使用字符串流进行分词
std::string token; // 存储每个分词
// 逐个处理分词
while (ss >> token) {
if (token == "+" || token == "-" || token == "×" || token == "÷") {
// 处理运算符:将显示格式转换为内部格式
if (token == "×") operators.push_back("*"); // 乘法符号转换
else if (token == "÷") operators.push_back("/"); // 除法符号转换
else operators.push_back(token); // 加减法符号保持不变
}
else {
// 处理数字:使用Fraction的字符串构造函数解析各种格式
numbers.push_back(Fraction(token));
}
}
// 使用解析出的操作数和运算符创建Expression对象
return Expression(numbers, operators);
}
// 显示程序使用帮助信息
// 说明命令行参数的使用方法和示例
void showHelp() {
std::cout << "使用方法:" << std::endl;
std::cout << "生成题目: Myapp.exe -n <题目数量> -r <数值范围>" << std::endl;
std::cout << "检查答案: Myapp.exe -e <题目文件> -a <答案文件>" << std::endl;
std::cout << "示例:" << std::endl;
std::cout << " Myapp.exe -n 10 -r 10" << std::endl;
std::cout << " Myapp.exe -e Exercises.txt -a Answers.txt" << std::endl;
}
public:
// 应用程序主入口函数
// 解析命令行参数并执行相应的功能
void run(int argc, char* argv[]) {
// 如果没有提供参数,显示帮助信息
if (argc < 2) {
showHelp();
return;
}
// 解析命令行参数,存储为键值对
std::map<std::string, std::string> params;
for (int i = 1; i < argc; i += 2) {
if (i + 1 < argc) {
params[argv[i]] = argv[i + 1]; // 参数名作为键,下一个参数作为值
}
}
// 检查是否为生成题目模式
if (params.find("-n") != params.end() && params.find("-r") != params.end()) {
// 提取题目数量和数值范围参数
int count = std::stoi(params["-n"]);
int range = std::stoi(params["-r"]);
// 参数验证:必须为正整数
if (count <= 0 || range <= 0) {
std::cerr << "参数必须为正整数!" << std::endl;
return;
}
// 参数验证:题目数量不能超过限制
if (count > 10000) {
std::cerr << "题目数量不能超过10000!" << std::endl;
return;
}
// 执行题目生成功能
generateProblems(count, range);
}
// 检查是否为答案检查模式
else if (params.find("-e") != params.end() && params.find("-a") != params.end()) {
// 执行答案检查功能
checkAnswers(params["-e"], params["-a"]);
}
// 参数不匹配,显示错误信息和帮助
else {
std::cerr << "参数错误!" << std::endl;
showHelp();
}
}
};
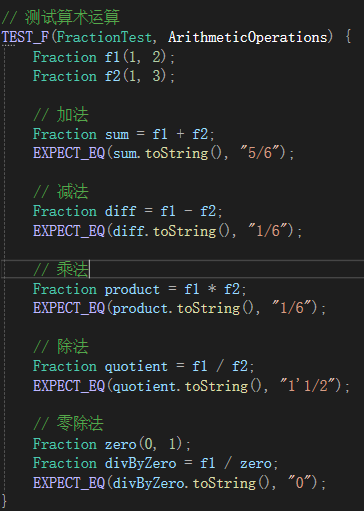
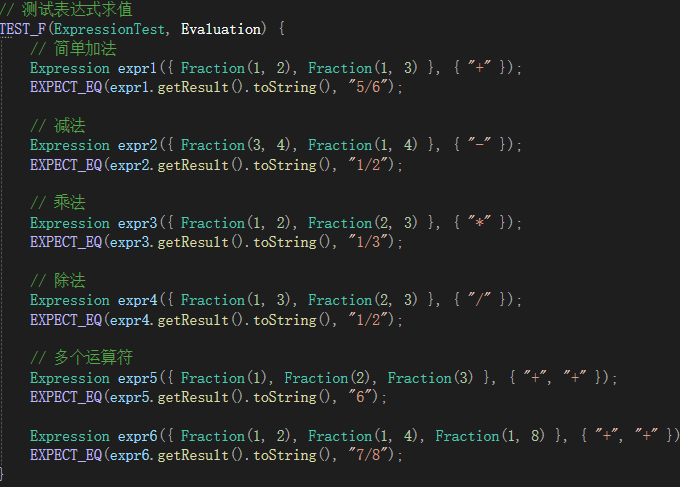
6.测试运行
测试结果
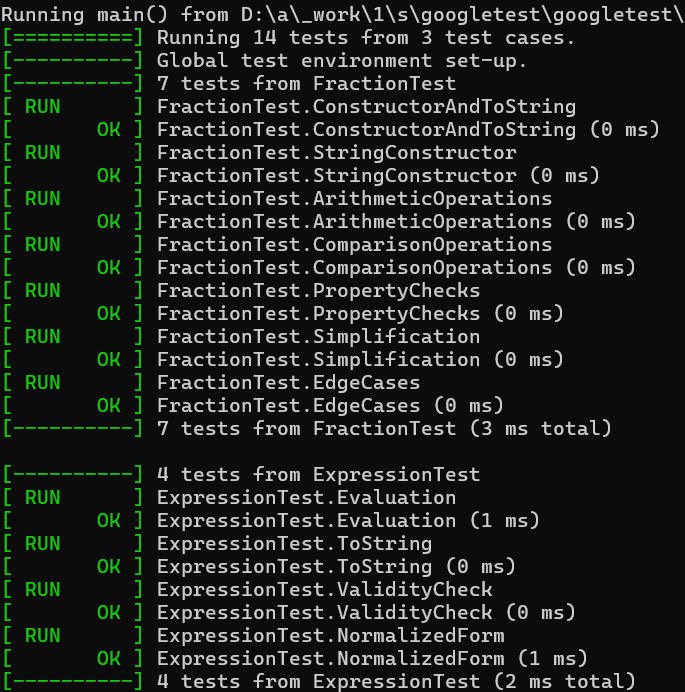
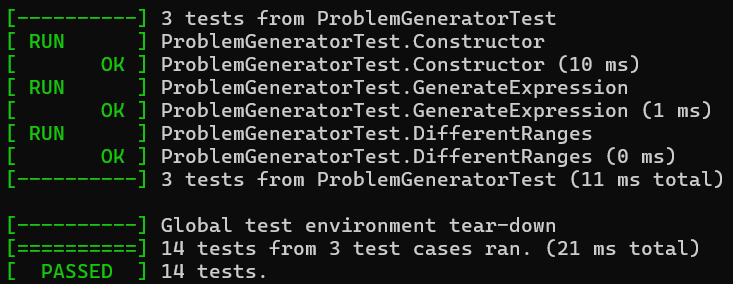
测试部分例子
exercise.txt
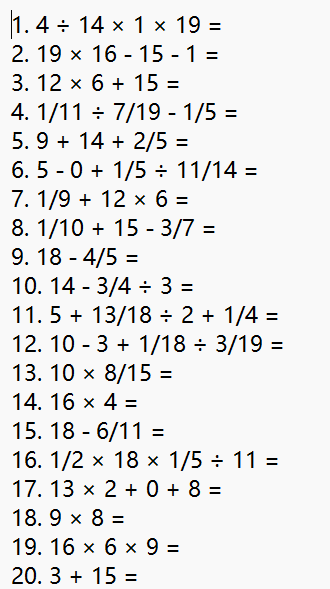
answer.txt

grade.txt
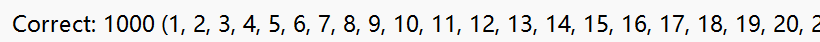
- 计算正确性验证
- 运算符优先级:确保乘除法优先于加减法
- 结果验证:每个测试用例都通过手动计算验证
- 约束条件
- 非负结果:所有表达式验证确保不产生负数
- 真分数除法:除法运算结果是真分数
- 数值范围:所有数值都在指定范围内
运算符数量:不超过3个运算符
- 边界情况处理
- 零的处理:正确处理零的运算和显示
- 负分数:负分数的运算和显示无错误
- 除零保护:防止除零出错
7.项目小结
感想
1.
这次合作开发程序,是一次非常宝贵和高效的体验。
在合作初期,我们首先对任务进行了拆分,并明确了各自负责的模块。过程中,我们不可避免地遇到了一些技术思路和实现方式上的分歧。但通过定期的代码审查和集中讨论,我们不仅高效地解决了问题,还相互借鉴了更好的编程习惯和算法思路。我的搭档莫圣韬在架构设计上很有远见,而我在细节处理和调试方面比较擅长,这种优势互补让我们的代码质量远超个人独立完成的水准。
更重要的是,这次合作让我深切体会到团队协作的力量。当遇到棘手的技术难题时,能够随时与伙伴探讨,极大地减轻了心理压力,也加速了问题的解决。最终程序的成功,是我们共同智慧和努力的结晶。
总而言之,这是一次非常成功的合作。它不仅圆满完成了开发任务,更让我在沟通协作和技术层面都获得了新的成长。
2.
在这次结对开发小学四则运算程序的过程中,我与队友深刻体会到了协作编程的魅力。我们分工明确,通过频繁的代码审查和设计讨论,确保了各模块的无缝衔接。。双栈算法的实现让我们领略了数据结构的美妙,而分数运算的完整性则考验着我们对细节的把握。面对复杂的业务约束,我们共同探讨解决方案,在争论中达成共识,在合作中相互学习。这个项目不仅提升了我们的编程能力,更培养了团队协作精神。当看到程序成功生成万道题目并准确批改时,所有的调试艰辛都化为了成就的喜悦。这次经历让我们明白,优秀的软件不仅是技术的结晶,更是团队智慧与默契的产物。
建议
代码规范与风格统一:
- 使用一致的命名规范(如变量、函数、类名的命名)。
- 统一代码格式(如缩进、括号风格等)。
- 可以使用代码格式化工具(如ClangFormat)来自动格式化代码。
模块化设计:
- 将系统划分为清晰的模块,每个模块由一个人负责。
- 定义好模块之间的接口,便于并行开发。
版本控制:
- 使用Git等版本控制工具,并制定分支管理策略(如Git Flow)。
- 定期提交代码,并编写清晰的提交信息。
代码审查:
- 互相审查代码,确保代码质量,并分享知识。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号