二叉树初步总结
二叉树的基本概念:
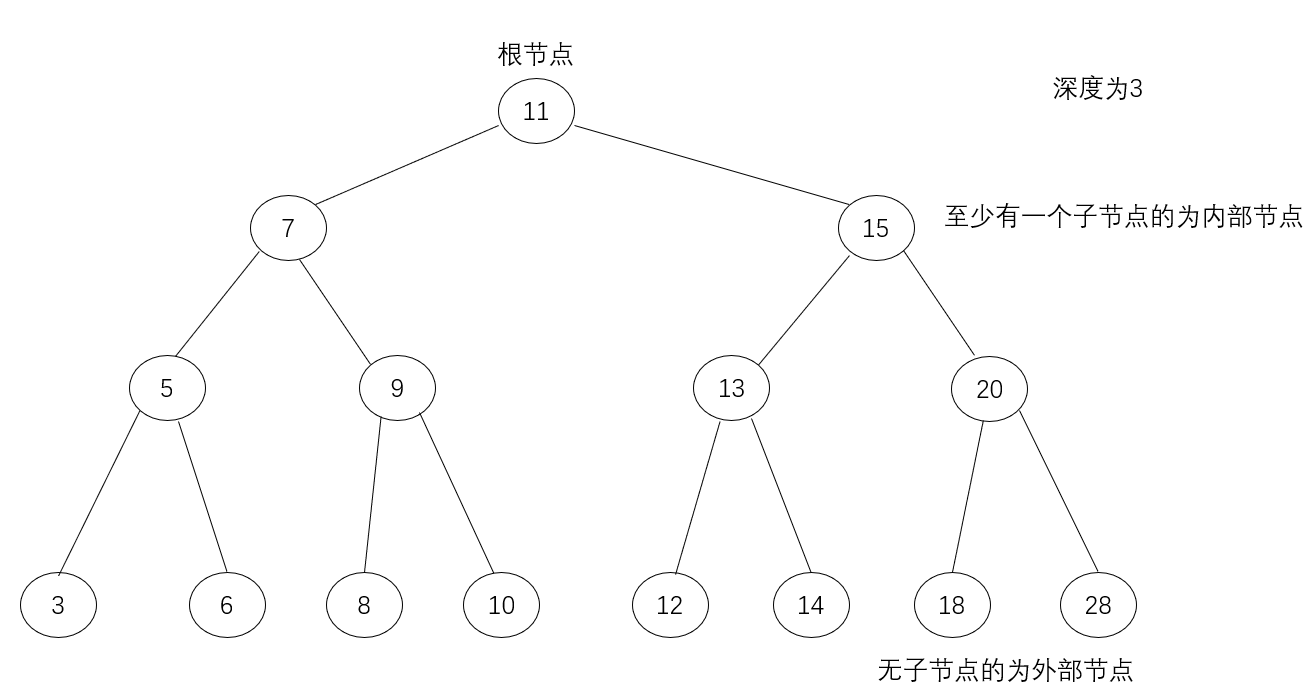
如果所示即为一个二叉树,其中基础的概念也很清晰,其余部分后续再做补充。
创建一个二叉树
二叉树的生成原理是递归,有递归一层一层是为树添加节点,代码如下:
// 1.创建二叉树,二叉树即每个节点最多只能有两个子节点,这个定义有助于高效的在树中插入、查找和删除节点的算法。
// 1. 创建二叉树
const Compare = {
LESS_THAN: -1,
BIGGER_THAN: 1,
EQUALS: 0
};
//判断两个数的大小关系,相等返回0,a>b,返回1,小于返回-1
function defaultCompare(a, b) {
if (a === b) {
return Compare.EQUALS;
}
return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
class Node {
constructor(key) {
this.key = key
this.left = null
this.right = null
}
}
class BinarySearchTree {
// constructor 用来创建和初始化对象
constructor(compareFn = defaultCompare) {
this.compareFn = compareFn
this.root = null
}
insert(key) {
if (this.root == null) {
this.root = new Node(key)
} else {
this.insertNode(this.root, key)
}
}
insertNode(node, key) {
if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
// 如果key < node
if (node.left == null) {
node.left = new Node(key)
} else {
this.insertNode(node.left, key)
}
} else {
if (node.right == null) {
node.right = new Node(key)
} else {
this.insertNode(node.right, key)
}
}
}
}
const tree = new BinarySearchTree()
tree.insert(11)
tree.insert(7)
tree.insert(15)
tree.insert(5)
tree.insert(3)
tree.insert(9)
tree.insert(8)
tree.insert(10)
tree.insert(13)
tree.insert(12)
tree.insert(14)
tree.insert(20)
tree.insert(18)
tree.insert(25)
tree.insert(6)
以上代码利用类来实现对二叉树的创建。类外部定义了一个判断两个数大小关系的方法,便于统一维护与管理,最终这个外部方法也被引入到类中。
在实例化BinarySearchTree对象之后传入相关值时,会判断对象中是否已经存在节点,如果存在就用insertNode来为其插入子节点,如果不存在就创建一个根节点,在插入时,小于根节点的统一作为左侧子节点,大于根节点的统一作为右侧子节点,经过多次的递归调用之后创建除了如图的二叉树。
二叉树的遍历
二叉树在创建时使用了递归来创建出相应的子节点,他们有自己的层级,在遍历时同样需要使用递归的方式来遍历所有节点。
中序遍历
中序遍历是一种以上行顺序访问二叉树所有节点的遍历方法,可以按照从大到小的顺序访问所有节点。
// 中序遍历
inOrderTraverse(callback) {
this.inOrderTraverseNode(this.root, callback)
}
inOrderTraverseNode(node,callback){
if(node != null){
this.inOrderTraverseNode(node.left,callback)
callback(node.key)
this.inOrderTraverseNode(node.right,callback)
}
}
在类中添加两个方法,一个是inOrderTraverse,它接收一个回调函数,可以操作遍历到的节点,一个是inOrderTraverseNode方法,用于递归调用来遍历所有的节点
const printNode = (value) => console.log(value) tree.inOrderTraverse(printNode)
在调用inOrderTraverse方法之后,他会去调用inOrderTraverseNode方法,将创建的树和回调函数传入该方法,然后会判断节点存不存在,如果存在,将左侧的子节点再次传入该方法,一直递归调用,直到节点为Null时,输出当前节点,再输出该节点的父节点,以及右侧子节点,之后再往上输出祖父节点,以及对祖父节点的右侧子节点进行相同的操作,最终输出结果为:3,5,6,7,8,9,10,11,12,13,14,15,18,20,25
先序遍历
先序遍历是先访问父节点,再访问子节点的遍历方式,先序遍历的应用是可以打印一个结构化的文档。
// 先序遍历
preOrderTraverse(callback) {
this.preOrderTraverseNode(this.root, callback)
}
preOrderTraverseNode(node,callback){
if(node != null){
callback(node.key)
this.preOrderTraverseNode(node.left,callback)
this.preOrderTraverseNode(node.right,callback)
}
}
整体思路和中序遍历的思路几乎一样,区别只在于先对当前节点进行操作之后再去遍历他的左侧子节点,左侧子节点遍历完成之后再去遍历右侧子节点。
最终先序遍历的结果为:11,7,5,3,6,9,8,10,15,13,12,14,20,18,25
后序遍历
后续遍历是先访问节点的子节点,再访问节点本身的一种遍历方式,应用场景可以为计算一个目录及其子目录中所有文件所占空间的大小。
// 后序遍历
postOrderTraverse(callback) {
this.postOrderTraverseNode(this.root, callback)
}
postOrderTraverseNode(node,callback){
if(node != null){
this.postOrderTraverseNode(node.left,callback)
this.postOrderTraverseNode(node.right,callback)
callback(node.key)
}
}
后序遍历的结果为:3,6,5,8,10,9,7,12,14,13,18,25,20,15,11
二叉树中搜索方法
搜索最小值
以刚才创建的二叉树为例子,观察一下可以发现,最左侧的子节点即为最小子节点,因为,想要拿到最小子节点只需要拿到最左侧的节点即可。
min() {
return this.minNode(this.root)
}
minNode(node){
let current = node
while(current != null && current.left != null){
current = current.left
}
return current
}
当调用min方法时,会将树传递给minNode方法,并将树赋值给current,然后通过while循环来判断,如果当前节点不为空,并且左侧节点不为空的时候,就把左侧子节点传入下一个循环,最终就能拿到最左侧的节点,即为3
搜索最大值
搜索最大值与搜索最小值类似,只需要去拿出最右侧子节点即可。
max() {
return this.minNode(this.root)
}
maxNode(node){
let current = node
while(current != null && current.right != null){
current = current.right
}
return current
}
搜索指定值
搜索指定值和搜索最大最小值不太一样,但是我们在创建二叉树的时候有一个特性,凡是比父节点小的就作为左侧子节点,凡是比父节点大的就作为右侧子节点,利用这一特性可以很快的判断存不存在该指定的值。
search(key){
return this.searchNode(this.root,key)
}
searchNode(node,key){
if(node == null){
return false
}
if(this.compareFn(key,node.key) === Compare.LESS_THAN){
// 如果小于该节点就去左侧去子节点中找
return this.searchNode(node.left,key)
}else if(this.compareFn(key,node.key) === Compare.BIGGER_THAN){
// 如果大于该节点就去右侧子节点中找
return this.searchNode(node.right,key)
}else{
// 如果等于,直接返回结果
return true
}
}
删除某个节点
在删除某个节点时,唯一需要注意的就是,当删掉某个节点之后,他的子节点不能也跟着删除,需要给当前节点重新赋值,保证子节点的存在。
代码如下
// 移除节点
remove(key) {
this.root = this.removeNode(this.root,key)
}
removeNode(node,key) {
if(node == null) {
return null
}
if(this.cpmpareFn(key,node.key) === Compare.LESS_THAN) {
// 如果是左侧的,那么左侧的子树肯定要改变
node.left = this.removeNode(node.left,key)
return node
}else if(this.cpmpareFn(key,node.key) === Compare.BIGGER_THAN){
// 如果是右侧的那么右侧的子树肯定要改变
node.right = this.removeNode(node.right,key)
return node
}else{
// 如果相等就要对当前节点进行操作
// 如果当前节点的左右子节点都是null,直接将当前节点赋值为null,然后返回当前节点
if(node.left == null && node.right == null) {
node = null
return node
}
// 如果当前节点只有一侧子节点为null那么在移除当前节点之后,当前节点剩下的就是另一侧的子节点,直接赋值过来,改变指针指向就OK
if(node.left == null){
node = node.right
return node
}else if(node.right == null){
node = node.left
return node
}
// 左侧和右侧都有子节点的时候,需要移除当前节点,同时需要去拿一个值来放入这个位置,使其任然能够满足左侧子节点比他小,右侧子节点比他大的情况
const aux = this.minNode(node.right)
node.key = aux.key
node.right = this.removeNode(node.right,aux.key)
return node
}
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号