线段树

Part 1

\(\large\textbf{引入问题 }\text{ 其实就是洛谷 P3374}\)

你有一个长度为 n 的序列 a，有两种操作。
操作一：对序列 a 的一个数进行加值；
操作二：对序列 a 的一个区间的和进行询问。
数据范围：1 <= n,q <= 10^5，q 代表操作次数。

查询区间和可以使用前缀和，但是对区间 \([l,r]\) 加值需要影响到前缀和数组的 \([l,n]\)。

故区间修改的复杂度为 \(\mathcal O(n)\)，而查询是 \(\mathcal O(1)\) 的。所以总的时间复杂度为 \(\mathcal O(nq)\)，不能通过此题。

Part 2

线段树是一种傻逼的数据结构，它的每一个结点代表了一个区间。

而根节点代表的区间是 \([1,n]\)，它的两个子结点分别存储的是 \([1,1+n/2]\) 和 \([1+n/2 + 1, n]\)。

如下图：

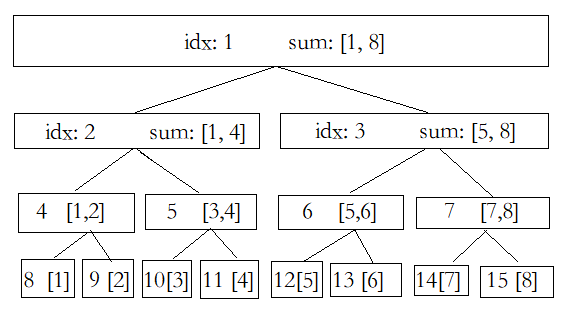
idx 代表结点编号，sum 代表的是当前区间的和。

\(\large\textbf{建树}\)

从这棵树上很容易看得出来，每个结点的 sum 值等于它子节点的 sum 值之和。

若当前节点是叶子结点，当前的 sum 值就是序列 \(a\) 的值。

void build(int k, int l, int r)     //参数：当前结点编号，当前编号的区间左右端点
{
	if (l == r) {                   //遇到叶子结点时，退出建树
		tree[k] = a[l];
		return ;
	}
	int mid = l + r >> 1;           //等同于 l + r / 2
	build(k << 1, l, mid);          //构建左子树，k << 1 等同于 k * 2
	build(k << 1 | 1, mid + 1, r);  //构建右子树，k << 1 | 1 等同于 k * 2 + 1
	tree[k] = tree[k<<1] + tree[k<<1 | 1];   //构建完子树后更新当前结点的值
}

\(\large\textbf{单点加}\)

例如我们在把 \(a_6\) 加上 \(v\) 时，受到影响的结点编号为 \(1,3,6,13\)，只要找到这四个结点，把它们的值都加上 \(v\) 即可。

如何找到这几个结点呢？

可行的方法是：

1. 若当前区间中包含了需要加值的下标，则递归左子树和右子树；
2. 若当前区间不包含需要加值的下标，则直接退出；
3. 若当前区间和需要加值的下标重合，则直接修改此区间。

void modify(int k, int l, int r, int p, int v) //参数：当前结点编号，当前编号的区间左端点和右端点，需要修改的下标，需要加的值
{
	if (l > p || r < p) return ;     //不包含 p 点
	if (l == p && r == p) {          //当前区间就是 p 点
		tree[k] += v;
		return ;
	}
	
	int mid = l + r >> 1;
	modify(k << 1, l, mid, p, v);    //递归左子树
	modify(k << 1 | 1, mid + 1, r, p, v);  // 递归右子树
	tree[k] = tree[k<<1] + tree[k<<1 | 1]; //别忘了更新当前的和
}

\(\large\textbf{查询区间和}\)

例如查询 \([2,8]\) 的和，只需要知道结点编号为 \(9,5,3\) 的值，并把它们加在一起即可。

查找这些区间的方法可以参考单点加。

long long query(int k, int l, int r, int x, int y) //参数：当前节点编号，当前结点的左右端点，查询区间的左右端点
{
	if (x <= l && y <= r) return tree[k];  //当前结点完全在查询区间中
	if (l > y || r < x) return 0;          //当前结点完全不在查询区间中，返回的是一个不影响答案的数，因为此问题求的是区间和，所以返回 0 不影响答案
	
	int mid = l + r >> 1;
	return query(k<<1, l, mid, x, y) + query(k<<1|1, mid+1, r, x, y); //返回左右子树的结果
}

这样，修改单点的复杂度为 \(\mathcal O(\log n)\)，查询也是 \(\mathcal O(\log n)\)，可以通过此题。

练手：洛谷 P3374（虽然是树状数组，但是可以用线段树解），洛谷 P1351（这是维护区间最大值的模型，和维护区间和有些不同）。

Part 3

那区间加值、区间查询改如何做呢？

如果我们按单点加值的思想，把这个区间的每一个点全部加上一个数，那么复杂度会翻倍；

\(\large\textbf{懒惰标记}\)

还有一种方法是在加值时，直接找到对应的区间，把这个区间连同它的所有子树全部加上一个数，那么时间复杂度也承受不住。

可以考虑在加值时，仅仅把当前的结点加上一个值，不把子树加值，等到下次访问到这个结点时顺便加上子树，这样可以很好地优化复杂度。

下次访问时，我们如何知道我该把它的子树加上多少？可以考虑个这个结点打上一个标记，标记代表这个结点已经被加上了某个值。

记第 \(i\) 个结点的加值标记为 \(add_i\)，这个给结点的子树加上值的过程叫标记下传，这个标记被称作Lazy tag，即懒惰标记。

没听懂的举个例子：有一个区间 \(a\)，初始值全为 \(0\)，我现在要给区间 \([2,6]\) 加上 \(4\)，然后再查询区间 \([4,7]\) 的和。

下图中的第一个参数代表结点编号，第二个参数代表区间和，第三个参数代表当前结点的懒标记。

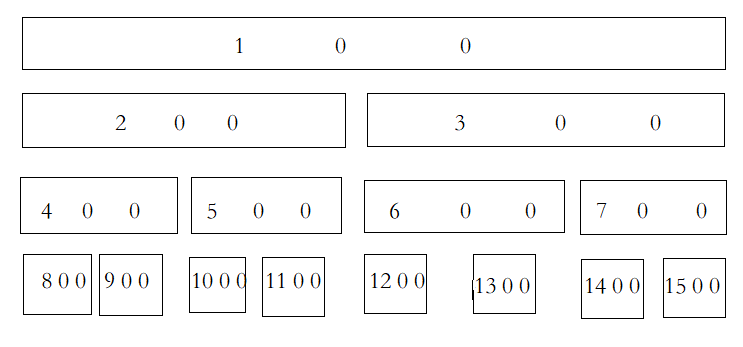
加值，在结点 \(9,5,6\) 加上 \(4\) 并把懒标记打上 \(4\)：

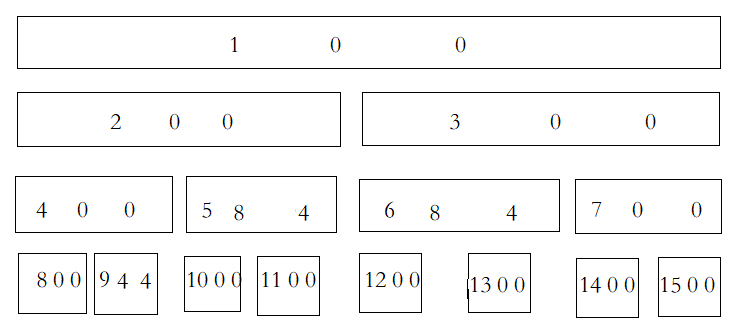
然后查询，查到了结点 \(11,6,14\)，在查询过程中已经把结点 \(5,6\) 的标记下传到 \(10,11,12,13\) 处，并在这四个结点处加值：

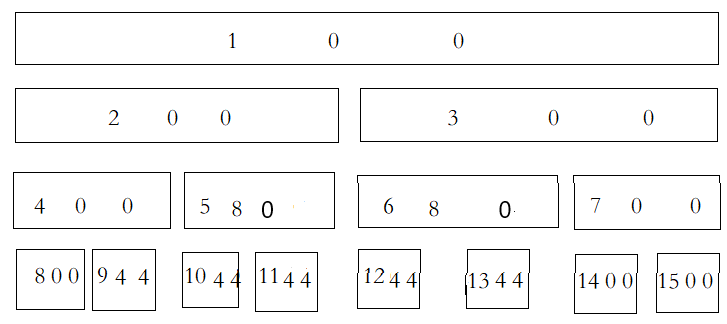
然后结果就是结点 \(11,6,14\) 的和，为 \(4+8+0=12\)。在查询的同时也下传了标记。

\(\large\textbf{加值并打标记操作}\)

void Add(int k, int l, int r, int v)  //给结点 k 加上 v，结点 k 的区间为 [l,r]
{
	tree[k] += (r-l+1) * (long long) v;   //区间所有数都加 v，则区间和加 (r-l+1)*v
	add[k] += v;                          //打标记
}

\(\large\textbf{标记下传操作}\)

void pushdown(int k, int l, int r, int mid)     //下传编号为 k 的标记
{
	if (!add[k]) return ;      //没有标记就不用下传
	Add(k<<1,l,mid,add[k]);    //下传左子树
	Add(k<<1|1,mid+1,r,add[k]);//下传右子树
	add[k] = 0;                //清空此结点的标记
	return ;
}

\(\large\textbf{区间修改 / 区间查询}\)

和上面单点修改 / 区间查询的代码没什么不同，就是加了个下传标记：

void modify(int k, int l, int r,int x, int y, int v) //给区间 [x,y] 加上 v
{
	if (x <= l && r <= y)
	{
		Add(k,l,r,v);
		return ;
	}
	if (l > y||r<x) return ;
	int mid =l +r>>1;
	pushdown(k,l,r,mid);   //标记下传
	modify(k <<1,l,mid,x,y,v);
	modify(k<<1|1,mid+1,r,x,y,v);
	tree[k] = tree[k<<1] + tree[k<<1|1];
	return ;
}

long long query(int k, int l, int r,int x, int y)
{
	if (x<=l&& r<=y) return tree[k];
	if (l>y ||r<x) return 0;
	int mid = l + r >> 1;
	pushdown(k,l,r,mid);           //标记下传
	
	return query(k<<1,l,mid,x,y) + query(k<<1|1,mid+1,r,x,y);
}

Part 4

练习：

• 洛谷 P3372 区间加 / 查询，模板。
• 洛谷 P1253 区间加 / 修改 / 区间查询，注意不同的 tag 会互相影响。
• 洛谷 P3373 区间加 / 乘 / 区间查询，注意不同的 tag 会互相影响。

推荐题单

Part 5 （及其重要）

看了这么久，点个赞再走呗 \(\sim\)