密码学

密码学家研究的主要技术

(1) 对称密码

(2) 公钥密码

(3) 单向散列函数

(4) 消息认证码

(5) 数字签名

(6) 伪随机数生成器

可用如下图示解释

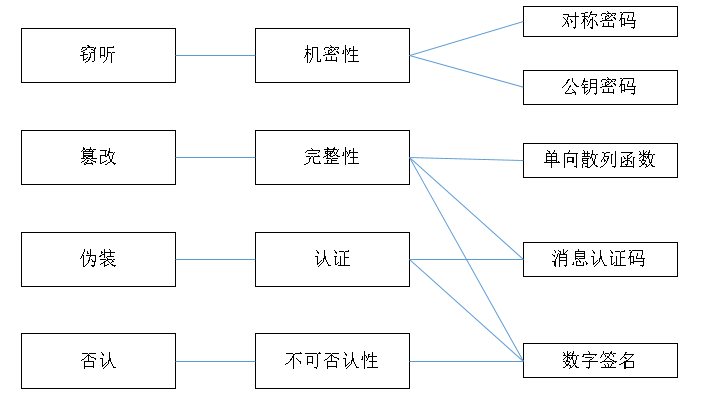
加密算法分对称加密算法与非对称加密算法。

对称分组密码

非对称加密算法

数据加密标准(Data Encryption Standard, DES)

三重数据加密标准(Triple DES, 3DES)

高级加密标准(Advanced Encryption Standard, AES)

RSA

Diffie-Hellman

DSA

ECC

SM2

RSA 、ECC既可以用于加/解密数据，也可以用于密钥交换，也可以用于数字签名。
DH算法一般来说只能用于密钥交换。
DSA算法则是专用于数字签名的算法。
SM2国标算法

对称加密模型

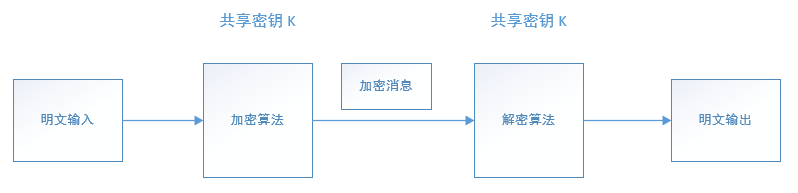
为解决密钥配送的问题

* 通过事先共享密钥来解决

* 通过密钥分配中心来解决

* 通过Diffie-Hellman密钥交换来解决

* 通过公钥密码来解决

非对称密钥算法

RSA 算法一般用来

* 密钥交换

* 数字签名

也可以用于加密数据，因加密速度慢，一般不用做大量的数据加密。

使用openssl生成RSA密钥

参考链接 https://www.openssl.org/docs/manmaster/man1/genrsa.html

openssl genrsa 
　　　　 [-help]    打印帮助信息 
　　　　 [-out filename]  -out 输出文件名
　　　　 [-passout arg]   -passout 加密RSA密钥
        [-aes128] [-aes192] [-aes256] [-aria128] [-aria192] [-aria256] [-camellia128] [-camellia192] [-camellia256] [-des] [-des3] [-idea]  加密RSA密钥的算法
        [-f4] [-3]  指数选项 -f4（值为 65537， 默认） 或 3(值为3)
        [-rand file...] [-writerand file] [-engine id] [-primes num] 
        [numbits]  密钥长度

可配置参数

* RSA 输出密钥文件名

* RSA 密钥文件是否是加密

* RSA 密钥长度

例子1：使用OpenSSL 生成RSA密钥

要求输出文件名为Client.Key

密钥长度为1024个字节

# openssl genrsa -out client.key 1024
Generating RSA private key, 1024 bit long modulus
..............++++++
....++++++
e is 65537 (0x10001)

查看生成的RSA文件

# cat client.key 
-----BEGIN RSA PRIVATE KEY-----
MIICXQIBAAKBgQDLUzbPSNQOC25Idro5MTud9Wv+JRBaZDQt5/Ue2E5+icpGfKgz
MLjj7FHUA/AwlgoDiUF+MEgv7dvF623k1BeW8+/d/uMx9equZ4gkCkqgqIc02698
G1y1g/kszB9loRLQYVKaizg2Sb+ULeK01G7Yesn+tLNsmljjeh40qlp0AwIDAQAB
AoGAM5cwwBXVoJ6r4/0kMWDZpLHiLgFPjfABAWjq3GG8QQVLauk0cJC7STHsbWR2
bI2ViuIn2RH9LxQmgKjFIJvkQ/foeFnT9VjIIdqUSu5Yy/RUCcPf9w3JE1cP+nMJ
HAbbf8cS5UsQ3zs5RiuLVyBSwedp0jjVWopr4S7/tKc2bPkCQQD6TqR3o1ty7Moo
xgUvARshvAnpaMFkqk4uyjEEzvHUOB4ds97ynjeCTZfFDQTr0WRkAdZvYbBAap1w
v1a4bganAkEAz/MHVjJhVJ2CqXkEqQMSBHoRCc2+Jom+ewTe8aQvBExYqFprotoY
NbXbBWBiRyQP4bRxM4OX/gRyusQ3W/YvRQJBAOrLCCWdW3PjQAKdNVGRJQUw4M9M
T1SBGBN14CNVh6x882sDRZep6AHXjQzvGHWoFhZlTuNt7CmQmJyhLtSTiLMCQQC9
/kgHw0QWMUs+WCmf2gROPtDuaiJ/x35Xm52undmvTan7N5H8WtOfzyXrhaKFaTdx
epGrBWKLXbkNV1VVGlsZAkAm/MJ73VW/+yS8HYPLsM+EqbIqtIqrkW4n4LUex+hl
9VQEQRuj2IR6xYHhq83YDMQkVNq6FdFy4MDq9ucEnatE
-----END RSA PRIVATE KEY-----

例子2：使用OpenSSL 生成加密RSA文件

要求

输出文件名为 clientenc.key

使用des3加密算法

密码为weiwei

密钥长度为1024位

# openssl genrsa  -out clientenc.key -des3 -passout pass:weiwei 1024
Generating RSA private key, 1024 bit long modulus
.........++++++
...........................................................................................................++++++
e is 65537 (0x10001)

# cat clientenc.key 
-----BEGIN RSA PRIVATE KEY-----
Proc-Type: 4,ENCRYPTED
DEK-Info: DES-EDE3-CBC,6D0FB82EE1B256FF

5lBP5/AG0YMBmx7Xg2YF2JgEZG8sXPqgViJ02R03p/YMMhtgFLm4UeBtp0Us56qd
0Uf/+i7f2yAtFKSPeu8sElp5daQvdmNokjbzYJDsdY2dmdp4Tr5cJvvLqw83y6xS
tLdhZPCAgdvaSd8qld5zRU53f3A1UKaniqfaeYef6T6vsbwgjcxDYpp+bjMY6bZM
zQuf0rg5D9ZaYhpKoZq8dtXPrPs/x6wiumjC6Ti3natcTl0DHwpn9bT2Ekiacx1W
Z6RB3X8Ai7bTCTvTvN/pGxPg65y96wDkkgkiLqQiw3nxWK6xnBEk9BVoYsuQCt8y
0S81rZ3e44JNNAcCf/MXfOk2yRrXE3LLbODslRr81+uUe5quo+PAakYffU547a6j
aY+q4GbsngMK6Gh8dDROF+ixsJo1ikZIrz4kODUmc+lII2tFACj5VS8x7v2ogJyN
m2gvFlcskBSP9075Rp0nmrhGG7/FRZyRn02RPj8DhgiNSkWIZFfCLXw/GJ+4VqkE
QkPrzt8sF0SgrRP+gPgb8koxHy7S5sEnRHhGkum477PcvVcawTaAcjgeeHzsQmz3
lp3NMZLCzQCBflHYJ8ZPsldjcYhOULjoHIKpCJ7VUgwTSDCkKyN6I9EQMUe1jiOV
P8jQqRY/ZmZOaXdPWKcuH47bHiQe2IeUC6TwVBA6qanLm5O6A66TlMXVlAYX2j2e
c95wqEtEamjBKPd6os5fcSorFFsqhpDdy35yvQNo6a+pU4/DK+B+0fm9KkaQPthZ
OxfQWwWLVXpi/Z1EgnH0cgbt3gJjD/CoYV07pyRj5AxsZ3UGxG36WA==
-----END RSA PRIVATE KEY-----

RSA 使用openssl库的实现

RSA 密钥包含三个部分：公钥指数，私钥指数，模数 e
第一步：分别保存好三个数，其中私钥指数与模数都是大素数
第二步：构造公钥与私钥RSA结构
第三步：利用构造的RSA结构的指针进行公钥加密-私钥解密或者
公钥解密-私钥加密

/* 
 * file:        genrsa.c                                      
 * purpose:     Example code for creating RSA key pairs         
 * author:      06/29/2018 Qiwei                             
 *                                                              
 * gcc -o genrsa genrsa.c -lssl -lcrypto              
 */

#include <stdio.h>
#include <openssl/rsa.h>
#include <openssl/pem.h>

int main(int argc, char* argv[]) 
{
    int             ret = 0;
    RSA             *rsa = RSA_new();
    BIGNUM             *bn = BN_new();
    BIO             *bp_public = NULL;
    BIO                *bp_private = NULL;
    int             bits = 2048;               /* RSA密钥长度 */
    unsigned long   e = RSA_F4;                   /* 模数e */
 
    if (bn == NULL || rsa == NULL) {
        ret = 1;
        goto end;
    }
    
    /* 1. generate rsa key */
    if (!BN_set_word(bn, e) || !RSA_generate_key_ex(rsa, bits, bn, NULL)) {
        ret = 1;
        goto end;
    }
        
    /* 2. save public key */
    bp_public = BIO_new_file("public.pem", "w+");
    ret = PEM_write_bio_RSAPublicKey(bp_public, rsa);
    if(ret != 1){
        goto end;
    }
 
    /* 3. save private key */
    bp_private = BIO_new_file("private.pem", "w+");
    ret = PEM_write_bio_RSAPrivateKey(bp_private, rsa, NULL, NULL, 0, NULL, NULL);
 
    /* 4. free */
end:
    BIO_free_all(bp_public);
    BIO_free_all(bp_private);
    BN_free(bn);
    RSA_free(rsa);
    
    return (ret);
}

Diffie-Hellman 算法

参考文档 https://www.openssl.org/docs/manmaster/man1/dhparam.html

ECC 算法

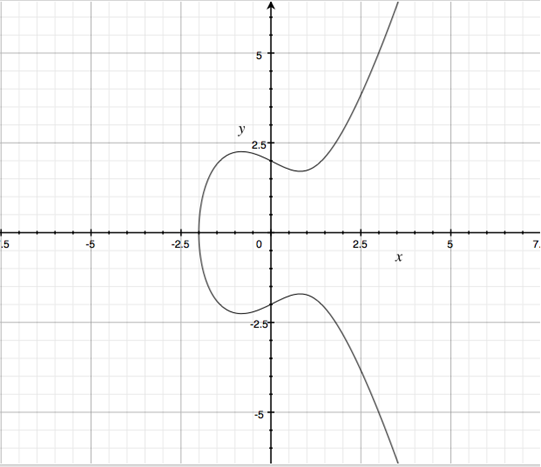
椭圆曲线上的离散对数问题：
已知
椭圆曲线E
椭圆曲线E上一点G（基点）
椭圆曲线E上的一点xG（x倍的G）
求解
x

ECC 优点
* 生成密钥速度更快
* 密钥内容更小

openssl ecparam 
    [-help] 
    [-inform DER|PEM] [-outform DER|PEM]   输入与输出格式，默认PEM
    [-in filename] [-out filename]  输入与输出文件名
    [-noout]  不打印ec参数
    [-text]   以文本方式打印ec参数
    [-C]      以C函数方式打印参数
　　 [-check]  验证ec参数
    [-name arg] 
    [-list_curves] 
    [-conv_form arg] 
    [-param_enc arg] 
    [-no_seed] 
    [-rand file...] 
    [-writerand file] 
    [-genkey]   生成ec密钥
    [-engine id]

列表当前所支持 ec 长度

# openssl ecparam  -list_curves
  secp256k1 : SECG curve over a 256 bit prime field
  secp384r1 : NIST/SECG curve over a 384 bit prime field
  secp521r1 : NIST/SECG curve over a 521 bit prime field
  prime256v1: X9.62/SECG curve over a 256 bit prime field

使用案例

openssl ecparam -out ecckey.pem -name prime256v1 -genkey

# cat ecckey.pem
-----BEGIN EC PARAMETERS-----
BggqhkjOPQMBBw==
-----END EC PARAMETERS-----
-----BEGIN EC PRIVATE KEY-----
MHcCAQEEIJqXNSvRphWnpKXg/RKGf5vzkb/emTaVIvWFiu8iK37uoAoGCCqGSM49
AwEHoUQDQgAExRqYLPjN9nIAkvJ+CoVS5tC3kKGels2hGfqMGUQvKOYQMAyF83BA
RqzhccdmPVaHa0LGgU6322M1t7BN+n5IAQ==
-----END EC PRIVATE KEY-----

/* 
 * file:        genecc.c                                      
 * purpose:     Example code for creating elliptic curve         
 * author:      06/29/2018 Qiwei                             
 *                                                              
 * gcc -o genecc genecc.c -lssl -lcrypto              
 */
 
#include <openssl/bio.h>
#include <openssl/err.h>
#include <openssl/ec.h>
#include <openssl/pem.h>

#define ECCTYPE    "prime256v1"

int main(int argc, char* argv[]) 
{

  BIO               *outbio = NULL;
  EC_KEY            *myecc  = NULL;
  EVP_PKEY          *pkey   = NULL;
  int               eccgrp;
  int                 ret = 0;

  /* Create a EC key sructure, setting the group type from NID  */
  eccgrp = OBJ_txt2nid(ECCTYPE);
  myecc = EC_KEY_new_by_curve_name(eccgrp);

   /* For cert signing, we use  the OPENSSL_EC_NAMED_CURVE flag*/
  EC_KEY_set_asn1_flag(myecc, OPENSSL_EC_NAMED_CURVE);

  /* Create the public/private EC key pair here               */
  if (! EC_KEY_generate_key(myecc)) {
    goto end;
    BIO_printf(outbio, "Error generating the ECC key.");
  }
  
   /*  
    * Converting the EC key into a PKEY structure let us
    *  handle the key just like any other key pair.             
    */
  pkey=EVP_PKEY_new();
  if (!EVP_PKEY_assign_EC_KEY(pkey,myecc)) {
      BIO_printf(outbio, "Error assigning ECC key to EVP_PKEY structure.");  
      goto end;
  }
    
  /* 
   * Now we show how to extract EC-specifics from the key     
   */
  myecc = EVP_PKEY_get1_EC_KEY(pkey);
  const EC_GROUP *ecgrp = EC_KEY_get0_group(myecc);

  /* Create the Input/Output BIO's */
  outbio  = BIO_new(BIO_s_file());
  outbio = BIO_new_fp(stdout, BIO_NOCLOSE);
  
  /* 
   * Here we print the key length, and extract the curve type.  
   */
  BIO_printf(outbio, "ECC Key size: %d bit\n", EVP_PKEY_bits(pkey));
  BIO_printf(outbio, "ECC Key type: %s\n", OBJ_nid2sn(EC_GROUP_get_curve_name(ecgrp)));

  /* 
   * Here we print the private/public key data in PEM format.   
   */
  if(!PEM_write_bio_PrivateKey(outbio, pkey, NULL, NULL, 0, 0, NULL)) {
    BIO_printf(outbio, "Error writing private key data in PEM format");
    goto end;
  }


  if(!PEM_write_bio_PUBKEY(outbio, pkey)) {
    BIO_printf(outbio, "Error writing public key data in PEM format");      
  }

end:
  EVP_PKEY_free(pkey);
  EC_KEY_free(myecc);
  BIO_free_all(outbio);

  return ret;
}

DSA 算法

只能用于数据签名

posted @ 2018-05-29 15:05 elewei 阅读(1114) 评论(0) 收藏举报

刷新页面返回顶部

David

密码学