2021.06.24 树状数组

树状数组的前置知识

1.负数存法

至于定义，请百度百科

2.如何找出最低位的1

首先，定义lowbit()为查询最低位1的函数，如二进制的1111001000，则其乘-1为0000111000（如果我没写错的话），则这两个数后四位是一样的，用&就可以求出这四位一样的数的值。代码如下：

int lowbit(int x){
	return x&-x;
}

3.差分以及前缀和

一维树状数组

单点修改，区间查询洛谷3374

正常的从下到上不断修改就可以，查询的时候从上到下不断查询，有必要可以想一想前缀和

单点修改代码如下：

void add(int x,int k){
	while(x<=n){
		tree[x]+=k;
		x+=lowbit(x);
	}
}

还可以写为：

void add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i))tree[i]+=k;
}

区间查询代码如下：

int sum(int x){
	int ans=0;
	while(x){
		ans+=tree[x];
		x-=lowbit(x);
	}
	return ans;
}

还可以写为：

int sum(int x){
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))ans+=tree[i];
}

区间修改，单点查询洛谷3368

使用差分即可。完整代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int aa=5e5+10;
int n,m,a[aa];
ll tree[aa];
inline int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')w=-1;
		ch=getchar();
	}
	while(ch<='9'&&ch>='0'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s*w;
}
int lowbit(int x){
	return x&-x;
}
void add(int x,int k){
	while(x<=n){
		tree[x]+=k;
		x+=lowbit(x);
	}
}
int sum(int x){
	ll ans=0;
	while(x){
		ans+=tree[x];
		x-=lowbit(x);
	}
	return ans;
}
int main(){
	n=read();m=read();
	for(int i=1;i<=n;i++)a[i]=read();
	for(int i=1;i<=m;i++){
		int op;
		op=read();
		if(op==1){
			int u,v,k;
			u=read();v=read();k=read();
			add(u,k);add(v+1,-k);
		}else{
			int u;
			u=read();
			cout<<a[u]+sum(u)<<endl;//也可以在一开始就把数组a中的数用差分给存到树状数组里面
		}
	}
	return 0;
}

区间修改，区间查询 LOJ#132

我不明白为什么。为了写这篇博客，我彻底理解了。——2021.06.24 13:03

从我自己的理解是前缀和+差分。tree[]是差分数组，记录的是编号为i的结点上的差分的总结果，那么如何用前缀和来计算呢？

首先来思考一下小学学过的凑整法。

\[99*99=（100-1）*99=100*99-99 \]

接下来深入思考一下。当我们要求前X个数之和，已知从Xi个数开始都加了Ki，一共有n对对应的Xi与Ki；

\[ans=K1*(X-X1+1)+K2*(X-X2+1)+...+Kn*(X-Xn+1) \]

\[ans=K1*(X+1)-K1*X1+K2*(X+1)-K2*X2+..+Kn*(X+1)-Kn*Xn \]

\[ans=(X+1)*(K1+K2+..+Kn)-(K1*X1+K2*X2+..+Kn*Xn) \]

瞧一瞧，如何求前缀和就不用说了吧？

int sum(int x){
	ll ans=0;
	for(int i=x;i>0;i-=lowbit(i))
	ans+=(x+1)*tree[i]-num[i];
	return ans;
}

完整代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long 
const int aa=1e6+10;
typedef long long ll;
int n,m,a[aa];
ll tree[aa],num[aa];
inline int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')w=-1;
		ch=getchar();
	}
	while(ch<='9'&&ch>='0'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s*w;
}
int lowbit(int x){
	return x&-x;
}
void add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i)){
		tree[i]+=k;
		num[i]+=(ll)x*k;
	}
}
int sum(int x){
	ll ans=0;
	for(int i=x;i>0;i-=lowbit(i))
	ans+=(x+1)*tree[i]-num[i];
	return ans;
}
signed main(){
	n=read();m=read();
	for(int i=1;i<=n;i++){
		a[i]=read();
		add(i,a[i]-a[i-1]);
	}
	for(int i=1;i<=m;i++){
		int op;
		op=read();
		if(op==1){
			int u,v,k;
			u=read();v=read();k=read();
			add(u,k);add(v+1,-k);
		}else{
			int u,v;
			u=read();v=read();
			cout<<sum(v)-sum(u-1)<<endl;
		}
	}
	return 0;
}

二维树状数组

前置知识

从小学数学题开始出发，已知在方格纸中有两点坐标(x,y),(u,v),每个方格中有一个数字，求以这两点为直角顶点的小长方形中的数字之和是多少？

说简单点就是下图右上角小长方形内个数字之和是多少？（当然，为了方便起见，我并没有画数字与格子）

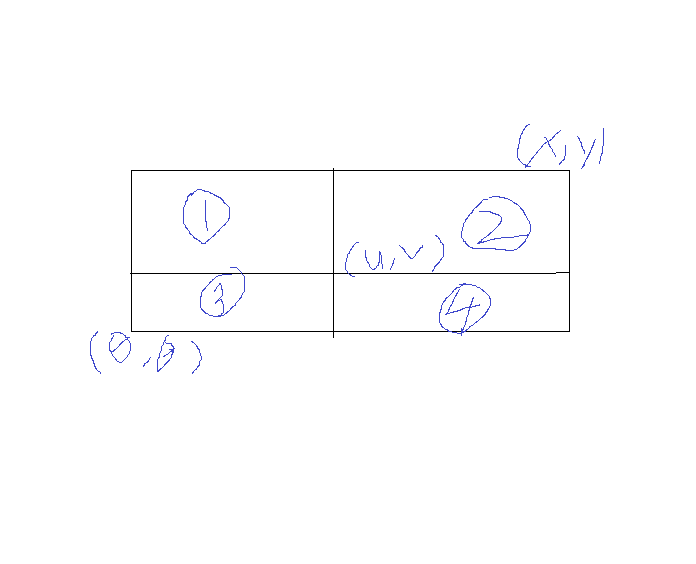
总面积为S1+S2+S3+S4，左半部分面积为S1+S3，下半部分面积为S3+S4，则2的面积为S2=(S1+S2+S3+S4)-(S1+S3)-(S3+S4)+S3。（把数字和用面积代替一下，反正都是那种意思）

接下来步入正题。

单点修改，区间查询 LOJ#133

直接上完整代码吧。

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int aa=5000;
int n,m,tree[aa][aa];
inline int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')w=-1;
		ch=getchar();
	}
	while(ch<='9'&&ch>='0'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s*w;
}
int lowbit(int x){
	return x&-x;
}
void add(int x,int y,int k){
	for(int i=x;i<=n;i+=lowbit(i)){
		for(int j=y;j<=m;j+=lowbit(j))
		tree[i][j]+=k;
	}
}
int sum(int x,int y){
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i)){
		for(int j=y;j>0;j-=lowbit(j))
		ans+=tree[i][j];
	}
	return ans;
}
signed main(){
	n=read();m=read();
	int op;
	while(~scanf("%lld",&op)){
		if(op==1){
			int u,v,k;
			u=read();v=read();k=read();
			add(u,v,k);
		}else if(op==2){
			int u,v,x,y;
			u=read();v=read();x=read();y=read();
			cout<<sum(x,y)-sum(x,v-1)-sum(u-1,y)+sum(u-1,v-1)<<endl;
		}
	}
	return 0;
}

区间修改，单点查询 LOJ#134

依旧运用差分的思想（废话，总不能一个点一个点地去修改吧？），设差分数组为d[ ] [ ],原数组为a[ ] [ ]

二维前缀和为

\[sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j] \]

则差分为

\[cha[i][j]=a[i][j]-a[i][j-1]-a[i-1][j]+a[i-1][j-1] \]

例如：

 1  4  8                     1  3  4
 6  7  2   对应的差分数组为    5 -2 -9
 3  9  5                    -3  5  1

当然，上面一坨式子可以扔一边。在零矩阵中，我们想要给一个小矩阵加x，则

0  0  0  0  0  0  0
0  x  0  0  0 -x  0
0  0  0  0  0  0  0
0  0  0  0  0  0  0
0 -x  0  0  0  x  0
0  0  0  0  0  0  0

原数组变为

0  0  0  0  0  0  0
0  x  x  x  x  x  0
0  x  x  x  x  x  0
0  x  x  x  x  x  0
0  x  x  x  x  x  0
0  0  0  0  0  0  0

欸，只查询单点的话，是不是代码应该和上一个代码相似？

完整代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int aa=1e4+10;
int n,m,tree[aa][aa];
inline int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')w=-1;
		ch=getchar();
	}
	while(ch<='9'&&ch>='0'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s*w;
}
int lowbit(int x){
	return x&-x;
}
void add(int x,int y,int k){
	for(int i=x;i<=n;i+=lowbit(i))
		for(int j=y;j<=m;j+=lowbit(j))
		tree[i][j]+=k;
}
int sum(int x,int y){
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))
		for(int j=y;j>0;j-=lowbit(j))
		ans+=tree[i][j];
	return ans;
}
signed main(){
	n=read();m=read();
	int op;
	while(~scanf("%lld",&op)){
		if(op==1){
			int u,v,x,y,k;
			u=read();v=read();x=read();y=read();k=read();
			add(u,v,k);add(u,y+1,-k);
			add(x+1,v,-k);add(x+1,y+1,k);
		}else{
			int u,v;
			u=read();v=read();
			cout<<sum(u,v)<<endl;
		}
	}
	return 0;
}

区间修改，区间查询 LOJ#135

还记得一维树状数组如何进行区间修改、区间查询的吗？类比一下~

设在点(x,y)上的数为ans，差分数组为cha[ ] [ ],则从点(0,0)到点(x,y)的前缀和很容易求出来。

首先求出每个点上的值：

\[ans=cha[1][1]+cha[1][2]+...+cha[1][x]+cha[2][1]+cha[2][2]+...+cha[2][x]+...+cha[x][y] \]

则从点(0,0)到点(x,y)的前缀和为：

\[cha[1][1]*(x-1+1)*(y-1+1)+cha[1][2]*(x-2+1)*(y-2+1)+...+cha[x][y]*(x-x+1)*(y-y+1) \]

\[cha[1][1]*((x+1)*(y+1)-1*(y+1)-1*(x+1)+1*1)+cha[1][2]*((x+1)*(y+1)-1*(y+1)-2*(x+1)+1*2)+...+cha[x][y]*((x+1)*(y+1)-x*(y+1)-y*(x+1)+x*y) \]

设i>=1&&i<=x,j>=1&&j<=y，则

\[cha[i][j]*((x+1)*(y+1)-i*(y+1)-j*(x+1)+i*j) \]

\[(x+1)*(y+1)*cha[i][j]-(y+1)*(cha[i][j]*i)-(x+1)*(cha[i][j]*j)+(cha[i][j]*i*j) \]

我们可以开四个数组来维护

\[t1[i][j]=cha[i][j] \]

\[t2[i][j]=cha[i][j]*i \]

\[t3[i][j]=cha[i][j]*j \]

\[t4[i][j]=cha[i][j]*i*j \]

完整代码如下：

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define int long long
const int aa=5e3;
int n,m,t1[aa][aa],t2[aa][aa],t3[aa][aa],t4[aa][aa];
inline int read(){
	int s=0,w=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')w=-1;
		ch=getchar();
	}
	while(ch<='9'&&ch>='0'){
		s=s*10+ch-'0';
		ch=getchar();
	}
	return s*w;
}
int lowbit(int x){
	return x&-x;
}
void add(int x,int y,int k){
	for(int i=x;i<=n;i+=lowbit(i))
		for(int j=y;j<=m;j+=lowbit(j)){
			t1[i][j]+=k;
			t2[i][j]+=k*x;
			t3[i][j]+=k*y;
			t4[i][j]+=k*x*y;
		}
}
int sum(int x,int y){
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i))
		for(int j=y;j>0;j-=lowbit(j)){
			ans+=(x+1)*(y+1)*t1[i][j]-(y+1)*t2[i][j]
				-(x+1)*t3[i][j]+t4[i][j];
		}
	return ans;
}
signed main(){
	n=read();m=read();
	int op;
	while(~scanf("%lld",&op)){
		if(op==1){
			int u,v,x,y,k;
			u=read();v=read();x=read();y=read();k=read();
			add(u,v,k);add(u,y+1,-k);
			add(x+1,v,-k);add(x+1,y+1,k);
		}else{
			int u,v,x,y;
			u=read();v=read();x=read();y=read();
			cout<<sum(x,y)-sum(x,v-1)-sum(u-1,y)+sum(u-1,v-1)<<endl;
		}
	}
	return 0;
}

posted on 2021-06-26 07:34 eleveni 阅读(88) 评论(0) 收藏举报

刷新页面返回顶部