TMSP蒸气压温度曲线之拟合

为了填写化学品的《安全周知卡》蒸气压的数据, 同事反映找不到这个物质在25℃下的蒸气压值. 我在CA数据库中查了一下 三(三甲基硅基)磷酸酯(TMSP). 果然没有常温下的蒸气压数据. 它是有很多不同压力下的沸点数据,经过粗处理后如下:

沸点/℃	压强/mmHg
49	0.2
58	1.5
67.5	0.5
77	4
86	4
86	4
92	5
95.5	7
97	6
100	6
105	10.5
110	12
110	4
228	720
231.8	749.5

我们知道,一种液体在某一压强P下的沸点t, 换种表达方式就是, 它在这个温度t下,它的饱和蒸气压就是这个压强P. 比如说,水在760mmHg下的饱和蒸气压, 就是1个大气压. 再加热升高温度,蒸气压超过1个大气压,蒸气压大于外界气压, 水就沸腾了,沸腾吸热快,水温就下来了.从而达到一个平衡. 如果在高原地区,外界气压小了, 温度不用到100℃水的蒸气压就能大于外界气压,达到沸腾状态,这也就是低压下沸点变低的现象。不单是水, 其它液体也遵守这个规律.

理解了上面的原理，我们可以说，以上不同压强下的沸点，实际上也是不同温度下该物质的蒸气压。根据这些蒸气压，我们就可以进行数据的回归分析了。依据还是使用安托宁方程:

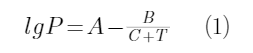
在回归之前,需要对数据进行一些预先处理. 先对温度列进行排序,从低到高. 再转化成绝对温度T (=273.15+ ℃ ) 和lgP(P的单位统一用KPa, 1 Torr=1mmHg=0.1333KPa):

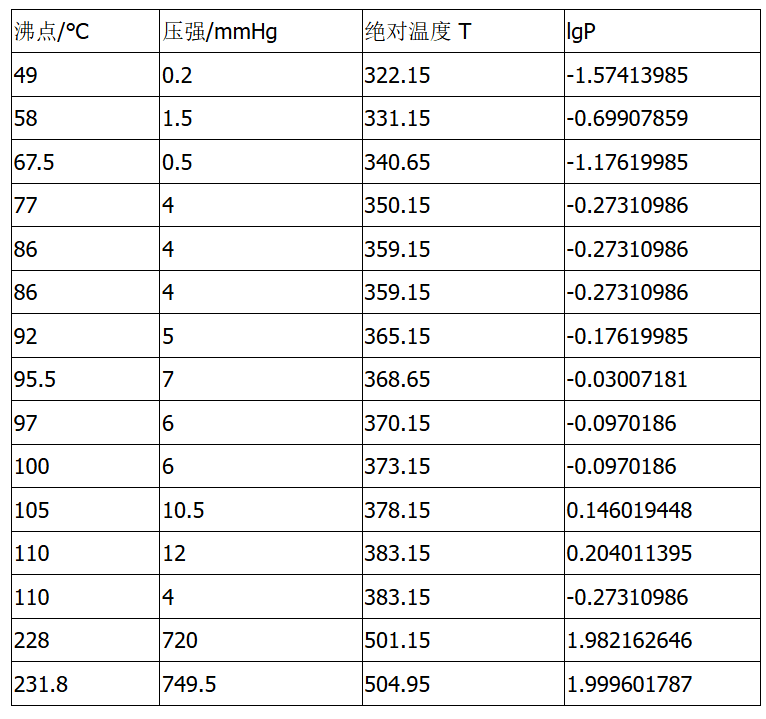
在Excel中对lgP和K值作散点图， 初步看看数据的分布情况。 这一步很重要，由于数据的来源质量不一样， 需要进行初步的数据筛选，以去除明显不合理的数据， 否则可能出现拟合无优化解的情况。特别是数据量很少的情况下，对异常值尤为敏感。 这组数据还不错， 回归出来效果不错.

将数据另存为data.txt来方便Python程序导入.处理的代码如下, 较之前的版本,此处加入了拟合时A,B,C参数的初始值设置(initialABC数组), 和A,B,C取值的范围(ABC_bounds数组).

代码在此

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import sys
import pylab as plb
# 拟合的函数设置为Antonnie方程 lgP=A-B/(C+T)
def func(T, A, B, C):
    return A - B / (C + T)

# 定义x、y散点坐标,T为绝对温度, lgP中P的单位为KPa再取对数.
data=plb.loadtxt("data.txt") #2列多行的数据, 第1列为T, 第2列为lgP.存为txt格式.
T = data[:,0]
lgP = data[:,1]
if len(T) != len(lgP):  # 检查x，y值是否尺寸一致。
    print("X轴与Y轴数据个数不一致"); sys.exit()
initialABC=[1,1,1] #设定A,B,C拟合时的初始值
ABC_bounds=([-np.inf, -np.inf, -250],[np.inf,np.inf,np.inf])#设定A,B,C的聚值范围,两个数据分别为A,B,C的下边界数组, 上边界数组.
popt, pcov = curve_fit(func, T, lgP, p0=initialABC, bounds=ABC_bounds)  #拟合过程在此函数中执行
A,B,C = popt
print('系数A, 参数B, 参数C');print('{0}\n{1}\n{2}'.format(A,B,C));
print('系数pcov:', pcov);
# 原始数据绘图
plot1 = plt.plot(T, lgP, 's', label='original data')
#拟合数据绘图
yvals = func(T, A, B, C)  # 拟合y值
print('根据拟合公式计算的结果:', yvals)
plot2 = plt.plot(T, yvals, 'r', label='fitting value')
plt.xlabel('T');plt.ylabel('lgP');plt.legend(loc=4);plt.title('lgP = {0} - {1}/({2}+T)'.format(A,B,C))
plt.show()

产生的结果如下:

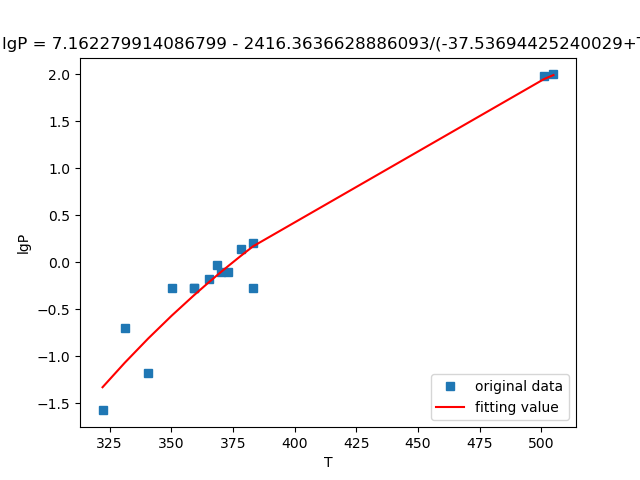
系数A, 参数B, 参数C
7.162279914086799
2416.3636628886093
-37.53694425240029

根据上述的结果, 可以得到TMSP的蒸气压回归方程为

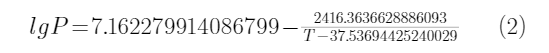
将温度298K代入上述方程(2)中, lgP=-2.109564, P即为7.7Pa. 即TMSP在25℃的蒸气压.

不过,有意思的是,我从Reaxys数据库也查到一组TMSP的沸点数据,它的拟合结果却不太合理, 有兴趣的朋友可以一起研究下.

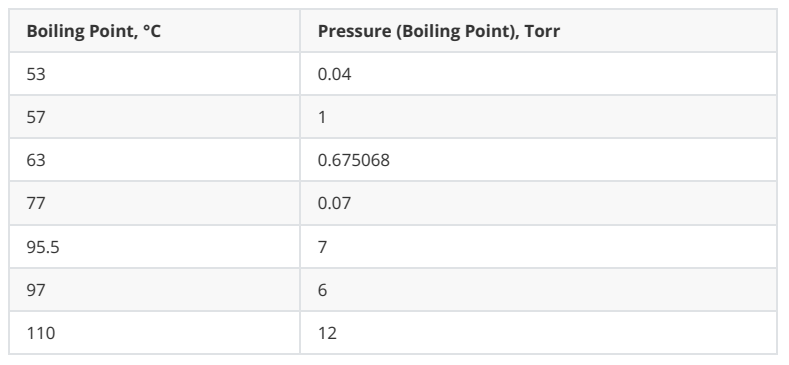
系数A: 0.26641985125269513
系数B: 14.815356637371815
系数C: -320.15321203726046 (这个拟合值有问题,导致温度低于320K时计算的蒸气压反而上升)