关于Kaczmarz方法和Randomized Kaczmarz方法

线性方程组

Kaczmarz的思想就是把大规模问题转化为一堆可分割的小问题，对应于现实就是每条行记录对应的数据都可以以非常低的代价单独处理。比如先看看下面这个线性方程组

\[Ax = b, \quad A \in \mathbb{R}^{m \times n} \]

这里先假定至少存在一个解，我们想要找到一个可行解。

---

那么怎么理解上面的线性方程组呢？一个直观解释就是m个n维空间中超平面的交集。设(a_i)是(A)的第(i)个行向量，那么

\[B_i = \{ x \mid a_i^T x = b_i \} \]

就是一个超平面，上面线性方程组等价于寻找集合的交集：

\[x \in \bigcap_{i = 1,2,\cdots,m} B_i \]

三维空间中的例子，下面这个欠定方程组就是两个二维平面的交集。

\[\begin{bmatrix} 1 & 1 & 1 \\ 1 & -1 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} \]

---

点到超平面的投影

有这么一类交替投影算法，大致是寻找N个集合Ci的交集，寻找一个点作为初始，然后轮流对各个集合做投影：\(x_{i + 1} = P_{C_{i\%N}}(x_i)\)
例子：

import numpy as np  

def project_on_circle(c, r, x): 
    if np.linalg.norm(x - c, 2) <= r:  
        return x  
    else:  =
        return (x - c) / np.linalg.norm(x - c) * r + c  
  
  
c = [np.array([2, 1]), np.array([2, -1])]  
r = [1.1, 1.1]  
  
x0 = np.array([0, 0])  
for it in range(10):  
    x1 = project_on_circle(c[it % 2], r[it % 2], x0)  
    x0 = x1  
print(x1)

---

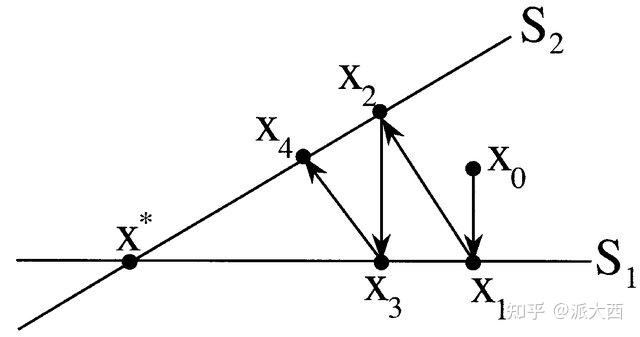
Kaczmarz迭代方法

复习一下(x)到平面\(B_i = \{ x \mid a_i^T x = b_i \}\)的投影：

\[x^* = P_{B_i}(x) = x + \frac{b_i - a_i^T x}{\| a_i \|^2} a_i \]

其中\(\frac{b_i - a_i^T x}{\| a_i \|^2}\)是点到线的距离，\(a_i\)为\(B_i\)的法向量。（做一个二维坐标轴不难发现）

---

那么对于线性方程组的话，就得到了如下的迭代算法：

\[x_{k + 1} = x_k + \frac{b_{i_k} - a_{i_k}^T x_k}{\| a_{i_k} \|^2} a_{i_k} \]

其中\(i_k = i \bmod m\). 实际上就是在超平面间轮流做投影。

---

Randomized Kaczmarz迭代方法

Randomized Kaczmarz 在原始 Kaczmarz 方法的基础上引入了随机性。在每次迭代时，不是按照固定顺序选择超平面，而是随机地选择一个超平面进行投影操作。指的是在选取\(i_k\) 时选取随机的超平面而不是循环取超平面。并且根据行范数大小选择迭代哪一个超平面。

\[x_{k + 1} = x_k + \frac{b_{i_k} - a_{i_k}^T x_k}{\| a_{i_k} \|^2} a_{i_k} \]

RK算法的收敛速度是指数阶的[1]。

RK算法改进

此外，RK算法进而延申出了非均匀抽取的随机Kaczmarz算法，即基于行范数概率准则进行加权概率抽样随机选取超平面。

然而当矩阵的所有行范数都相同，那么该方法所采用的行范数概率准则将等价于均匀抽样。就退化成了原始的RK算法，为此，引入了一种更有效的概率准则，构造了贪婪随机 Kaczmarz（Greedy Randomized Kaczmarz，或 GRK）方法。

目前有两个著名的贪婪准则：最大距离准则和最大残差准则。

最大距离准则

由于迭代中的投影是正交的，进而有

\[\|x_{k + 1} - x_*\|_2^2 = \|x_k - x_*\|_2^2 - \|x_{k + 1} - x_k\|_2^2 \]

因此，最优投影是使距离
\(\|x_{k + 1} - x_k\|_2^2\)
最大化的投影。

\[\|x_{k + 1} - x_k\|_2^2 = \left\|\frac{b^{(i)} - A^{(i)}x_k}{\|A^{(i)}\|_2^2}(A^{(i)})^T\right\|_2^2 \]

这说明在迭代过程中可以根据如下方式选择索引指标

\[t_k = \underset{i}{\arg\max}\left\|\frac{b^{(i)} - A^{(i)}x_k}{\|A^{(i)}\|_2^2}(A^{(i)})^T\right\|_2^2 = \underset{i}{\arg\max}\frac{(b^{(i)} - A^{(i)}x_k)^2}{\|A^{(i)}\|_2^2} \]

这个贪婪选择指标策略就是最大距离准则。

最大残差准则

而最大残差准则选择迭代指标主要根据

\[t_k = \underset{i}{\arg\max}(b^{(i)} - A^{(i)}x_k)^2 \]

也就是得到残差向量差值最大的指标。

参考

可以求解线性方程组的RK迭代
Kaczmarz算法原理
[1]A Randomized Kaczmarz Algorithm with Exponential Convergence
[2]Z. Z. Bai, W. T. Wu. On greedy randomized Kaczmarz method for solving large sparse linear systems [J]. SIAM J. Sci. Comput., 2018, 40 (1), A592-A606.
[3]张彦钧.数据科学中几类线性和非线性问题的随机方法研究