AR模型功率谱估计详解
一、核心原理
AR(自回归)模型功率谱估计是一种基于参数模型的现代谱估计方法,其核心思想是将信号建模为线性时不变系统的输出,通过估计系统参数(AR系数)推导功率谱。其数学模型为:
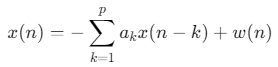
其中:
- \(p\)为模型阶数;
- \(a_k\)为AR系数;
- \(w(n)\)为白噪声(方差为\(σ_w^2\))。
功率谱密度(PSD)可表示为:
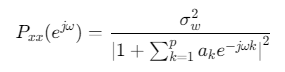
二、关键步骤
1. 模型参数估计
- Levinson-Durbin算法:通过递推求解Yule-Walker方程,适用于自相关法(
aryule/pyulear)。 - Burg算法:最小化前向与后向预测误差均方,避免矩阵求逆,适用于协方差法(
pburg)。 - 协方差法:直接优化前向预测误差(
pcov),适用于短数据。
2. 阶数选择
-
最终预测误差准则(FPE):
![]()
-
信息论准则(AIC):
![]()
选择使准则最小的p作为最佳阶数。
3. 功率谱计算
通过AR系数计算系统频率响应,进而得到功率谱。
三、MATLAB实现
1. 基本函数
| 函数 | 方法 | 输入参数 | 输出 |
|---|---|---|---|
pyulear |
自相关法 | x, p, NFFT, Fs |
Pxx, W |
pburg |
Burg算法 | x, p, NFFT, Fs |
Pxx |
pcov |
协方差法 | x, p, NFFT, Fs |
Pxx |
示例代码:
% 生成测试信号
Fs = 1000; n = 0:1/Fs:1-1/Fs;
xn = cos(2*pi*50*n) + cos(2*pi*120*n) + 0.5*randn(size(n));
% AR模型参数估计(阶数p=10)
p = 10;
[Pxx_pyulear, f_pyulear] = pyulear(xn, p, 1024, Fs);
[Pxx_pburg, f_pburg] = pburg(xn, p, 1024, Fs);
% 绘图对比
figure;
subplot(2,1,1);
plot(f_pyulear, 10*log10(Pxx_pyulear));
title('Levinson-Durbin (自相关法)');
subplot(2,1,2);
plot(f_pburg, 10*log10(Pxx_pburg));
title('Burg算法');
2. 阶数选择实现
% 计算不同阶数的预测误差
N = length(xn);
e_min = zeros(1, 50);
for p = 1:50
[a, e] = arburg(xn, p);
e_min(p) = e;
end
% AIC准则选择最佳阶数
aic = N*log(e_min) + 2*p;
[~, p_opt] = min(aic);
disp(['最佳阶数: ', num2str(p_opt)]);
四、应用场景
- 通信系统:调制信号载波频率估计(如AM/FM信号)。
- 生物医学:脑电信号(EEG)节律成分分析。
- 机械故障诊断:旋转机械振动信号中的故障频率检测。
- 地球物理:地震波频谱分析。
五、常见问题
- 虚假谱峰: 原因:阶数过高或噪声干扰。 解决:通过AIC/FPE准则选择合理阶数,增加正则化项。
- 分辨率不足: 原因:数据长度过短。 解决:采用多段平均(Welch方法)或增加采样率。
- 非平稳信号: 原因:AR模型假设信号平稳。 解决:分段处理或使用时频分析(如STFT)。
参考代码 AR模型功率谱估计 www.youwenfan.com/contentcnm/82014.html
总结
AR模型功率谱估计通过参数化建模实现高分辨率频谱分析,其核心在于模型阶数选择与算法优化。实际应用中需结合信号特性(如平稳性、噪声水平)选择合适方法,并通过预处理与后处理提升鲁棒性。


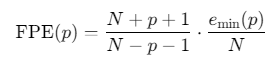
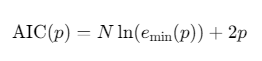

 浙公网安备 33010602011771号
浙公网安备 33010602011771号