斐波那契（矩阵实现）

大家都知道斐波那契数列，现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项。

斐波那契数列是一个满足 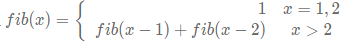的数列

数据范围：n<=39

这里只讲如何利用矩阵去计算
$$\left[\begin{array}{cccccccc}1& 0& & & & & & \\ 0& 1& & & & & & \\ 1& 1& 1& 0& & & & \\ 1& 2& 0& 1& & & & \\ 2& 3& 1& 1& 1& 0& & \\ 3& 5& 1& 2& 0& 1& & \\ 5& 8& 2& 3& 1& 1& 1& 0\\ 8& 13& 3& 5& 1& 2& 0& 1\end{array}\right]$$
我们不难看出这是一个分块矩阵

且我们可以得到以下规律
$$A=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$$

$$B=\left[\begin{array}{cc}1& 1\\ 1& 2\end{array}\right]$$

$$F(n)=B^n\ast A$$

其中n为输入的数除2再向上取整并减1

这里矩阵存储的是fib(1)、fib(2)…的个数。

代码实现：

# -*- coding:utf-8 -*-
class Solution:
    def Fibonacci(self, n):
        if n == 0:
            return 0
        a = [[1, 0], [0, 1]]
        b = [[1, 1], [1, 2]]
        f = 1
        m = n // 2 - 1
        if n % 2 != 0:
            m += 1
            f = 0
        for i in range(m):
            t = [[0, 0], [0, 0]]
            t[0][0] = b[0][0] * a[0][0] + b[0][1] * a[1][0]
            t[0][1] = b[0][0] * a[0][1] + b[0][1] * a[1][1]
            t[1][0] = b[1][0] * a[0][0] + b[1][1] * a[1][0]
            t[1][1] = b[1][0] * a[0][1] + b[1][1] * a[1][1]
            a = t
        return a[f][0]*1+a[f][1]*1

时间复杂度：O(log(n))

空间复杂度：O(1)