Leetcode题目解析
数组
1. 989-数组形式的整数加法
题目:
对于非负整数 X 而言,X 的数组形式是每位数字按从左到右的顺序形成的数组。例如,如果 X = 1231,那么其数组形式为 [1,2,3,1]。
| 示例: |
|---|
| 输入:A = [1,2,0,0], K = 34 |
| 输出:[1,2,3,4] |
| 解释:1200 + 34 = 1234 |
例程:
class Solution {
public:
vector<int> addToArrayForm(vector<int>& A, int K) {
vector<int> list;
for(int i = A.size()-1; i >= 0; i--){
int r = A[i] + K;
list.push_back(r % 10);
K = r / 10;
}
for(;K;K /= 10) list.push_back(K%10);
reverse(list.begin(),list.end());
return list;
}
};
解释:
-
K先与个位相加,与10取余后得到结果的个位数;
K整除10,舍弃个位,进行十位计算;
循环i次(即使过程中K为0,也不影响计算)
-
最后再附上K的单循环,防止K过大,为计算完。
2. 31-下一个队列
题目:
实现获取下一个队列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列。(即升序排列)
| 示例: |
|---|
| 输入:arr1 = [1,2,3] |
| 输出:[1,3,2] |
方法一:两遍扫描
程序:
C
void swap(int *a, int *b) { //互换函数(指针思想)
int t = *a;
*a = *b, *b = t;
}
void reverse(int *nums, int left, int right) { //区间倒序
while (left < right) {
swap(nums + left, nums + right);
left++, right--;
}
}
void nextPermutation(int *nums, int numsSize) {
int i = numsSize - 2; //指代倒数第二个数据
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--; //找到“较小数”
}
if (i >= 0) { //小于0则表示整个序列已经都是倒序状态
int j = numsSize - 1; //指代最后一个数据
while (j >= 0 && nums[i] >= nums[j]) {
j--; //找到“较大数”
}
swap(nums + i, nums + j); //先将“较小数”和“较大数”交换
}
reverse(nums, i + 1, numsSize - 1); //将“i+1”到最后一个数之间的区间进行倒序
}
C++
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int i = nums.size() - 2;
while (i >= 0 && nums[i] >= nums[i + 1]) {
i--;
}
if (i >= 0) {
int j = nums.size() - 1;
while (j >= 0 && nums[i] >= nums[j]) {
j--;
}
swap(nums[i], nums[j]);
}
reverse(nums.begin() + i + 1, nums.end());
}
};
解释:
- 先写好区间倒序函数reverse及其子函数swap(如果采用C++编程,则reverse和swap函数可直接调用);
- 该方法关键在于找到“较小数”和“较大数”,分别指:
- 较小数:从右向左轮询,找到第一对非倒序数对,则前者为需要替换的较小数;
- 较大数:从右向较小数轮询,找到第一个大于较小数的数,即为较大数;
- 将较小数和较大数交换;
- 将较小数后的数到最后一个数进行反转;
3. 1122-数组的排序
题目:
给定两个数组,arr1和arr2
- arr2中的元素各不相同
- arr2中的每个元素都出现在arr1中
对arr1中的元素进行排序,使arr1中项的相对顺序和arr2中的相对顺序相同。未在arr2中出现过的元素需要按照升序放在arr1的末端。
| 示例: |
|---|
| 输入:arr1 = [2,3,1,3,2,4,6,7,9,2,19], arr2 = [2,1,4,3,9,6] |
| 输出:[2,2,2,1,4,3,3,9,6,7,19] |
例程:
int* relativeSortArray(int* arr1, int arr1Size, int* arr2, int arr2Size, int* returnSize){
int nums[1001] = {0};
int *res = (int*)malloc(sizeof(int) * arr1Size);
int i;
int j = 0;
/* 统计数字出现的次数 */
for (i = 0; i < arr1Size; i++) {
nums[arr1[i]]++;
}
/* 先取出arr2中出现的数字 */
for (i = 0; i < arr2Size; i++) {
while (nums[arr2[i]] > 0) {
res[j++] = arr2[i];
nums[arr2[i]]--;
}
}
/* 将剩余数字升序排列 */
for (i = 0; i < 1001; i++) {
while (nums[i] != 0) {
res[j++] = i;
nums[i]--;
}
}
*returnSize = j;
return res;
}
C++
vector<int> SortArray(vector<int> arr1, vector<int> arr2) {
unordered_map<int,int> hashtable;
vector<int> res;
int j = 0;
for (int i = 0; i < arr1.size(); i++){
hashtable[arr1[i]]++;
}
for (int i = 0; i < arr2.size(); i++) {
while (hashtable[arr2[i]] > 0) {
res.push_back(arr2[i]); //这里必须用push_back
hashtable[arr2[i]]--;
}
}
for (int i = 0; i < 1001; i++) {
while (hashtable[i] != 0) {
res.push_back(i);
hashtable[i]--;
}
}
return res;
}
解释:
- 统计arr1中数字出现的次数(nums数组的值为arr1数值出现次数,nums数组编号才是arr1数值);
- 取出arr2中数组的数
- 将arr1中其他数值进行排序(nums数值顺序即为升序顺序!)
4. 88-合并两个有序数组
题目:
给定两个非递减顺序排列的整数数组nums1和nums2,另有两个整数m和n,分别表示nums1和nums2中的元素数组。
现需要合并nums2到nums1中,使合并后的数组同样非递减顺序排列。
| 示例: |
|---|
| 输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3 |
| 输出:[1,2,2,3,5,6] |
方法一:双指针法
例程:
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
vector<int> res;
int i = 0, j = 0;
while(i<m||j<n){ //类似合并两个有序链表
if(i==m){
res.push_back(nums2[j++]);
}else if(j==n){
res.push_back(nums1[i++]);
}else if(nums1[i]<nums2[j]){
res.push_back(nums1[i++]);
}else{
res.push_back(nums2[j++]);
}
}
nums1 = res;
return;
}
};
解释:
- 维护两个指针,直至指针指到数组结尾
- 思路类似合并两个有序链表
方法二:直接合并后排序
例程:
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
for (int i = 0; i != n; ++i) {
nums1[m + i] = nums2[i];
}
sort(nums1.begin(), nums1.end());
}
};
解释:
所有玩家都全力向前冲刺, 却不知道向后才是胜利之门。-《头号玩家》
链表
1. 21-合并两个有序链表
题目:
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
| 示例: |
|---|
| 输入:l1 = [1,2,4], l2 = [1,3,4] |
| 输出:[1,1,2,3,4,4] |

例程:
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if (l1 == nullptr) {
return l2;
} else if (l2 == nullptr) {
return l1;
} else if (l1->val < l2->val) {
l1->next = mergeTwoLists(l1->next, l2);
return l1;
} else {
l2->next = mergeTwoLists(l1, l2->next);
return l2;
}
}
};
解释:
- l1 = l1.next是指链表元素的指针,该句为指针的赋值;
- 思路
- 从各个链表的第一个元素开始比较,若l2>l1,则结果链表Curr指向l1,否则指向l2;
- 结果链表更新后,再将l1/l2链表指针后移一个;
- 结果链表指向最后一个元素时,因为已经跳出l1/l2不等于NULL的循环,所以进行选择赋值;
- 最后返回head.next(curr只是一个临时指针,最后要将指针指向第一个元素的head)
2. 24-两两交换链表中的节点
题目:
给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。(不是单纯改变链表内部的值,而是需要实际的进行节点交换。)
| 示例: |
|---|
| 输入:head = [1,2,3,4] |
| 输出:[2,1,4,3] |

例程:
struct ListNode* swapPairs(struct ListNode* head){
struct ListNode *p,*p1,*p2;
int n = 0;
p = head;
//确保链表不是全空
while (p != NULL){
//链表只有奇数元素时break
if(p->next == NULL)
break;
//元素二赋值给p1
p1 = p->next;
//如果是前两个元素,则p1为链表头
if(n == 0){
head = p1;
n = 1;
}
//否则p1为第三个元素
else
p2->next = p1;
//p p1 p2链表交换
p->next = p1->next;
p1->next = p;
p2 = p;
//p最终赋值为第三个元素
p = p->next;
}
return head;
}
解释:
- 首先确保链表不是全空
- 接着排除链表只有一个元素的情况
- 设置三个中间指针向量
- p赋初值head;
- p1赋初值p->next;
- 如果是第一次进判断,则p1赋值为head;
- 如果不是,p1赋值为p2->next;(上一循环的第二个元素)
- p1和p链表交换、p赋值给p2;
- p步进一个元素(下一组的第一个元素,一组两个元素)
3. 141-环形链表
题目:
给定一个链表,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪next指针再次到达,则链表中存在环。
为了表示给定链表中的环,我们使用整数pos来表示链表尾连接到链表中的位置(索引从0开始),如果pos是-1,则在该链表中没有环。(注:pos不作为参数进行传递,仅为了标识链表的实际情况)
如果链表中存在环,则返回true;否则,返回false。
| 示例: |
|---|
| 输入:head = [3,2,0,-4], pos = 1 |
| 输出:true |
| 解释:链表中有一个环,其尾部连接到第二个节点 |

例程:
bool hasCycle(struct ListNode *head) {
struct ListNode *fast,*slow;
fast = head;
slow = head;
while(fast != NULL && fast->next != NULL){
fast = fast->next->next;
slow = slow->next;
if(slow == fast)
return true;
}
return false;
}
解释:
上述程序应用了快慢链表的思想
fast链表每次步进两个元素
slow链表每次步进一个元素
有环的话fast链表会追上slow链表,进而两个链表元素相等,返回true;否则跳出循环,返回false。
还有程序应用hash set思想,还没看到。
4. 83-删除排序链表中的重复元素
题目:
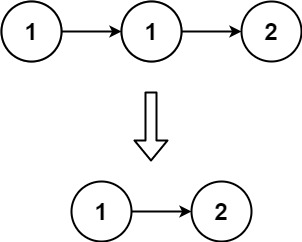
存在一个按升序排列的链表,给定链表头节点head,删除链表中的重复元素。
示例:
| 示例 |
|---|
| 输入:arr = [4,9,3], target = 10 |
| 输出:3 |
| 解释:当选择value为3时,数组变为[3,3,3],和为9,差值为1;当选择value为4时,数组变为[3,4,4],和为11,差值为1。但3比4小,所以输出3。 |
例程:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
if(!head)
return head;
ListNode *res = head; //记录头节点,最终要返回头节点
while(head){
int now_val = head->val;
if(head->next&&head->next->val == now_val){ //删除节点,防止内存泄漏
ListNode *del_Node = head->next;
head->next = head->next->next;
delete del_Node;
}
head = head->next;
}
return res;
}
};
解释:
- 两个问题,一个是判断元素是否相等,二是删除节点
- 判断元素相等,前提是head->next是有元素的,其次再判断值是否相等;
- 进而删除节点,删除节点时候三步走
- 新建节点,赋为中间节点
- head跳过中间节点
- 删除中间节点
5. 2-两数相加
题目:
给定两个非空链表,表示两个非负整数,每位数字按照逆序存储,每个节点只存储一位数字。请将两数相加,并以相同形式返回一个表示和的链表。
示例:
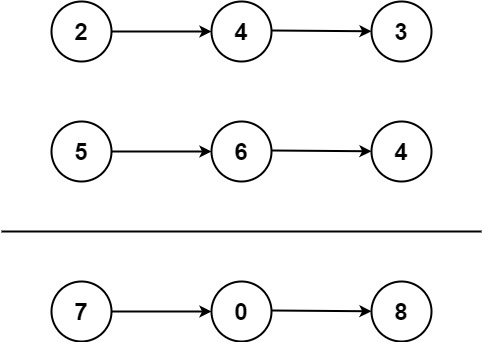
解释:342+465=807
例程:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode *head = nullptr,*tail = nullptr; //定义两个节点,一个为头节点,另一个用于维护
int tmp_val = 0;
while(l1||l2){ //主循环
int n1 = l1?l1->val:0;
int n2 = l2?l2->val:0;
int sum = n1+n2+tmp_val; //计算和
if(!head)
head = tail = new ListNode(sum%10); //定义头节点(新建节点的方式)
else{
tail->next = new ListNode(sum%10); //维护尾节点
tail = tail->next;
}
tmp_val = sum / 10; //保存进位
if(l1) //步进链表节点
l1 = l1->next;
if(l2)
l2 = l2->next;
}
if(tmp_val) //计算结束仍有进位,继续新建节点
tail->next = new ListNode(tmp_val);
return head;
}
};
解释:
- 关键在于要新建两个节点,一个记录头地址,一个用来维护;
- 每个节点通过new的形式新建
- 不要忘记最后的进位有可能单独成为一个节点。
6. 61-旋转链表
题目:
给定一个链表头节点head,旋转链表,将链表每个节点向后移动k个位置
示例:
| 示例: |
|---|
| 输入:head = [1,2,3,4,5],k = 2 |
| 输出:[4,5,1,2,3] |
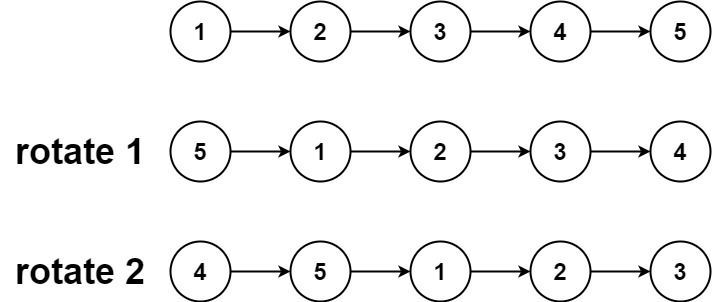
方法一:双指针法
例程:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
ListNode* slow, *fast, *res, *pTemp;
slow = head;
fast = head;
res = head;
pTemp = head;
int count = 0;
if(head == nullptr) //排除空指针
return pTemp;
while(pTemp!=nullptr){ //获取链表长度
pTemp=pTemp->next;
count++;
}
if(k>count) //更新k
k = k%count;
else if(k == count)
return res;
while(k--){ //获取前指针
fast = fast->next;
}
while(fast->next!=nullptr){ //遍历链表
slow = slow->next;
fast = fast->next;
}
fast->next = res; //修改链表结构
res = slow->next;
slow->next = nullptr;
return res;
}
};
解释:
- 维护两个指针,一个慢指针,从链表头开始遍历;另一个快指针,从头+k处开始遍历;
- 定位后,修改链表结构即可。
方法二:闭合成环
例程:
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if (k == 0 || head == nullptr || head->next == nullptr) {
return head;
}
int n = 1;
ListNode* iter = head;
while (iter->next != nullptr) {
iter = iter->next;
n++; //确定链表长度
}
int add = n - k % n;
if (add == n) {
return head;
}
iter->next = head;
while (add--) {
iter = iter->next; //确定尾节点
}
ListNode* ret = iter->next;
iter->next = nullptr;
return ret;
}
};
解释:
- 先将链表连接成环
- 再在指定位置断开
7. 206-反转链表
题目:
给定一个单链表的头节点head,请你反转链表,并返回反转后的链表。
示例:
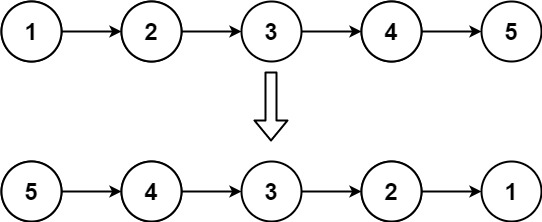
| 示例: |
|---|
| 输入:head = [1,2,3,4,5] |
| 输出:[5,4,3,2,1] |
方法一:迭代
例程:
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr; //保存前一个节点
ListNode* curr = head;
while (curr) {
ListNode* next = curr->next; //获取下一个节点
curr->next = prev; //改变指针指向
prev = curr; //更新前节点
curr = next; //更新现指针
}
return prev;
}
};
解释:
- 遍历链表,将当前节点next指向前一个节点;
- 所以需要保存前一个节点,但同时需要更新指针,所以也要保存下一个节点
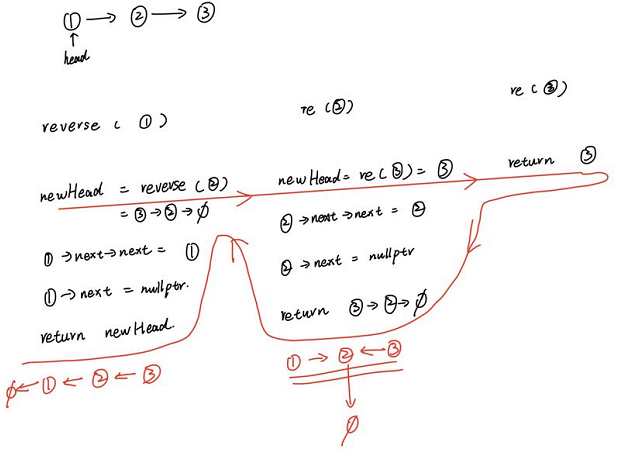
方法二:递归
例程:
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if (!head || !head->next) {
return head;
}
ListNode* newHead = reverseList(head->next);
head->next->next = head;
head->next = nullptr;
return newHead;
}
};
解释:
- head->next->next = head,指head节点的下一个节点指向head
- 同时要保证尾节点必须指向nullptr,否则会产生环
树
1. 572-另一个树的子树
题目:
给定两个非空二叉树s和t,检验s中是否包含和t具有相同结构和节点值的子树。s的一个子树包括s的一个节点的所有子孙。s也可以看做它自身的一颗子树。
示例1:
给定的树s

给定的树t

返回True
示例2:
给定的树s

给定的树t

返回False
方法一:深度优先搜索(Depth First Search,DFS)
例程
class Solution {
public:
//基本的树检测函数
bool check(TreeNode *s, TreeNode *t) {
if (!s && !t) {
return true;
}
if ((s && !t) || (!s && t) || (s->val != t->val)) {
return false;
}
return check(s->left, t->left) && check(s->right, t->right);
}
//DFS逻辑函数
bool dfs(TreeNode *s, TreeNode *t) {
if (!s) {
return false;
}
return check(s, t) || dfs(s->left, t) || dfs(s->right, t);
}
//调用DFS
bool isSubtree(TreeNode *s, TreeNode *t) {
return dfs(s, t);
}
};
解释
使用DFS枚举s中的每一个子节点,判断这个点的子树和t是否相等。
方式是让两个指针一开始先指向该节点和t的根,然后同步移动两根指针来同步遍历这两颗树。
方法二:深度优先搜索序列上做串匹配
方法三:树哈希
2. 297-二叉树的序列化和反序列化
题目:
请设计一个算法来实现二叉树的序列化和反序列化。(不限序列化和反序列化的执行逻辑,只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构)
| 示例: |
|---|
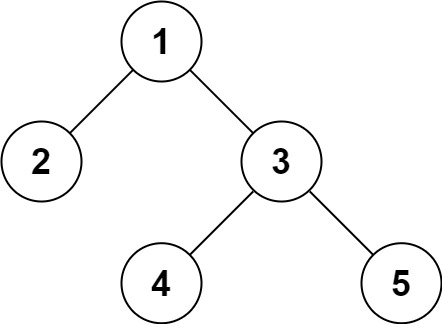
| 输入:root = [1,2,NULL,NULL,3,4,NULL,NULL,5,NULL,NULL] |
| 输出:[1,2,NULL,NULL,3,4,NULL,NULL,5,NULL,NULL] |
程序:
class Codec {
public:
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
if(root == NULL)
return "NULL,"; //检测到空树,返回NULL
string res = to_string(root->val) + ","; //不是空节点,则将元素转为字符串类型,并加上该节点元素
res += serialize(root->left); //左孩子递归
res += serialize(root->right); //左孩子递归结束,自下而上继续右孩子递归
return res;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
std::stringstream ss(data); //队列相关可参考https://www.cnblogs.com/john1015/p/12956593.html
std::string item;
queue<string> q;
while (std::getline(ss, item, ',')) //常用分隔","方式
q.push(item); //至此得到完整的队列q(包含所有树数据)
return helper(q);
}
TreeNode* helper(queue<string>& q) //还原二叉树
{
string val = q.front(); //获取队列最前端元素
q.pop(); //获取后即弹出该元素
if (val == "NULL")
return NULL;
TreeNode* head = new TreeNode(stoi(val)); //stoi()为带范围检查的string转int的函数 参考https://blog.csdn.net/qq_33221533/article/details/82119031 atoi才是char转int
head->left = helper(q);
head->right = helper(q);
return head;
}
};
解释:
- DFS
- 检测空节点,返回NULL;
- 否则执行计算(to_string(val)+“,”);
- 递归左孩子;
- 递归右孩子。
- 队列
- getline(),用于分割符号“,”,push用于将分割出的元素推入队列(先进先出);
- q.front() 获取队列最前端元素,接着pop(),即弹出该元素;
- 接着使用DFS的思想进行还原二叉树:
- 如果val为“NULL”,则return NULL;
- 否则,对二叉树指针内容进行正常赋值(使用stoi(val),将字符串类型转为int)
- 递归左孩子;
- 递归右孩子。
3. 129-求根节点到叶节点数字之和
题目:
给一个二叉树的根节点root,树中每个节点都存放有一个0-9之间的数字,每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径为1->2->3,表示数字123。
计算从根节点到叶节点生成的所有数字之和。
(叶节点是指没有子节点的节点)
| 示例: |
|---|
| 输入:root = [1,2,3] |
| 输出:25 |
| 解释:12+13 |

例程:
int dfs(struct TreeNode* root, int prevSum) {
if (root == NULL) { //空节点,则返回0
return 0;
}
int sum = prevSum * 10 + root->val; //只要不是空节点,就累加
if (root->left == NULL && root->right == NULL) {
return sum; //表明已经到达叶节点
} else {
return dfs(root->left, sum) + dfs(root->right, sum); //否则继续搜索
}
}
int sumNumbers(struct TreeNode* root) {
return dfs(root, 0);
}
解释:
深度优先搜索,带参数的累加(将过去累加值作为参数)
- dfs,首先判断是否为空节点,是则返回;否则经过计算,再进行递归(return原函数)
- 将之前的累加值设置为dfs的参数,方便处理累加值。
哈希
1. 1-两数之和
题目:
给定一个整数数组nums和一个整数目标值target,请在该数组中找出“和为目标值”的那两个整数,并返回它们的数组下标。(假定每种输入只会对应一个答案,但是数组中同一元素在答案里不能重复出现。)
| 示例: |
|---|
| 输入:nums= [2,7,11,15], target = 9 |
| 输出:[0,1] |
| 解释:nums[0]+nums[1]=9 |
程序:
1.暴力枚举法
int* twoSum(int* nums, int numsSize, int target, int* returnSize){
for(int i = 0;i < numsSize-1;i++){
for (int j = i+1;j<numsSize;j++){
if (nums[i]+nums[j]==target){
int* res = malloc(sizeof(int) * 2);
res[0] = i;
res[1] = j;
*returnSize = 2;
return res;
}
}
}
*returnSize = 0;
return NULL;
}
解释:
- 第一个for循环确定第一个数;
- 第二个for循环确定第二个数,且该数是从第一个数后面开始遍历;
- 二者相加和为target则返回结果,否则返回NULL。
2. 哈希表
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> hashtable;
for (int i = 0; i < nums.size(); ++i) {
auto it = hashtable.find(target - nums[i]);
if (it != hashtable.end()) {
return {it->second, i};
}
hashtable[nums[i]] = i;//先找后加入表,防止查到自己(元素5,target=10)
}
return {};
}
};
解释:
- 构建哈希表(unordered_map类型,第一个参数为键(索引)、第二个参数为值);
- 进入唯一的for循环;
- 查找哈希表中有无(target-nums[i]),有则返回对应矩阵;
- find(val) 查找以 val 为键的键值对,如果找到,则返回一个指向该键值对的正向迭代器(it->first为键,it-second为值);反之,则返回一个指向容器中最后一个键值对之后位置的迭代器,即 尾后迭代器(end())
- 否则将将该元素值赋值给哈希表的键、序列号赋值给值;
- 如果一个for循环跑完了还没有,就return空。
2. 451-根据字符出现频率排序
题目:
给定一个字符串,请将字符串里的字符按照出现的频率降序排列
| 示例: |
|---|
| 输入:"tree" |
| 输出:"eert"or"eetr" |
| 解释:'e'出现两次,排在前面;'t'和'r'谁先谁后无所谓 |
例程:
class Solution {
public:
string frequencySort(string s) {
unordered_map<char, int> mp;
int maxFreq = 0;
int length = s.size();
for (auto &ch : s) {
maxFreq = max(maxFreq, ++mp[ch]); //获取存放字符与数量的哈希表
}
vector<string> buckets(maxFreq + 1); //获取最大数量+1长度的数组,用于存放所有字符,注意是vector<string>
for (auto &[ch, num] : mp) {
buckets[num].push_back(ch); //获取存放所有字符的数组,数组位置即字符数量
}
string ret;
for (int i = maxFreq; i > 0; i--) {
for (auto &ch : buckets[i]) { //bucket[i]存放同样数量的元素,依次打印这些字符
for (int k = 0; k < i; k++) {
ret.push_back(ch);
}
}
}
return ret;
}
};
解释:
- 先构建哈希表,依次存放字符与字符出现次数;
- 再将哈希表转换为数组,数组字符元素的编号即为出现次数;
- 依次打印出这些字符
栈
1. 394-字符串解码
题目:
给定一个经过编码的字符串,返回它解码的字符串。
编码规则为:k[string],k表示string重复了k次,k为正整数。
| 示例: |
|---|
| 输入:s = "3[a]2[bc]" |
| 输出:"aaabcbc" |
| 解释:3次a+2次bc |
方法一:子函数+递归
程序
class Solution {
public:
pair<string,int> solver(const string&s, int i){
int multiplier = 0;
string mul = "";
string ans = "";
while(i < s.length()){
if(s[i] >= '0'&&s[i] <= '9'){ //检测到是数字,则将数字累加(字符串形式)
mul = mul + s[i];//这里没有把之前的数据位清除
//multiplier = multiplier*10 +s[i] - '0'; //这里通过直接将字符串解算成int
}else if (s[i] == '['){ //检测到左括号,进行递归,再检测,再递归,直至检测到']'
auto sub_ans = solver(s,i+1);
i = sub_ans.second;
multiplier = stoi(mul); //字符串类型转为int
while(multiplier > 0){
ans += sub_ans.first; //字符串重复
multiplier--;
}
mul = ""; //清空mul
}else if (s[i] == ']'){ //检测到']',返回数据对
return pair(ans,i);
}else { //检测到字母,则字符串ans++
ans += s[i];
}
i++; //进行下一次检测
}
return pair(ans,i); //返回总的数据对
}
string decodeString(string s) {
return solver(s,0).first;
}
};
解释:
- 子函数solver,若i<字符串s长度,则:
- 检测到数字,则字符串累加
- 检测到'[',进行递归,直至检测到']'
- 递归
- stoi(mul),将字符串转为int
- 基于multiplier,进行字符串ans重复
- 检测到']',返回当前数据对pair
- 否则即检测到字母,进行字符串ans++
- i++,进行下一次检测
- i>字符串s长度,检测结束,返回最终pair数据对
方法二:栈操作
程序:
class Solution {
public:
string getDigits(string &s, size_t &ptr) { //获取数字子函数
string ret = "";
while (isdigit(s[ptr])) { //此处while循环是为了获取二位数及以上的倍数
ret.push_back(s[ptr++]); //此处已经将ptr++
}
return ret;
}
string getString(vector <string> &v) { //为了将string数组v中的字符串全部导出为单独的字符串
string ret;
for (const auto &s: v) {
ret += s;
}
return ret;
}
string decodeString(string s) {
vector <string> stk;
size_t ptr = 0;
while (ptr < s.size()) {
char cur = s[ptr];
if (isdigit(cur)) {
// 获取一个数字并进栈
string digits = getDigits(s, ptr); //该函数内已经将ptr++
stk.push_back(digits);
} else if (isalpha(cur) || cur == '[') {
// 获取一个字母并进栈
stk.push_back(string(1, s[ptr++]));
} else { //检测到右括号,开始出栈
++ptr;
vector <string> sub; //子字符串数组
while (stk.back() != "[") {
sub.push_back(stk.back());
stk.pop_back();
}
reverse(sub.begin(), sub.end());
// 左括号出栈
stk.pop_back();
// 此时栈顶为当前 sub 对应的字符串应该出现的次数
int repTime = stoi(stk.back());
stk.pop_back();
string t, o = getString(sub);
// 构造字符串
while (repTime--) t += o;
// 将构造好的字符串入栈
stk.push_back(t);
}
}
return getString(stk);
}
};
解释:
-
主循环
- 判断元素是否为数字,是则入栈;
- 判断元素是否为字符/'[',是则获取一个元素入栈;
- 否则元素即为']',开始出栈
- 重新定义子字符串数组;
- 自右向左依次将原栈最后一个元素入栈到新数组,紧接着出栈,依次循环,直至检测到'[';
- 将栈内元素倒置,获得正序元素;
- 或者栈顶元素,即为倍数,并stoi转化为int类型
- 构建字符串,并将其入栈
- 返回第一步
-
子函数
-
getdigits,获取倍数
isdigit(char),判断char是否为数字
-
getstring,将字符串类型数组转为字符串
isalpha(char),判断char是否为字符串
-
2. 739-每日温度
题目:
根据每日气温列表,重新生成一个列表,对应位置的数据为“想要观测到更高的气温,至少需要等待的天数”
如果该日气温后续不再上升,则对应位置数据置0
| 示例: |
|---|
| 输入:temperatures = [73,74,75,71,69,72] |
| 输出:[1,1,0,2,1,0] |
方法:单调栈
程序:
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
int n = T.size();
vector<int> ans(n);
stack<int> s;
for (int i = 0; i < n; ++i) {
while (!s.empty() && T[i] > T[s.top()]) { //栈非空,且当前数据大于栈顶数据
int previousIndex = s.top();
ans[previousIndex] = i - previousIndex;
s.pop();
}
s.push(i);
}
return ans;
}
};
解释:
- 遍历数组内元素,且维护一个单调栈
- 若栈非空,且当前元素值大于栈顶元素值,则计算天数差,并保存在结果数组ans中,同时弹出参与比较的元素;
- 否则将数组元素压入栈内,即为新的栈顶元素(栈为空或者当前元素小于栈顶元素的情况)
- 返回结果数组ans
堆
1. 295-数据流的中位数
题目:
中位数是有序列表中间的数,如果列表长度是偶数,中位数是中间两个数的平均值。
设计一个支持以下两种操作的数据结构:
- void addNum(int num) - 从数据流中添加一个整数到数据结构中;
- double findMedian() - 返回目前所有元素的中位数
| 示例: |
|---|
| 输入:addNum(1) addNum(2) findMedian() addNum(3) findMedian() |
| 输出:[null, null, null, 1.5, null, 2.0] |
方法一:暴力法
程序:
class MedianFinder {
vector<double> store;
public:
// Adds a number into the data structure.
void addNum(int num)
{
store.push_back(num); //数组中加入元素
}
// Returns the median of current data stream
double findMedian()
{
sort(store.begin(), store.end()); //将数组中数据按从小到大的顺序放置
int n = store.size();
return (n & 1 ? store[n / 2] : (store[n / 2 - 1] + store[n / 2]) * 0.5); //返回中位数
}
};
解释:
- 设置存储数组store;
- addNum函数用push_back指令将数据压入数组中;
- 用sort函数将store数组中的元素按从小到大排列,并返回中位数。
但这样写会超时!!!
n&1指的是n的最低位与1想与,若为奇数,则返回1;若为偶数,则返回0.
方法二:插入排序
程序:
class MedianFinder {
vector<int> store; // resize-able container
public:
// Adds a number into the data structure.
void addNum(int num)
{
if (store.empty()) //空矩阵则直接将数据存入
store.push_back(num);
else //否则通过insert插入,insert的键值由lower_bound获取
store.insert(lower_bound(store.begin(), store.end(), num), num); // binary search and insertion combined
}
// Returns the median of current data stream
double findMedian()
{
int n = store.size(); //接下来直接同暴力法相同
return n & 1 ? store[n / 2] : (store[n / 2 - 1] + store[n / 2]) * 0.5;
}
};
解释:
中心思想与暴力法一致,先获取排序好的数组store,然后再return中位数
-
AddNum函数:
-
如果Store为空,则直接将数据压入矩阵;
-
否则通过insert插入数据,insert的键由lower_bound函数获取
lower_bound(First,Last,num)指搜索(First,Last)之间第一个不小于num的数的键;
insert(key,num)指在key处插入num
-
-
findMedian()同暴力法,直接返回中位数
方法三:大顶堆和小顶堆(优先级队列)
程序:
class MedianFinder {
priority_queue<int> lo; // max heap
priority_queue<int, vector<int>, greater<int>> hi; // min heap
public:
// Adds a number into the data structure.
void addNum(int num)
{
lo.push(num); // Add to max heap
hi.push(lo.top()); // balancing step
lo.pop();
if (lo.size() < hi.size()) { // maintain size property
lo.push(hi.top());
hi.pop();
}
}
// Returns the median of current data stream
double findMedian()
{
return lo.size() > hi.size() ? (double) lo.top() : (lo.top() + hi.top()) * 0.5;
}
};
解释:
通过构建并平衡两个大顶堆和小顶堆,来获取最中间的数字(一个/两个);
-
定义一个大顶堆和一个小顶堆,即“priority_queue”格式
优先队列(priority_queue)用法:
- top 访问对头元素
- empty 队列是否为空
- size 返回队列内元素个数
- push 插入元素到队尾(并排序)
- emplace 原地构造一个元素并插入队列
- pop 弹出队头元素
- swap 交换内容
定义格式:
priority_queue<int, vector
, greater >指小顶堆 priority_queue<int, vector
, less >指大顶堆(默认) -
AddNum函数
- 大顶堆压入一个数据,并将大顶堆顶端数据压入小顶堆,并弹出;
- 检测大顶堆数据是否大于等于,否则将小顶堆顶端数据压入大顶堆,并弹出;
以上两步可以保证二者相互平衡或接近。
-
findMedian函数
判断大顶堆和小顶堆数据是否相等,来确定是单数数据还是双数,并return对应中位数。
双指针及二分
1. 15-三数之和
题目:
给一个包含n个整数的数组nums,判断nums中是否存在三个元素a,b,c,使得a+b+c=0?
请找出所有和为0且不重复的三元组。
| 示例1: |
|---|
| 输入:nums = [-1,0,1,2,-1,-4] |
| 输出:[[-1,-1,2],[-1,0,1]] |
| 示例2: |
|---|
| 输入:nums = [] |
| 输出:[] |
方法:排序+双指针
程序
class Solution {
public:
vector<vector<int>> twoSum(vector<int>& nums, int start, int end, int target, int value){
vector<vector<int>> answer;
while(start < end){
int sum = nums[start] + nums[end];
if(sum == target){ //找到目标和
vector<int>result; //定义结果子数组
result.push_back(value); //第一个数组元素
result.push_back(nums[start]); //第二个数组元素
result.push_back(nums[end]); //第三个数组元素
answer.push_back(result); //压入结果数组
while(start < end && nums[start] == nums[start+1]){ //防止重复,移动指针
start++;
}
start++; //继续搜索下一组
while(start < end && nums[end] == nums[end-1]){ //防止重复,移动指针
end--;
}
end--; //继续搜索下一组
}else if(sum < target){
start++; //如果和小于目标值,则后移前向指针
}else{
end--; //如果和大于目标值,则前移后向指针
}
}
return answer; //返回结果数组(仅对应一个解的数组)
}
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> answer; //好家伙,原来是这样定义的
sort(nums.begin(), nums.end()); //方便执行双指针,对数组进行排序
int size = nums.size();
for(int i = 0;i < size;i++){
if(i>0&&nums[i] == nums[i-1]){
continue; //如果两个数组元素相等,则跳过,不再执行twoSum
}
auto result = twoSum(nums,i+1,size-1,-nums[i],nums[i]); //result即为子函数的answer
answer.insert(answer.end(),result.begin(),result.end()); //在anwer.end处插入数组
}
return answer;
}
};
解释:
-
将数组元素排序,依次遍历一遍,将三数之和问题转变为两数之和问题;
排序的目的是为了方便执行双指针算法,从两侧依次逼近target;
-
twoSum函数
-
定义结果子数组:vector<vector
> answer,数组中的元素还为数组时,这样定义; -
第一个指针start指向输入元素的后一个元素,第二个指针end,即剩余元素的最小值和最大值,sum等于二者之和;
-
当sum大于target值时,end指针前移;当sum小于target值时,start指针后移;
-
当sum等于target时,先将当前元素包装起来(即先赋值到一个临时数组中),再将包装后的元素赋值到answer数组中;
同时start指针后移,end指针前移,继续搜索有无其他成立的数组元素。
-
-
threeSum函数
- 定义结果数组,通上面定义结果子数组一样;
- 利用sort函数将数组元素排序,方便执行双指针操作;
- 开始遍历数组元素,如果遇到元素相同的,则直接跳过(利用if判断和continue语句实现),遍历过程中执行twoSum子函数,并将输出结果插入到answer.end(),即尾后迭代器的位置。
- 返回整个结果数组answer。
2. 350-两个数组的交集II
题目:
给定两个数组,编写一个函数来计算它们的交集。
(输出元素出现的次数等于两个数组元素出现次数的最小值)
| 示例1: |
|---|
| 输入:nums1 = [1,2,2,1], nums2 = [2,2] |
| 输出:[2,2] |
| 示例2: |
|---|
| 输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4] |
| 输出:[4,9] |
(将每个元素视为独立个体,即检测独立个体的出现次数)
方法一:哈希表
程序:
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
if (nums1.size() > nums2.size()) { //始终确保nums1为较短的数组
return intersect(nums2, nums1);
}
unordered_map <int, int> m;
for (int num : nums1) {
++m[num]; //构建哈希表
}
vector<int> intersection;
for (int num : nums2) { //遍历nums2数组
if (m.count(num)) { //返回哈希表m中含有“num”键的数量
intersection.push_back(num); //向结果数组中压入num
--m[num]; //num数量减一
if (m[num] == 0) { //num数量为0时,哈希表m删除该元素
m.erase(num);
}
}
}
return intersection; //返回结果数组
}
};
解释:
- 构建哈希表,将nums1元素存入哈希表,值为nums1元素数量,键为nums1元素值;(归根到底还是一种排序的方式)
- 遍历数组nums2
- 如果哈希表中存在nums2元素,则将该元素压入结果数组;
- 并将哈希表该元素的值-1;
- 若该元素值为0,则删除哈希表该元素。
- 返回结果数组。
方法二:排序+双指针
程序:
class Solution {
public:
vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
sort(nums1.begin(), nums1.end());
sort(nums2.begin(), nums2.end()); //将数组1和数组2进行排序
int length1 = nums1.size(), length2 = nums2.size();
vector<int> intersection;
int index1 = 0, index2 = 0;
while (index1 < length1 && index2 < length2) { //当指针均未超出数组长度
if (nums1[index1] < nums2[index2]) {
index1++; //数组1元素小于数组2,则数组1指针后移
} else if (nums1[index1] > nums2[index2]) {
index2++; //数组1元素大于数组2,则数组2指针后移
} else { //数组1和数组2元素相等时
intersection.push_back(nums1[index1]); //数据压入结果数组
index1++;
index2++; //两个指针同时后移
}
}
return intersection;
}
};
解释:
- 先将两个数组进行排序(sort函数);
- 当两个指针均未超出数组长度时:
- 若数组1元素小于数组2,则数组1指针后移;
- 若数组1元素大于数组2,则数组2指针后移;
- 若二者元素相等,则将此时元素数值压入结果数组(push_back函数),并将两个指针同时后移
- 返回结果数组
3. 1300-转变数组后最进阶目标值的数组和
题目:
给定一个整数数组arr和一个目标值target,请返回一个整数value,使得将数组中所有大于value的变成value后,数组的和最接近target(最接近表示两者之差的绝对值最小)
如果有多种使得和最接近target的方案,请返回这些整数中的最小值。
答案不一定是arr中的数字。
| 示例1: |
|---|
| 输入:arr = [4,9,3], target = 10 |
| 输出:3 |
| 解释:当选择value为3时,数组变为[3,3,3],和为9,差值为1;当选择value为4时,数组变为[3,4,4],和为11,差值为1。但3比4小,所以输出3。 |
方法:二分查找
程序:
class Solution {
public:
int Sum_Vector(vector<int> arr, int res) { //计算数组和
int ret = 0;
for (auto num : arr)
ret += num >= res ? res : num;
return ret;
}
int findBestValue(vector<int>& arr, int target) {
sort(arr.begin(),arr.end());
int n = arr.size();
vector<int> presum(n + 1);
for (int i = 1; i <= n; i++) //获取前缀和
presum[i] = presum[i-1] + arr[i - 1];
int value;
int min = 0, max = *max_element(arr.begin(), arr.end()); //二分查找的范围,即val的范围
while (min <= max) {
int mid = (min + max) / 2;
auto iter = lower_bound(arr.begin(), arr.end(), mid); //返回不小于mid的第一个值的正向迭代器
int cur = presum[iter - arr.begin()] + (arr.end() - iter)*mid; //计算当前数组和
if (cur <= target) {
value = mid;
min = mid + 1;
}
else
max = mid - 1;
}
return (abs(Sum_Vector(arr, value) - target) <= abs(Sum_Vector(arr, value + 1) - target) ? value : value + 1);
}
};
解释:
- 对于给定数组,首先先将其进行排序;
- 接着通过遍历数组中元素,获取整个数组对应的前缀和数组;
- 根据题意,确定value的取值范围为[0, max(arr)],程序里设置为[min,max]
- 设置while循环,通过二分法查找到满足条件“数组和小于target”的最大数组和对应的value;
- 二分法的过程是,若数组和小于target,则提高下限min;否则降低上限max。
- 因为增大value值,对应的数组和是严格单调递增的,所以最终的value一定是上述步骤求出的value和value+1之中的一个,所以只需要对比二者的数组和大小即可得到结果。
滑动窗口
1. 209-长度最小的子数组
题目:
给定一个含有n个正整数的数组和一个正整数target。
找出该数组中满足其和>=target的长度最小的连续子数组[nums1, nums2, ..., numsr],并返回其长度。
如果不存在符合条件的子数组,返回0.
| 示例1: |
|---|
| 输入:arr = [2,3,1,2,4,3], target = 7 |
| 输出:2 |
| 解释:子数组[4, 3]是该条件下的长度最小的子数组。 |
| 示例2: |
|---|
| 输入:arr = [1,4,4], target = 4 |
| 输出:1 |
方法一:前缀和+二分查找
程序:
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int n = nums.size();
int res = INT_MAX; //先令结果为最大值
vector<int> preSum(n + 1, 0);
for (int i = 1; i <= n; i++) { //获取前缀和数组
preSum[i] = preSum[i - 1] + nums[i-1];
}
for (int i = 1; i <= n; i++) {
int tmp = target + preSum[i - 1]; //因为数组全是正数,搜索target+前缀和的low_bound,相当于仅搜索当前结点的target的low_bound
auto bound = lower_bound(preSum.begin(), preSum.end(), tmp);
if (bound != preSum.end())
res = min(res, static_cast<int>((bound - preSum.begin()) - (i - 1)));
}
return ((res == INT_MAX) ? 0 : res);
}
};
解释:
-
求取前缀和preSum数组;
-
遍历数组元素,通过二分法(调用函数low_bound)返回最小的不小于target的元素迭代器;
因为数组元素均为正,所以数组和是单调递增的。
即low_bound函数调用的是前缀和+target
-
通过min函数不断进行比较前一步res和该步计算出的数组长度。
方法二:滑窗
程序:
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int n = nums.size();
if (n == 0) {
return 0;
}
int ans = INT_MAX;
int start = 0, end = 0; //即双指针
int sum = 0;
while (end < n) {
sum += nums[end]; //更新sum
while (sum >= s) { //sum>=target
ans = min(ans, end - start + 1); //比较res
sum -= nums[start]; //减去第一项继续比较
start++; //首指针后移
}
end++; //末指针后移
}
return ans == INT_MAX ? 0 : ans;
}
};
解释:
- 设置两个指针(实际上就是两个int类型的索引值)start和end;
- 当end<数组长度时,进while循环,更新sum值
- 当sum大于target时,进while循环,获取当前长度,并比较较小值;
- 减去start元素值,并后移start;
- 若sum仍大于target,继续上述两个步骤,否则出while循环。
- end后移
- 最终返回res
2. 3-无重复字符的最长子串
字符串
1. 844-比较含退格的字符串
题目:
给定S和T两个字符串,当它们分别被输入到空白的文本编辑器后,判断二者是否相等,并返回结果。
代表退格字符。
注意:如果对空文本输入退格字符,文本继续为空。
| 示例1: |
|---|
| 输入:S = "ab#c", T = "ad#c" |
| 输出:true |
| 解释:S和T都会变成"ac"。 |
| 示例1: |
|---|
| 输入:S = "a#c", T="b" |
| 输出:false |
| 解释:S会变成"c",但T仍然是"b"。 |
方法一:string find函数
程序:
class Solution {
public:
string set(string str){
while(str.find('#')!=-1){ //若数组中没有find到,则返回npos,即-1
auto pos = str.find('#');
str.erase(pos,1); //删除'#'
if(pos!=0)
str.erase(pos-1,1); //如果'#'不是在第一个,则删除前一个元素
}
return str;
}
bool backspaceCompare(string s, string t) {
return(set(s)==set(t));
}
};
解释:
- 如果没有find到,则返回原字符串;否则进循环
- 删除'#'
- 若'#'前有元素,则删除该元素
方法二:维护栈
程序:
class Solution {
public:
bool backspaceCompare(string S, string T) {
return build(S) == build(T);
}
string build(string str) {
string ret;
for (char ch : str) {
if (ch != '#') {
ret.push_back(ch);
} else if (!ret.empty()) {
ret.pop_back();
}
}
return ret;
}
};
解释:
- 遍历数组所有元素,如果不是'#',则存入string(push_back)
- 否则,若string不为空,则删除一个元素(pop_back)
方法三:双指针
程序:
class Solution {
public:
bool backspaceCompare(string S, string T) {
int i = S.length() - 1, j = T.length() - 1;
int skipS = 0, skipT = 0;
while (i >= 0 || j >= 0) {
while (i >= 0) {
if (S[i] == '#') {
skipS++, i--;
} else if (skipS > 0) {
skipS--, i--;
} else {
break; //既不是指向'#',skipS也不大于0,则跳出循环
}
}
while (j >= 0) {
if (T[j] == '#') {
skipT++, j--;
} else if (skipT > 0) {
skipT--, j--;
} else {
break; //既不是指向'#',skipT也不大于0,则跳出循环
}
}
if (i >= 0 && j >= 0) {
if (S[i] != T[j]) {
return false;
}
} else {
if (i >= 0 || j >= 0) {
return false;
}
}
i--, j--;
}
return true;
}
};
解释:
通过维护两个指针,每次比较两个指针元素指向的数值相不相等即可。
2. 796-旋转字符串
题目:
给定两个字符串,A和B
A的旋转操作就是将A最左边的字符移动到最右边。例如A=“abcde”,移动一次之后结果就是“bcdea”。
如果若干次旋转操作之后,A能变成B,那么返回True。
| 示例1: |
|---|
| 输入:A = "abcde", B = "cdeab" |
| 输出:true |
| 示例2: |
|---|
| 输入:A = "abcde", B = "abced" |
| 输出:false |
方法一:暴力穷举法
程序:
class Solution {
public:
bool rotateString(string A, string B) {
if(A.empty()&&B.empty()) //均为空,则返回True
return true;
if((A.empty()&&!B.empty())||(!A.empty()&&B.empty())||(A.size()!=B.size()))
return false; //一方为空,一方不为空或者二者长度不等,则返回False
for(int i = 0; i < A.size(); i++){
A += A[0];
A.erase(0,1); //构建新字符串A
if(A==B) //字符串A与目标字符串B比较,相同则返回True
return true;
}
return false;
}
};
解释:
- 先排除一些特殊情况
- 以字符串A长度为循环次数,构建A的所有移动情况,再与B比较,相等则返回True。
方法二:判断子串
程序:
class Solution {
public boolean rotateString(String A, String B) {
return A.length() == B.length() && (A + A).contains(B);
}
}
解释:
由于A+A包含了所有通过“旋转”操作得到的字符串,所以只需要判断B是否为A+A的子串即可。
方法三:KMP算法
上述两种算法的时间复杂度均为O(N^2),用KMP算法的时间复杂度为O(N),后面复习到动态规划再看。
3. 151-翻转字符串里的单词
题目:
给定一个字符串s,逐个翻转字符串中的所有单词。
单词是由非空格字符组成的字符串。s中使用至少一个空格将字符串中的单词分隔开。
请你返回一个翻转s中单词顺序并用单个空格相连的字符串。
| 示例1: |
|---|
| 输入:s = "the sky is blue" |
| 输出:"blue is sky the" |
| 示例2: |
|---|
| 输入:s = " hello world " |
| 输出:"world hello" |
方法三:暴力法数组法
程序:
class Solution {
public:
string reverseWords(string s) {
string tmp, res;
vector<string> demo;
for (int i = 0; i < s.length(); i++) {
if (s[i] != ' ') {
tmp += s[i]; //确定单个元素
}
else if (s[i] == ' ' && !tmp.empty()) {
demo.push_back(tmp); //将单个元素压入数组
tmp = ""; //清空临时字符串
}
if (i == s.length() - 1 && !tmp.empty()) {
demo.push_back(tmp);
tmp = "";
}
}
for (int j = demo.size() - 1; j > 0; j--) {
res += demo[j] + ' '; //依次将数组中的元素抽出来(倒序)
}
res += demo[0]; //最后一位直接加上
return res;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号