树
非空树中只有一个根结点,根结点无直接前驱;一棵树又可以划分为多棵树
-
结点的度:一个结点拥有的子树的个数称为此结点的度
树的度: 树中所有的结点的度的最大值
-
叶子结点或终端结点: 度为0的结点——即无后继的结点
分支结点或非终端结点:度不为0的结点
孩子结点:一个结点的直接后继称为该结点的孩子结点
双亲结点:一个结点的直接前驱称为该结点的双亲结点
兄弟结点:同一双亲结点的孩子结点之间互称兄弟结点
祖先结点:一个结点的祖先结点是指从根结点到该结点的路径上所经历的所有结点
子孙结点: 一个结点的直接后继和间接后继
-
结点的层次:定义从根结点开始起,根结点的层次为1,根的直接后继的层次为2,依此类推
树的深度或高度:树中所有的结点的层次的最大值
任何一棵树是一个二元组 Tree = (root,F),其中:root是树的根结点,F 称为子树森林
6.2 二叉树
二叉树的特点
-
二叉树由3个基本单元组成: 根结点、左子树和右子树。二叉树中,每个结点至多有二棵子树
-
二叉树的子树有左、右之分,其次序不能颠倒
-
二叉树的结构最简单,规律性最强
-
可以证明,所有的树都能转为唯一对应的二叉树
-
满二叉树和完全二叉树
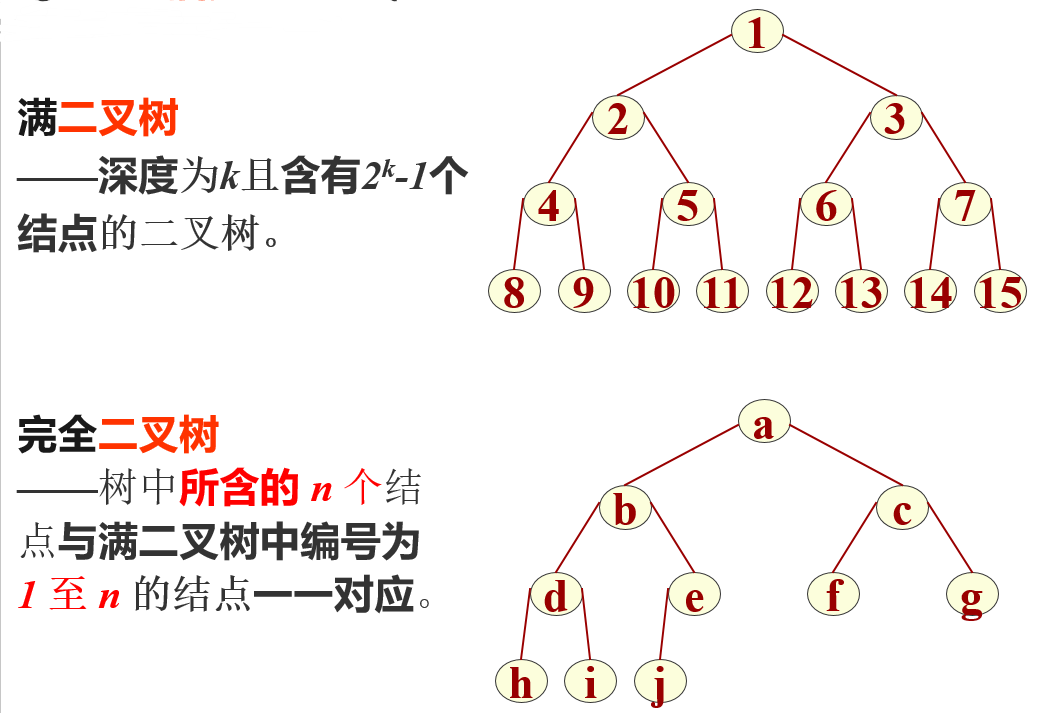
6.2.1 性质
-
在二叉树的第 i 层上至多有2^\left(i-1\right) 个结点 ( i≥1 )
-
深度为 k 的二叉树至多含 2^k-1 个结点(k≥1)
-
对任何一棵二叉树,若它含有n_0 个叶子结点(度为0)、n_2 个度为2 的结点,则必存在关系式:n_0 = n_2+1
证明:设 二叉树结点总数为n,则 n = n_0 + n_1 + n_2,其中n_1为度为1的结点数,又因为二叉树上的分支总数为: n-1 =n_1+2n_2, 可得到: n_0 = n_2 + 1
-
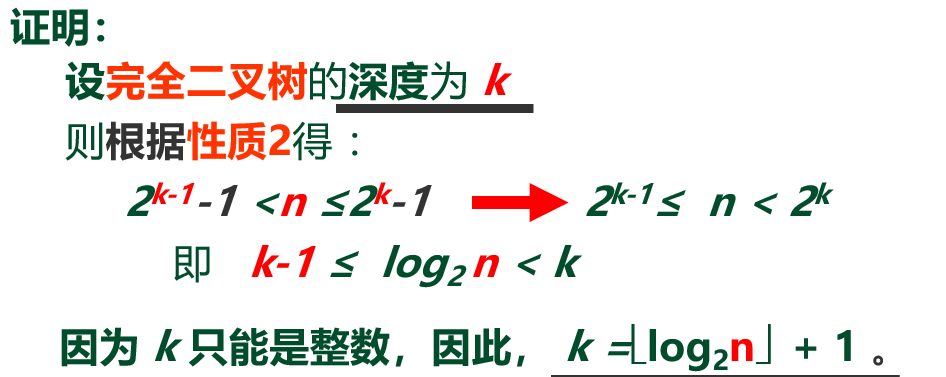
具有 n 个结点的完全二叉树的深度 k = \left \lfloor log_2n \right \rfloor +1
![]()
-
若对含 n 个结点的完全二叉树从上到下且从左至右进行 1 至 n 的编号,则对完全二叉树中编号为 i 的结点:
-
若 i=1,则该结点是二叉树的根,无双亲,
否则,编号为 \left \lfloor i/2\right \rfloor的结点为其双亲结点;
-
若 2i>n,则该结点无左孩子结点,
否则,编号为 2i 的结点为其左孩子结点;
-
若 2i+1>n,则该结点无右孩子结点
否则,编号为2i+1 的结点为其右孩子结点
-
6.2.2 顺序存储结构
用一组地址连续的存储单元(一维数组)依次自上而下、自左至右存储完全二叉树上的结点元素——将完全二叉树上编号为i的结点元素存储在一维数组中下标为i-1的数组分量中
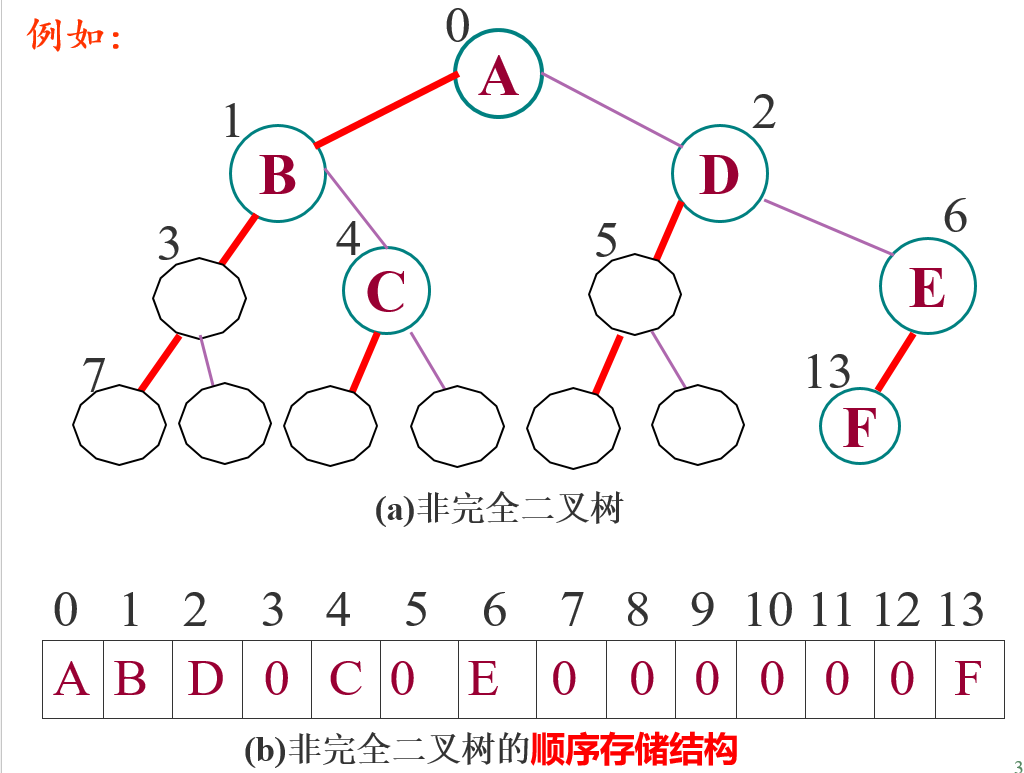
缺点
-
单支二叉树就是一个极端的浪费很多存储空间的情况。因此,这种方式仅仅适合于满二叉树和完全二叉树
-
若经常需要插入和删除树中结点时,顺序存储方式也不是很好
6.2.3 链式存储
结点的结构

1 typedef struct BiTNode { 2 TelemType data; 3 struct BiTNode *lchild,*rchild; //存左右孩子的指针 4 } BiTNode, *BiTree; //结点类型 BiTNode
6.2.4 遍历算法
递归遍历
L、D、R分别表示遍历左子树、访问根结点和遍历右子树,并限定遍历操作是先左后右
-
先(根)序遍历(DLR)
-
中(根)序遍历 (LDR)
-
后(根)序遍历 (LRD)
1 // 先(根)序遍历(DLR) 2 void PreOrderTraverse(BiTree T, Status (*Visit)( TElemType )) 3 {// 初始条件: 二叉树T存在, Visit是对结点数据操作的应用函数。 4 // 操作结果: 先序遍历二叉树T, 对每个结点调用一次Visit函数。 5 if ( T ) //T非空 6 { Visit( T->data );//访问根结点 7 PreOrderTraverse(T->lchild, Visit);//先序遍历左子树 8 PreOrderTraverse(T->rchild, Visit);//先序遍历右子树 9 } 10 }
1 // 最简单的Visit函数: 2 Status Visit(TElemType e) 3 { printf( e );//输出元素e的值, 实用时要加上格式串 4 return OK; 5 }
三种算法均未对空子树作标记,不能由其中一种唯一确定一棵树,解决方法:
-
对空子树作标记,得到的遍历序列就称为“扩展的遍历序列”
-
先序和中序序列 或 中序和后序序列 两者一起确定
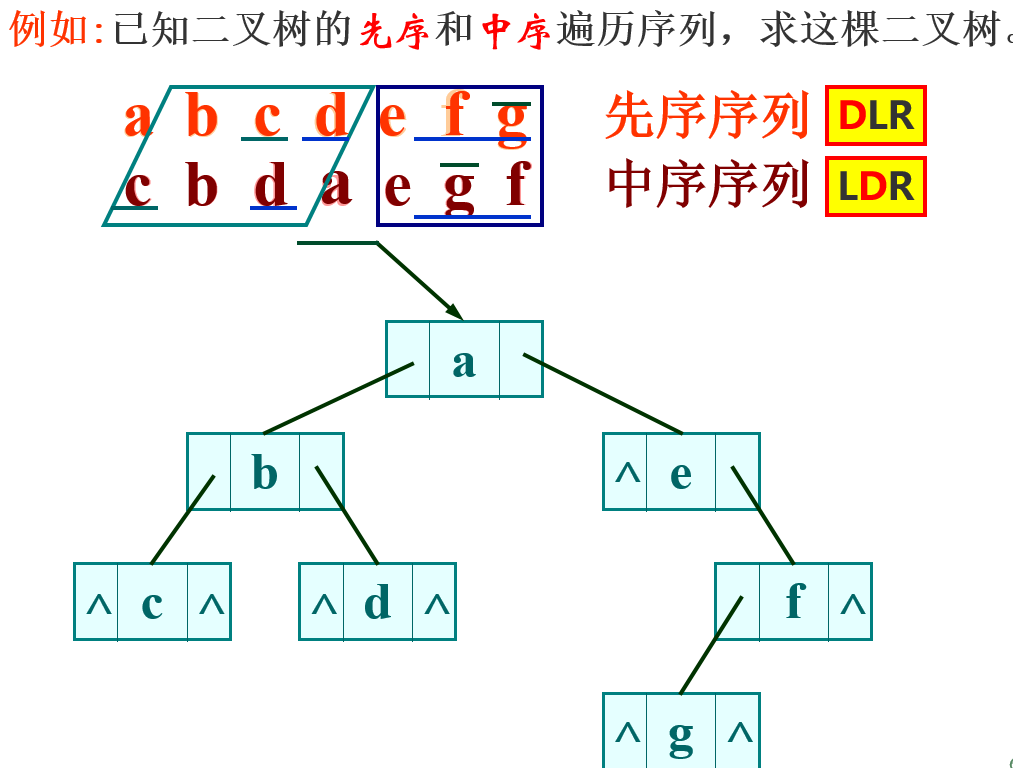
恢复二叉树的核心是 : 寻找根结点
层次遍历
若树不空,则从上到下,从左到右, 依次访问树中每个结点
应用举例
统计二叉树的叶子结点
1 void CountLeaf(BiTree T, int &count ) 2 { if ( T ) 3 { if ((!T->lchild)&& (!T->rchild)) count++; 4 // 对叶子结点计数 5 CountLeaf( T->lchild, count); 6 CountLeaf( T->rchild, count); 7 } 8 }
求二叉树的深度
1 int Depth( BiTree T ) // 返回二叉树的深度 2 { if ( !T ) depthval = 0; 3 else { depthLeft = Depth( T->lchild ); 4 depthRight= Depth( T->rchild ); 5 depthval = (depthLeft > depthRight ? depthLeft : depthRight) +1; 6 } 7 return depthval; 8 }
复制二叉树
1 BiTNode *GetTreeNode(TElemType item, BiTNode *lptr, BiTNode *rptr ) 2 { //生成一个二叉树的结点 3 //其数据域为item, 左指针域为lptr, 右指针域为rptr 4 if (!( T = (BiTNode*)malloc( sizeof(BiTNode) ) ) ) exit(1); 5 T-> data = item; T-> lchild = lptr; T-> rchild = rptr; 6 return T; 7 } 8 9 BiTree CopyTree( BiTree T ) 10 {if ( !T ) return NULL; 11 if (T->lchild) newlptr = CopyTree(T->lchild);//复制左子树 12 else newlptr = NULL; 13 if (T->rchild)newrptr = CopyTree(T->rchild);//复制右子树 14 else newrptr = NULL; 15 newT=GetTreeNode( T->data, newlptr, newrptr ); 16 //生成结点 17 return newT; 18 }
6.2.5 线索二叉树
含n个结点的二叉链表中含有 (n+1)个空指针域,可以利用这些空指针域存放结点在某种遍历操作下结点的前趋或后继结点的指针

类型定义
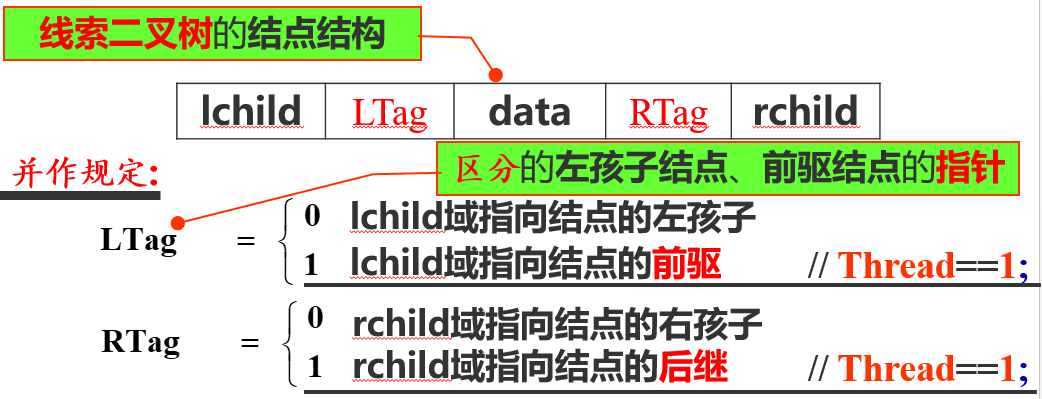
为了为了便于写代码: (1)在线索链表上增加一个头结点,并令头结点的lchild指针指向线索二叉树的根结点,令头结点的rchild指针指向中序遍历时访问的最后一个结点 (2)令线索二叉树的中序遍历序列中的第一个结点的lchild指针和最后一个结点的rchild指针均指向头结点
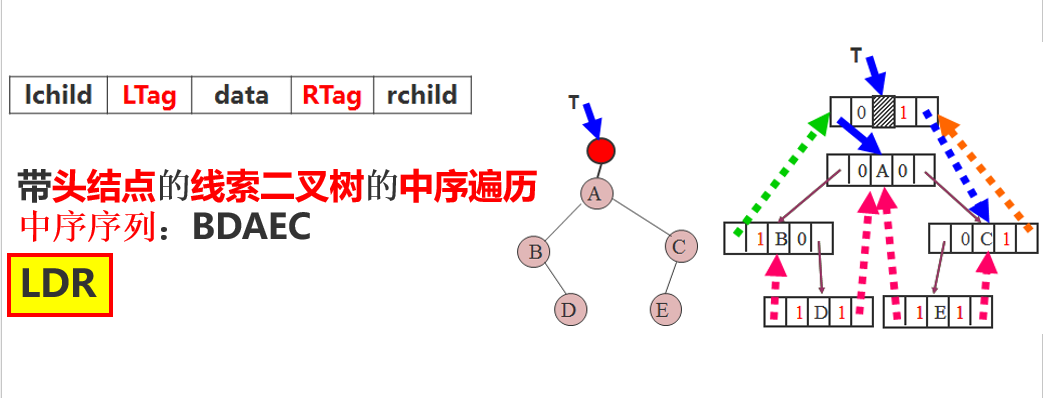
1 typedef enum { Link, Thread } PointerTag ;// Link==0; Thread==1; 2 typedef struct BiThrNode{ 3 TElemType data; 4 struct BiThrNode *lchild, *rchild; 5 PointerTag LTag, RTag; // 左、右标志 6 } BiThrNode, *BiThrTree;
二叉树的中序递归遍历线索化
1 Status InOrderThreading( BiThrTree &Thrt, BiThrTree T ) 2 { //中序遍历二叉树T,并将其中序线索化,Thrt指向头结点 3 if (!(Thrt = (BiThrTree)malloc( sizeof(BiThrNode) ) ) ) 4 exit (OVERFLOW); //创建头结点 5 Thrt->LTag = Link; Thrt->RTag = Link; 6 Thrt->rchild = Thrt;//头结点的右指针回指 7 if (!T) Thrt->lchild=Thrt; //若是空树, 则头结点的左指针也回指 8 else { Thrt->lchild = T; pre = Thrt; 9 10 InThreading( T );//中序遍历进行中序线索化 11 12 pre->rchild = Thrt;//最后一个结点右部线索化 13 pre->RTag = Thread; 14 Thrt->rchild = pre; 15 } 16 return OK; 17 } 18 19 void InThreading(BiThrTree p) 20 { 21 if (p) // 对以p为根的非空二叉树进行中序线索化 22 { 23 InThreading(p->lchild); //左子树线索化 24 if (!p->lchild) { p->Ltag =Thread;p->lchild=pre;} 25 //若 结点p的左子树为空, 则建立该结点p的前驱线索 p->lchild=pre 26 if (!pre->rchild) { pre->Rtag = Thread;pre->rchild=p; 27 //若 前驱pre的右子树为空, 则建立该pre结点的后继线索 pre->rchild=p 28 } 29 30 pre = p; //p结点已访问,用pre代指,是下一个要访问结点的前驱 31 InThreading(p->rchild); //右子树线索化 32 } 33 }
带头结点的中序线索链表T中序遍历算法
1 Status InOrderTraverse_Thr( BiThrTree T, 2 Status(*Visit)( TElemType ) ) 3 { // T 指向头结点,头结点的lchild指向根结点 4 // 对每个数据元素调用函数Visit 5 p=T–>lchild;// p 指向根结点 6 while (p!=T)// 遍历结束时, p==T 7 { 8 while (p –>LTag ==Link) p=p –>lchild;//找最左下结点 9 if ( !Visit(p –>data) ) return ERROR;//访问最左下结点 10 while ( p –>RTag ==Thread && p –>rchild!=T ) 11 { p=p –>rchild; Visit(p –>data); }//情况(1)该结点无右子树;直接访问后继结点 12 13 p= p–>rchild; //情况(2)该结点有右子树;则从其右子树重新开始 14 } 15 return OK; 16 }
核心:寻找最左下的结点,访问后继结点(rchild)
6.3 树和森林
6.3.1 3种树的存储结构
双亲表示法
以一组地址连续的存储单元存储树的所有结点, 在每个结点中设一个指示器指示其双亲结点在表中的位置
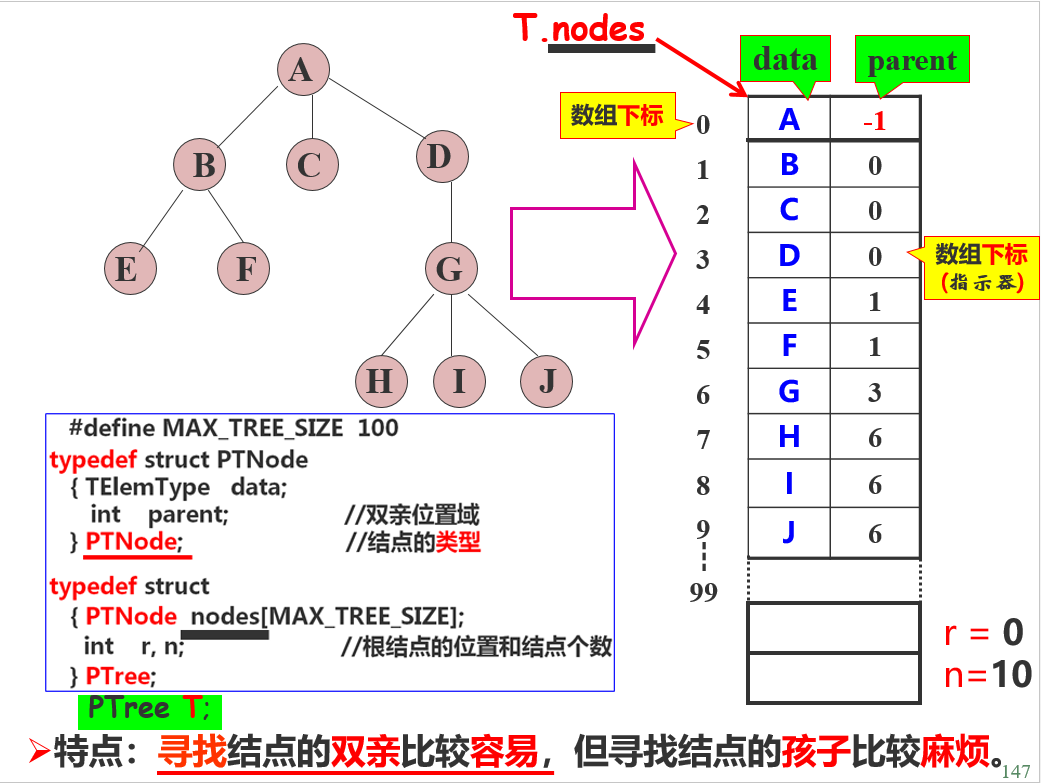
孩子表示法
把每一个结点的孩子结点排列起来, 构成一个单链表。n个结点有n个孩子链表(叶子结点的孩子链表为空表)。并将n个结点的数据和n个孩子链表的头指针组成一个顺序表
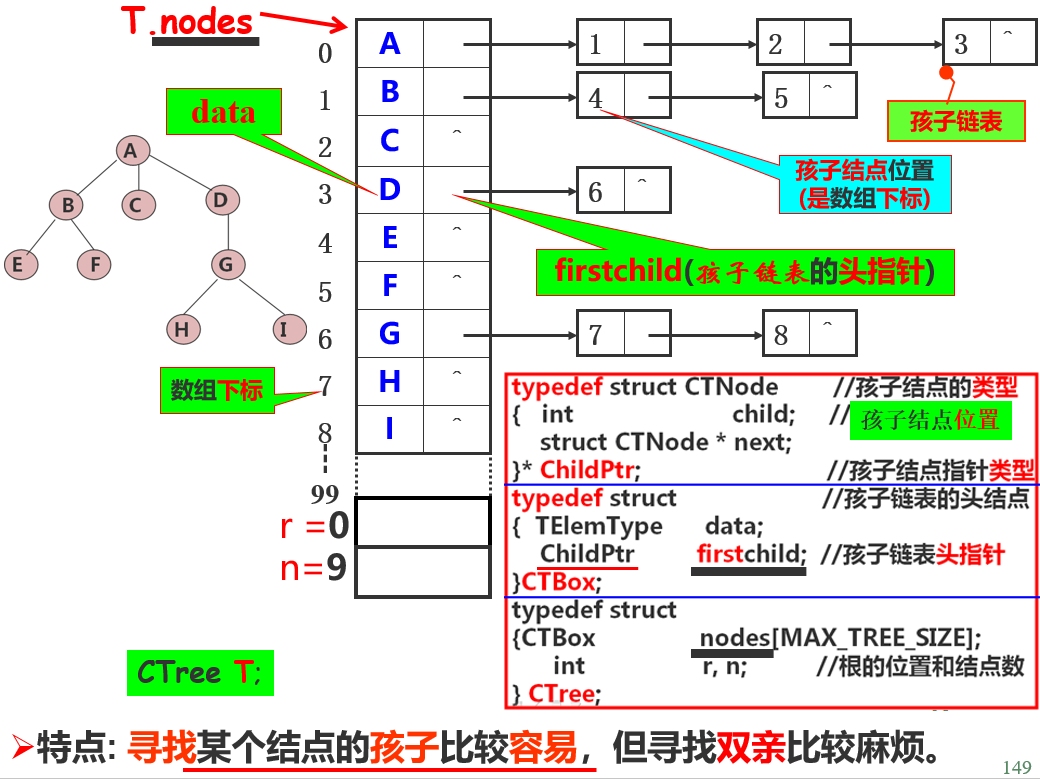
带双亲的孩子表示法
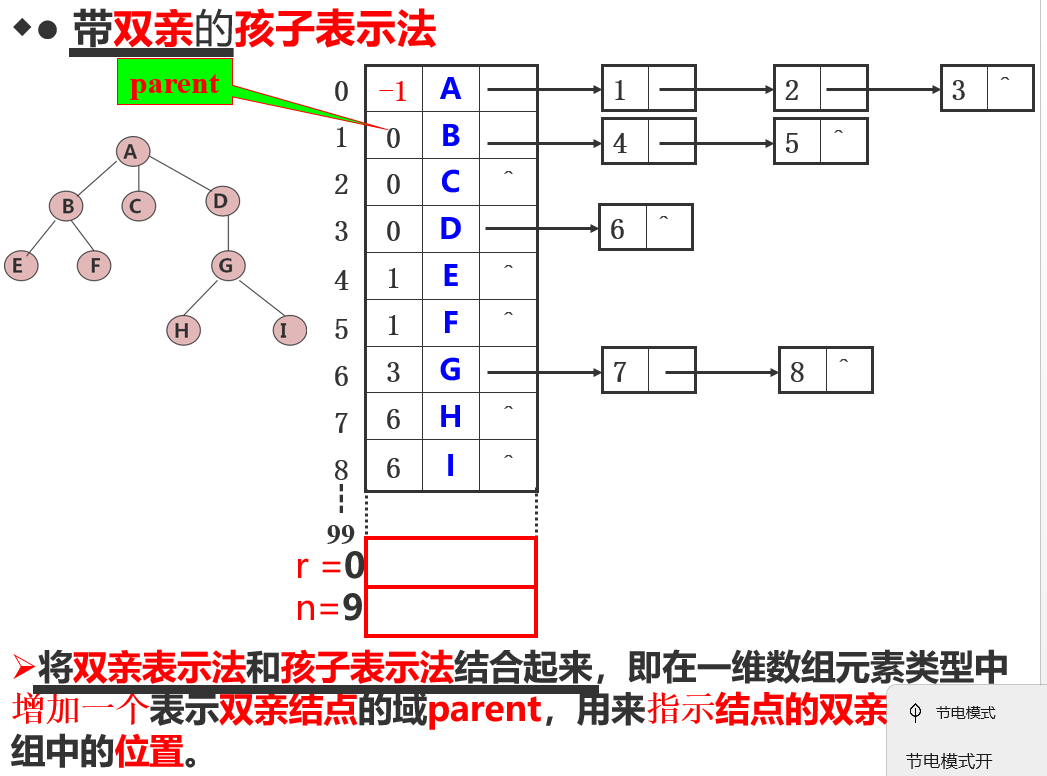
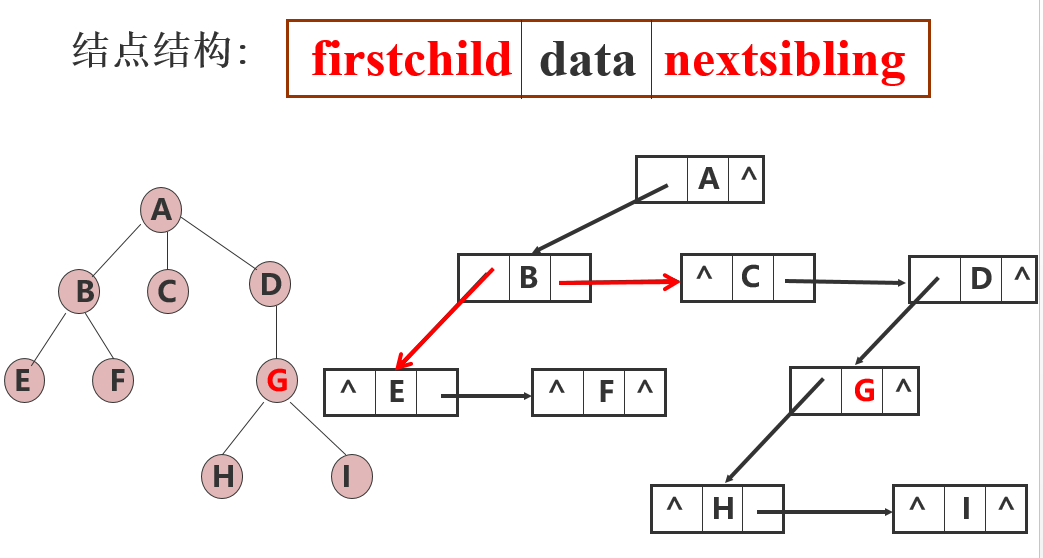
孩子兄弟表示法
该方法仍然采用二叉链表作为树的存储结构,但是二叉链表中结点的两个指针域分别指向该结点的第一个孩子结点和指向该结点的右边第一个兄弟结点
6.3.2 森林和二叉树的转换
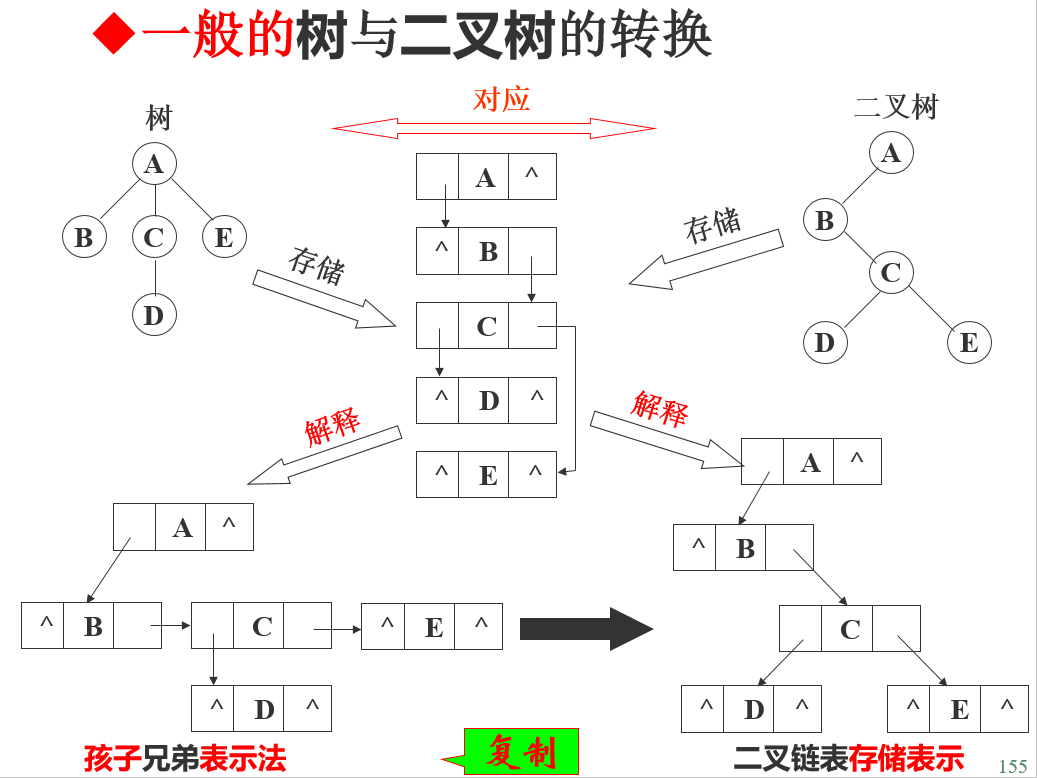
一般树转换为二叉树
可以先将这棵树用孩子兄弟表示法存储, 此时, 树中的每个结点有两个指针: 一个指针指向第一个孩子, 另一个指针指向右侧第一个兄弟,当把其两个指针看作是二叉树中的左孩子指针和右孩子指针时, 就是一棵二叉树
森林的遍历
6.3.3 赫夫曼树
在用 n 个叶子结点构造一棵二叉树时,必存在一棵二叉树的带权路径长度WPL最小的二叉树,称为最优二叉树或赫夫曼树
-
路径:从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。
路径长度:路径上的分支的数目称作路径长度。
-
结点的路径长度:从根结点到该结点的路径上经历的分支的数目。
结点的带权路径长度:从树根到该结点之间的路径长度与该结点的权值的乘积。
-
树的路径长度: 从树根到树中每一个结点的路径长度之和。
树的带权路径长度: 树中所有叶子结点的带权路径长度之和
WPL = \sum_{k=1}^{n} w_k l_k
其中: n 为树中叶子结点的总个数, w_k 为第 k 个叶子结点的权值, l_k 为第k 个叶子结点的路径长度,wk \times lk 为第k个叶子结点的带权路径长度
赫夫曼算法
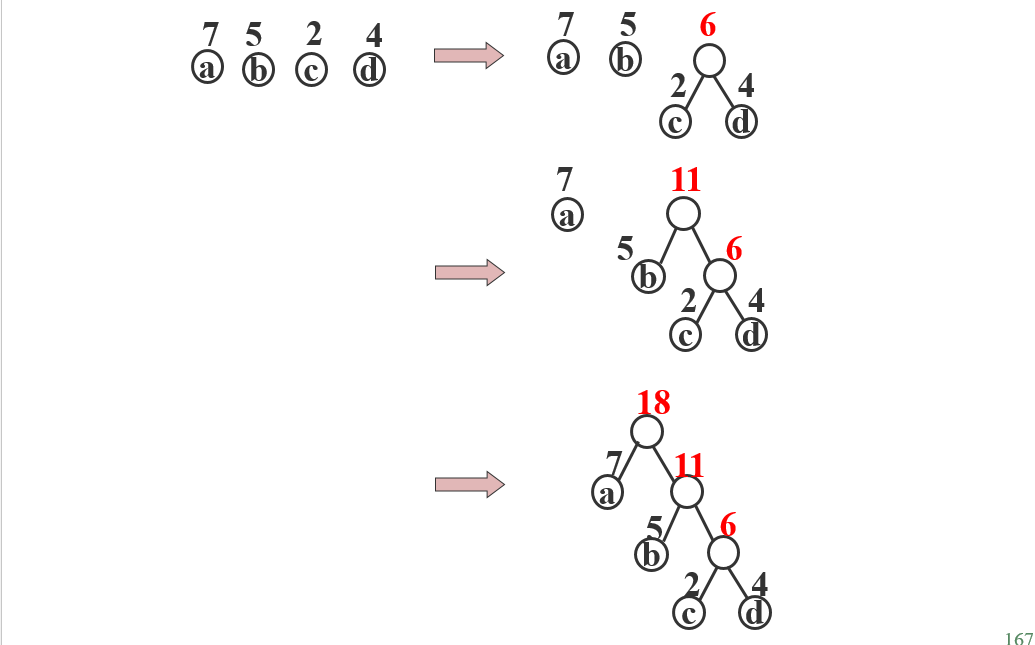
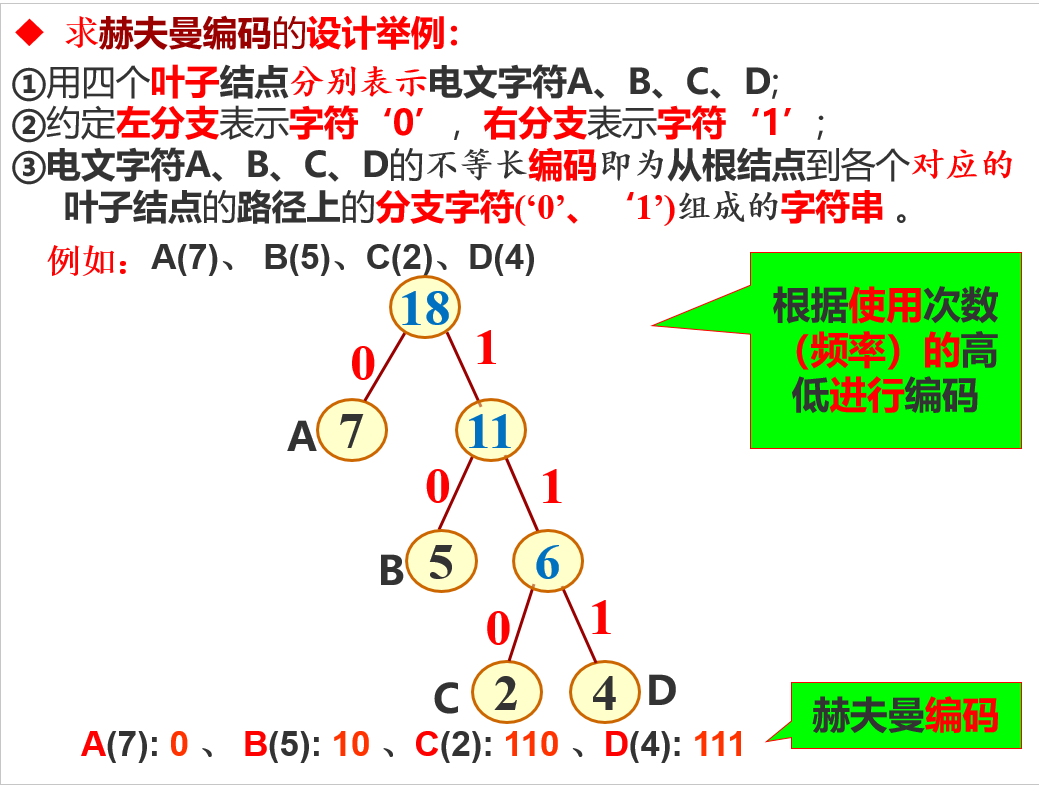
赫夫曼编码



 浙公网安备 33010602011771号
浙公网安备 33010602011771号