线性表

2.1 定义

定义：是由n个类型相同的数据元素构成的有限序列（例如：a1, a2, …， ai-1， ai， ai+1， …， an）。其中，每个数据元素它可以是一个整数或者一个字符，也可以是一个结构体类型数据等。线性表是一个数学模型，它是一个逻辑结构。

 

线性表的特点：

  • 同一性：是由同一类型的数据元素组成，即 ai 属于同一数据对象

  • 有穷性：由有限个数据元素组成；n=0时称为空表

  • 有序性

线性表可进行的操作：插入、删除、查找、遍历

 

 

2.2 顺序表示和实现（顺序表）

用一组地址连续的存储单元依次存储线性表中的数据元素。以元素在计算机内的存储物理位置相邻来表示线性表中的数据元素之间的逻辑关系

特点：

  1. 逻辑上相邻，物理位置相邻

  2. 可以随机存取

  3. 可以用静态或动态一维数组实现

 

顺序表的结构包含：指向线性表起始位置的指针，顺序表长度，顺序表容量

 

插入操作

算法思想：

  1. 检查i值是否超出所允许的范围（1 ≤ i ≤ n+1），若超出，则进行“超出范围”错误处理；

  2. 将线性表的第i个元素和它后面的所有元素均向后移动一个位置；

  3. 将新元素写入到新空出的第i个位置上；

  4. 顺序表的长度增1。

时间复杂度：

假设在第 i 个位置之前插入的概率为Pi，则在长度为n的顺序表中插入一个元素所需移动元素次数的期望值为：

$$
E_{is}=p1* n+p2*(n-1)+…pn *1+p(n+1)*0
$$

若假定在顺序表中任何一个位置上进行插入的概率都是相等的，则移动元素次数的期望值为：

 

 

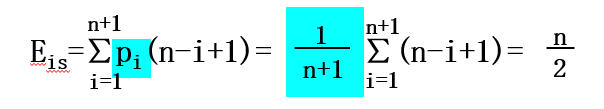
因而，该算法的时间复杂度为O(ListLength(L))

 

删除操作

算法思想：

  1. 在顺序表中删除第i个元素，并用e返回其值

  2. 将被删除元素位置之后的元素左移

  3. 表长减1

时间复杂度：

假设删除第 i 个元素的概率为 qi, 则在长度为n 的顺序表中删除一个元素所需移动元素次数的期望值为：

$$
E_{dl}=q1*( n-1)+q2*(n-1)+…q(n-1)*1+qn*0
$$

若假定在顺序表中任何一个位置上进行删除的概率都是相等的，则移动元素次数的期望值为：

 

 

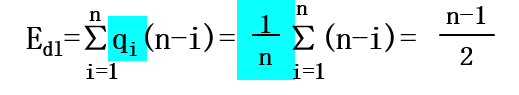
因而，该算法的时间复杂度为O(ListLength(L))

 

查找满足条件元素

算法思想：将顺序表中的元素逐个与给定值e比较操作

 

合并操作

算法思想1：

扩大顺序表LA，然后从顺序表LB 中依次取得每个数据元素，并依元素值在顺序表LA 进行查找，若不存在该值，则插入。

时间复杂度：O(La.length×Lb.length)

 

归并操作

初始条件：顺序表La 和Lb中数据元素必须均按值非递减有序排列 操作结果：归并La 和Lb得到顺序表Lc，使Lc中的数据元素也按值非递减有序排列

算法思想：

分别从La和Lb中取当前元素ai和bj；若ai<=bj，则将ai插入到Lc中，否则，将bj插入到Lc中。 亦即先将最小的插入Lc中，数据元素按值非递减有序排列

时间复杂度：O(La.length+Lb.length)

 

2.3 链式表示和实现（单链表）

单链表的特点：

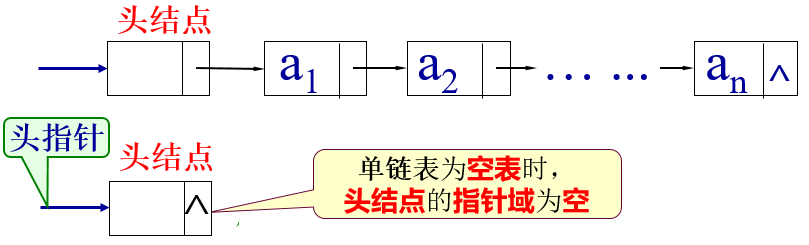
(1) 用一组地址任意的结点存储线性表中的数据元素， n个结点链成一个长度为n的线性链表。

(2) 每个结点除了存储数据元素本身，还设置了一个指针域，存放后继结点的指针，以此表示每个数据元素与其直接后继数据元素之间的逻辑关系。

(3) 结点的存储结构包含有两个域：数据域和指针域。

 

单链表类型的定义

 1 typedef struct  LNode {
 2       ElemType          data;         // 数据域
 3       struct LNode   *next;       // 指针域
 4    } LNode, *LinkList;  
 5 
 6 等价于：
 7 struct  LNode
 8  {    ElemType           data;    
 9       struct LNode *   next;   
10  } ；
11 //typedef struct  LNode  LNode； 
12 typedef   LNode *   LinkList； 
13 
14 LinkList L;

 

 

 

创建操作（逆序）

算法思想：

 

取第i个数据元素

算法思想：

p指向结点，j为计数器，同时移动p和j

时间复杂度：O(n)

 

插入操作

算法思想：

(1)必须先要找到单链表中第i-1个结点，此时第i-1个结点的指针域存放着第i个结点的地址。 (2)先需要将待插新结点的指针域存第i个结点地址以掌握后面的表。 (3)再修改第i-1个结点的指针域使其存要插入的新结点的地址，完成插入。

 

删除操作

算法思想：

（1）找到单链表中第i-1个结点, 用p指着第i-1个结点。 （2）修改第i-1个结点指针域之前需用q指着第i个结点。 （3）修改指针域,删除原来第 i-1个结点之后的结点。

 

归并操作

 

 

 

2.4 其他形式的链表

循环链表

最后一个结点的指针域的指针指向头结点的链表

与单链表的差别：判别链表中结点为最后一个结点的条件：不是后继是否为空，而是后继是否为头结点。

双向链表

在每个结点中有两个指针域：其一指向直接后继，另一指向直接前驱。

 
posted @ 2022-12-14 09:59  程序圆CodeStar  阅读(166)  评论(0)    收藏  举报