图(一)：无向图的深度优先遍历、广度优先遍历及连通分量

无向图：

一些关于图的定义：

图是由一组顶点和一组能够将两个顶点相连的边组成。

连通图：如果从任意一个顶点都存在一条路径到达另一个任意顶点，就称为连通图，一个非连通图由若干连通的部分组成，都称为极大连通子图。

无向图：即连接两个顶点的边是没有方向的。

 

无向图的数据结构：

使用邻接表来表示图：

 

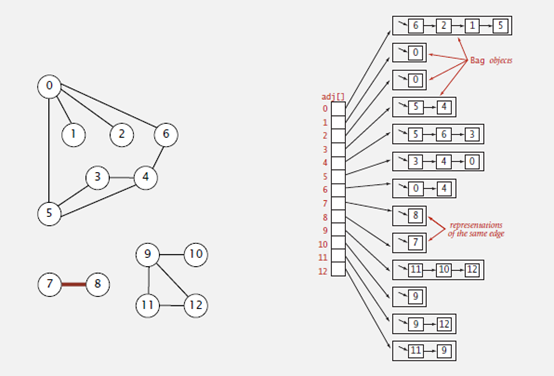
如上图所示，使用一个链表数组来表示图，其中数组的索引表示所有的顶点，每个数组中存放的链表表示所有与此顶点相连的顶点，也可以理解为边。

 

数据结构如下：

先看链表：

public class LinkedList<T> {
    private Integer N = 0;
    private Node<T> root;
    
    //链表的结点
    @SuppressWarnings("hiding")
    class Node<T> {
        T value;
        Node<T> next;
        
        public Node(T t,Node<T> node) {
            this.value = t;
            this.next = node;
        }
    }
    
    //添加一个结点
    public void add(Node<T> node) {
        if(root == null)
            root = node;
        else {
            Node<T> temp = root;
            root = node;
            root.next = temp;
        }
        N++;
    }
    
    public void add(T t) {
        Node<T> node = new Node<T>(t,null);
        if(root == null)
            root = node;
        else {
            Node<T> temp = root;
            root = node;
            root.next = temp;
        }
        N++;
    }
    
    //链表的节点数
    public Integer size() {
        return N;
    }
    
    public Node<T> getRoot() {
        return root;
    }
    
    
    //遍历链表
    public void traverse() {
        Node<T> node = root;
        while(node != null) {
            System.out.print(node.value + " ");
            node = node.next;
        }
    }
    
    
    //获取链表上的所有节点的值，返回一个数组
    public Integer[] getAllValue(LinkedList<T> linkedList) {
        if(linkedList.root == null)
            return null;
        
        Integer[] result = new Integer[linkedList.size()];
        Node<T> node = linkedList.root;
        Integer i = 0;
        while(node != null) {
            result[i++] = (Integer)node.value;
            node = node.next;
        }
        return result;
    }
}

 

图的数据结构：

public class UndiGraphBase {
    //顶点数目
    private Integer V;
    
    //边的数目
    private Integer E;
    
    //邻接表
    public LinkedList<Integer>[] adj;
    
    //创建一个含有V个顶点但不含有边的图
    @SuppressWarnings("unchecked")
    void graph(Integer V) {
        this.V = V;
        this.E = 0;
        adj = (LinkedList<Integer>[]) new LinkedList[V];
        for(int v=0;v<V;v++) {
            adj[v] = new LinkedList<Integer>();
        }
    }
    
    public Integer V() {
        return V;
    }
    
    public Integer E() {
        return E;
    }
    
    
    //添加一条边
    public void addEdge(Integer v,Integer w) {
        adj[v].add(w);
        adj[w].add(v);
        E++;
    }
    
    //遍历
    public void traverse() {
        for(int i=0;i<V;i++) {
            System.out.print(i + ": ");
            adj[i].traverse();
            System.out.println();
        }
    }
    
    
    //获取某个顶点所有相邻的顶点
    public Integer[] getAllValueByIndex(Integer i) {
        return adj[i].getAllValue(adj[i]);
    }
}

 

只要静下心来看，这些代码都比较简单，并且都有注释，就不多说了。

 

深度优先遍历

深度优先遍历类似于一个人走迷宫：

 

如图所示，从起点开始选择一条边走到下一个顶点，没到一个顶点便标记此顶点已到达。

当来到一个标记过的顶点时回退到上一个顶点，再选择一条没有到达过的顶点。

当回退到的路口已没有可走的通道时继续回退。

 

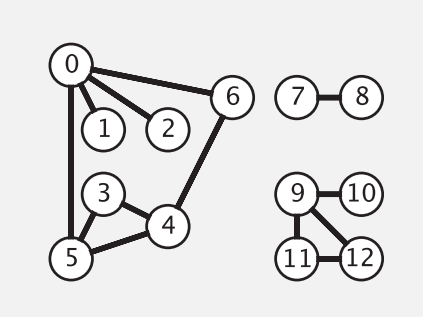
先给出一个已经构建好的图，之后的代码都建立在这个图的实例上：

 

public class Instance {
    public static UndiGraphBase getInstance() {
        UndiGraphBase undiGraphBase = new UndiGraphBase();
        undiGraphBase.graph(13);
        undiGraphBase.addEdge(0, 5);
        undiGraphBase.addEdge(4, 3);
        undiGraphBase.addEdge(0, 1);
        undiGraphBase.addEdge(9, 12);
        undiGraphBase.addEdge(6, 4);
        undiGraphBase.addEdge(5, 4);
        undiGraphBase.addEdge(0, 2);
        undiGraphBase.addEdge(11, 12);
        undiGraphBase.addEdge(9, 10);
        undiGraphBase.addEdge(0, 6);
        undiGraphBase.addEdge(7, 8);
        undiGraphBase.addEdge(9, 11);
        undiGraphBase.addEdge(5, 3);
        return undiGraphBase;
    }
}

 

 

 

该实例表示的图如下：

 

深度遍历的顺序如下图所示：

 

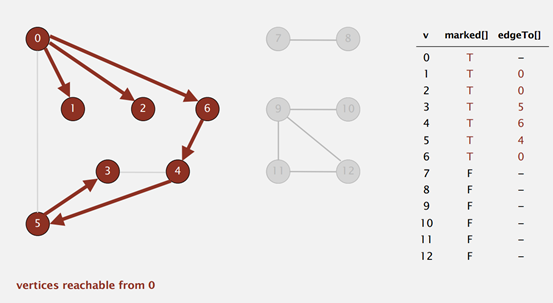
数组marked表示索引所代表的顶点是否被访问过

数组edgeTO[]表示到达索引所代表的顶点的上一个顶点，通过对此数组的处理即可得到路径，即可以用循环，也可以用栈，因为知道每个顶点的上一个顶点，所以可以得到路径

 

遍历的代码如下：

public class DepthFirstPath {
    //所有顶点组成的数组，如果起点到某顶点可达，则为true，否则为false
    private boolean[] marked;
    
    //起点
    private final Integer startV;
    
    //用数组来表示路径树，表示起点到可达顶点的路径。保存的是到达此顶点的上一个顶点
    private Integer[] edgeTo;
    
    public DepthFirstPath(UndiGraphBase G,Integer startV) {
        marked = new boolean[G.V()];
        edgeTo = new Integer[G.V()];
        this.startV = startV;
        dfs(G,startV);
    }
    
    public void dfs(UndiGraphBase G,Integer v) {
        marked[v] = true;
        Integer[] allNodeValues = G.getAllValueByIndex(v);
        if(allNodeValues == null)
            return;
        
        for(int i=0;i<allNodeValues.length;i++) {
            if((!marked[allNodeValues[i]])) {
                edgeTo[allNodeValues[i]] = v;
                dfs(G,allNodeValues[i]);
            }
        }
    }
    
    
    //获取顶点到v的路径
    public void getPath(UndiGraphBase G,Integer v) {
        if(!hasPathTo(v))
            return;
        
        //存储路径
        Stack<Integer> path = new Stack<Integer>();
        for(int i=v;i!=startV;i = edgeTo[i])
            path.push(i);
        
        //加入起点
        path.push(startV);
        
        //打印栈（即起点startV到v的路径）
        System.out.println(path.toString());
    }
    
    //从起点startV是否有路径通往v（即是否可达）
    public boolean hasPathTo(Integer v) {
        return marked[v];
    }
    
    public static void main(String[] args) {
        UndiGraphBase G = Instance.getInstance();
        DepthFirstPath depthFirstPath = new DepthFirstPath(G,0);
        depthFirstPath.getPath(G, 3);
    }
}

 

其实整个代码是比较好懂的，主要是edgeto数组需要理解一下。

 

 

广度优先遍历

广度优先遍历其实比深度优先遍历好理解，即从起点开始，遍历所有与起点连通的顶点，再遍历与这些顶点连通的顶点，即先搜索距离起点距离为1的顶点，再遍历与起点距离为2的顶点.....

 

 

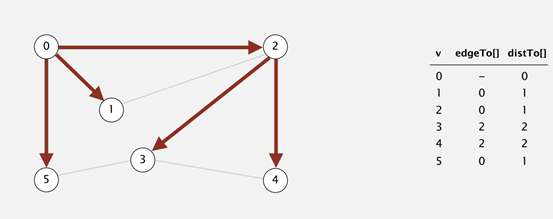
其中经edgeTo数组的意义与深度优先中edgeTo数组一样。

而distTo[]数组则表示与起点的距离，图中使用该数组只是为了便于理解，代码中可以不用，因为距离可以通过遍历edgeTO[]数组得到

 

广度优先遍历的代码：

 

public class BreadthFirstPath {
    //到达该顶点的最短路径是否已知
    private boolean[] marked;
    
    //到达该顶点的已知路径上的最后一个顶点
    private Integer[] edgeTo;
    
    //起点
    private final Integer start;
    
    public BreadthFirstPath(UndiGraphBase G,Integer start) {
        marked = new boolean[G.V()];
        edgeTo = new Integer[G.V()];
        this.start = start;
        bfs(G,start);
    }
    
    private void bfs(UndiGraphBase G,Integer start) {
        Queue<Integer> queue = new java.util.LinkedList<Integer>();
        //标记起点
        marked[start] = true;
        queue.add(start);
        
        while(!queue.isEmpty()) {
            //从队列中删除下一顶点
            Integer v = queue.remove();
            
            Integer[] allNodeValues = G.getAllValueByIndex(v);
            for(int i=0;i<allNodeValues.length;i++) {
                //对于每个未被标记的顶点
                if(!marked[allNodeValues[i]]) {
                    //保存最短路径的最后一个顶点
                    edgeTo[allNodeValues[i]] = v;
                    //标记它，因为最短路径已知
                    marked[allNodeValues[i]] = true;
                    queue.add(allNodeValues[i]);
                }
            }
        }
    }
    
    public boolean hasPathTo(Integer v) {
        return marked[v];
    }
    
    //获取顶点到v的路径
    public void getPath(UndiGraphBase G,Integer v) {
        if(!hasPathTo(v))
            return;
        
        //存储路径
        Stack<Integer> path = new Stack<Integer>();
        for(int i=v;i!=start;i = edgeTo[i])
            path.push(i);
        
        //加入起点
        path.push(start);
        
        //打印栈（即起点startV到v的路径）
        System.out.println(path.toString());
    }
    
    public static void main(String[] args) {
        UndiGraphBase G = Instance.getInstance();
        BreadthFirstPath breadthFirstPath = new BreadthFirstPath(G,0);
        breadthFirstPath.getPath(G, 3);
    }
}

 

 

 

 

使用深度优先遍历获取图中的所有连通分量

 

public class ConnectedComponent {
    //顶点是否联通
    private boolean[] marked;
    
    //联通分量标识符
    private Integer[] id;
    
    //联通分量数目
    private Integer count = 0;
    
    public ConnectedComponent(UndiGraphBase G) {
        marked = new boolean[G.V()];
        id = new Integer[G.V()];
        for(int i=0;i<G.V();i++) {
            if(!marked[i]) {
                dfs(G,i);
                count++;
            }
        }
    }
    
    public void dfs(UndiGraphBase G,Integer v) {
        marked[v] = true;
        id[v] = count;
        
        Integer[] allNodeValues = G.getAllValueByIndex(v);
        for(int i=0;i<allNodeValues.length;i++) {
            if((!marked[allNodeValues[i]]))
                dfs(G,allNodeValues[i]);
        }
    }
    
    //判断v和w是否联通
    public boolean connected(Integer v,Integer w) {
        return id[v] == id[w];
    }
    
    //连通分量数
    public Integer count() {
        return count;
    }
    
    //v顶点所在的联通分量的标识符（0-count()-1）
    public Integer id(Integer v) {
        return id[v];
    }
    
    public Integer[] getID() {
        return id;
    }
    
    public static void main(String[] args) {
        UndiGraphBase G = Instance.getInstance();
        ConnectedComponent cc = new ConnectedComponent(G);
        
        Integer m = cc.count();
        System.out.println(m + " components");
        
        Integer[] id = cc.getID();
        
        for(int j=0;j<m;j++) {
            for(int i=0;i<id.length;i++) {
                if(id[i] == j) {
                    System.out.print(i + " ");
                }
            }
            System.out.println();
        }

    }
}

 

 

 

 

其中marked数组表示索引所代表的顶点是否已经被访问

Id数组表示索引所代表的顶点属于哪个连通分量，假如一个图总共有n个分量，那么各个连通分量分别用0,1,2....n-1表示，id数组的值即是该顶点属于第几个连通分量。

 

 

广度优先遍历与深度优先遍历的区别

深度优先遍历不断深入图中并在栈中保存了所有分叉的顶点；广度优先遍历则像扇面一般扫描图，用一个队列保存访问过的最前端的顶点。深度遍历的方式是寻找离起点更远的顶点，只在碰到死胡同时才访问进出的顶点，广度遍历则会首先覆盖起点附近的顶点，只在临近的顶点都被访问完后，才去访问更远的顶点。

深度优先遍历的路径通常较长而曲折，广度优先遍历的路径通常短而直接。

 

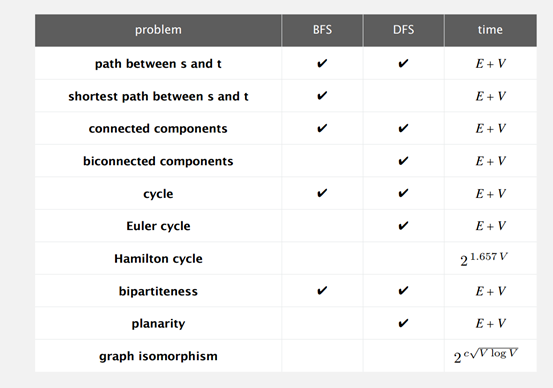
关于广度优先遍历和深度优先遍历的使用场景与效率如下图所示：