【集合论】 03 - 序集和序数
1. 势
在上一篇我提过自然数“量”和“序”的双重性质,如果再仔细斟酌,“量”其实是由“序”产生和决定的,把有限的元素按某个顺序排列起来,正是我们确定其数量的过程。那么对于无穷集,“量”和“序”还有这样的关系吗?无穷集的“量”和“序”又该如何定义呢?既然它们产生于自然数,那么答案自然就在自然数的扩展中。对于有限集的量\(n\),可以看作是有限集的元素与\(n\)的元素的一一对应。这个直观的方法同样适用于无穷集,如果能找到一个标尺,将无穷集的元素和标尺的元素一一对应,那就能得到无穷集的“量”。
暂且不管这个标尺是什么,我们需要先检验这个方法的合理性,至少“相等”是可以被定义的。直觉上我们往往采用大小或包含关系来推导集合是否一样大,但这样的直觉却是不可靠的,也不是一种良性的定义,数学上需要“好”的定义。对于存在一一映射的两个集合\(A\)、\(B\)称其为等势(equinumerous),记做\(A\approx B\),容易证明,等势可以作为“量相等”的定义。有时可以找到一些函数,使得局部和整体能一一映射,比如\(2n\)映射了自然数和偶数,\(\cot\pi x\)映射了\((0,1)\)和实数\(\Bbb R\),所以它们也是“一样大”的。
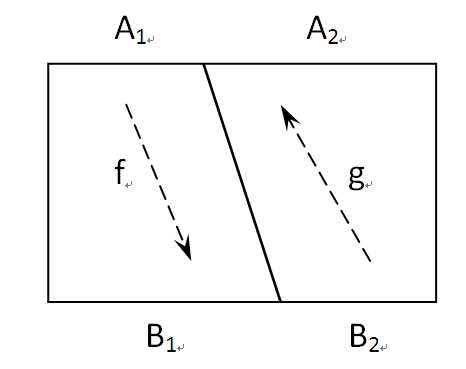
“大于”、“小于”也可以用类似的方法定义:如果从集合\(A\)到集合\(B\)存在单射,则称\(A\)受制于\(B\),记作\(A\preccurlyeq B\)。如果\(A\)、\(B\)不等势,称\(A\)严格受限于\(B\),记作\(A \prec B\)。受制的良性需要保证,这就是如下的SB定理(Schröder-Bernstein)。证明中假设分别有单射\(f:A\to B\)和\(g:B\to A\),需要构造\(A\)、\(B\)的分割,使得\(f(A_1)=B_1\)、\(g(B_2)=A_2\)。对\(X\in A\),记\(X^*=A-g(B-f(X))\),从\(A\)开始逐渐缩小\(X\),并保证\(X^*\subseteq X\),最小的那个(满足条件的\(X\)的交)便是\(A_1\)。SB定理是判断集合等势的有力武器,用它可以轻松证明任何区间都与实数集\(\Bbb R\)等势。有受制关系的集合称为可较的,它是比较集合大小的“好”定义,但问题是所有集合都可较吗?这个问题需要暂且搁置,后面再提。
\[A\preccurlyeq B\wedge B\preccurlyeq A\Rightarrow A\approx B\]
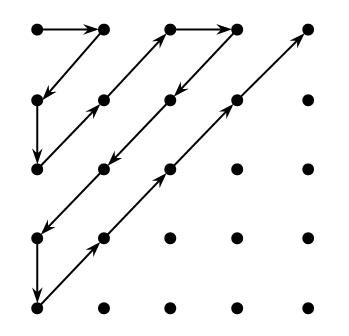
利用等势,“有限”和“无穷”就可以被精确定义了:和某个自然数等势的集合称为有限集,否则称为无穷集。这个定义的良性也是需要证明的,即证不同的自然数不等势(需用归纳原理),从而有限集\(A\)只与一个自然数等势,这个自然数也叫集合的势,记作\(N(A)\)。用归纳原理可以证明有限集\(A\)的真子集\(B\)也是有限集,且有\(N(A)>N(B)\)。反之,如果集合与其真子集等势,则它必是无穷集,这也可以作为无穷集的定义。无穷集中以\(\omega \)最为特殊,受制于\( \omega \)的集合叫可数集,它的每个元素都可以被“数”到。偶数集、整数集\(\Bbb Z\)等都是可数集(容易证明),由下图还可以证明\(\omega\times \omega\)可数,即可数个可数集可数,这个结论可以直接推到2维、3维...可数维空间的整数点都是可数的。有理数都可以表示成分数,而分数可看作2维空间的子集,所以有理数集\(\Bbb Q\)也是可数的。
那么有没有不可数的无穷集呢?康托尔本人给出了否定的答案,这就是著名的“对角论证法”。这里稍作修改,考虑区间\([0,1)\),假设它是可数的,用二进制数表示它们。再构造一个数\(x\),它的第\(i\)位小数与\(a_i\)的第\(i\)位小数相反,则\(x\)不能被数到,矛盾。一般地有,任何集合的幂集与该集合不等势(\(X\prec\mathscr P(X)\)),证明思想和“对角证明法”如出一辙。假设存在一个一一映射\(f:X\to\mathscr P(X)\),构造\(B=\{x\in X|x\in f(x)\} \),则\(B\)没有原像(反证),矛盾。由于\(\mathscr P(X)\approx 2^X\),该定义还可以写成\(X\prec 2^X\),从而任何集合都有比它还“大”的集合。

\(\omega \)的势一般用\(\aleph _0\)表示,\(\Bbb R\)的势一般用\(C\)表示,\([0,1]\)的二进制表示可以看做是自然数子集的比特表示,所以有\(\Bbb R\approx 2^{\omega}\)和\(C= 2^{\aleph _0}\)。\(\aleph _0\)是最小的无穷势,假设下一个无穷势记作\(\aleph _1\),那么它会是\(C\)吗?更一般地问题是,是否有\(2^{\aleph _{\alpha}}=\aleph _{\alpha +1}\)?这就是著名的连续统假设(CH,Continuum Hypothesis,\((0,1)\)称为连续统)和广义连续统假设,由康托尔提出并尝试证明,但并未完成。希尔伯特(Hilbert)在1900年提出了20世纪待解决的23个重要数学问题,连续统假设被列在问题之首。后来哥德尔证明了它与ZFC的兼容性,科恩(Cohen)用力迫法证明了其独立性,也就是说连续统假设并不能在ZFC系统内证明,但至今仍未找到合适的公理使其成立。


Hilbert(1862 - 1943) Cohen(1934 - 2007)
2. 良序
有一个常用的证明方法,它从给定的一簇集合中各选取一个代表元素,这些元素能否组成集合并不能由前面的公理推得。策梅洛为这个方法专门提出了选择公理(AC),后人证明了AC与ZF的兼容性和独立性。当集合数量无穷时,这样的操作并不能通过有限步的推理完成,因此这个方法一直被构造派所抵制。但数学中的很多重要结论都无法绕开AC,甚至反对者自己也在不自觉地使用着它,后来反对的声音自然也就变弱了。AC可以从之前的概念中得出许多有用的结论,比如如果存在满射\(f:A\to B\),则存在单射\(g:B\to A\),再比如无穷集中可以抽取出和\(\omega\)等势的子集,从而无穷集总是和其真子集等势(可以做无穷集的定义)。
【ZFC-8】选择公理(Atom of Choice):对集簇\((A_i)_{i\in I}\),存在簇\((a_i)_{i\in I}\)。
现在继续讨论对自然数的扩展,以得到我们的标尺,标尺上是有序排开的刻度。满足自反性、反对称性和传递性的关系称为偏序(partial order),偏序中可以方便地引入\(\leqslant\)、\(<\)等符号,它们将元素组成了一个网状。标尺当然要是线状的,这需要每个元素都可较,这样的偏序称为全序(total order)或线性序(linear order)。要扩展自然数,它还要满足最小数原理(任何子集有最小元),这样的全序叫良序(well order),良序集几乎包含了自然数的所有特性。对于线状的全序,截取其左边部分称为截断,而\(s(a)=\{x\in A|x<a\}\)称为\(a\)在\(A\)中的前段(initial segment),不同于截断的是,前段都有一个“后继者”。由最小数原理容易得知良序的截断都是前段,这是它区别于一般全序的重要特性,并由此可以得出以下的超限归纳原理和超限递归原理:
超限归纳原理(Transfinite Induction Principle):若\(A\)是良序\(W\)的子集,且有\(\forall a\in W(s(a)\subset A\Rightarrow a\in A)\),则\(A=W\)。
超限递归原理(Transfinite Recursive Theorem):存在满足递归定义\(u_a=f(u\restriction s(a))\)的函数。
结构相同(同构)的良序可以看做是“相等”的,准确地说对于良序\((X,\leqslant _X)\)和\((Y,\leqslant _Y)\),如果存在双射\(f:X\to Y\)使得\(a\leqslant _Xb\Leftrightarrow f(a)\leqslant _Yf(b)\),则称\(X\)、\(Y\)相似(isomorphic),记作\(X \simeq Y\)。可以直观地想象,全序集上的相似映射可以左右移动,但有头无尾的偏序只能向右移动,从而良序到其子集的相似映射总有\(x\leqslant f(x)\),进而可以得出良序不能和其截断相似和良序间相似映射的唯一性。对于任意两个良序的比较,自然是选择头部对齐,看看谁更长,由超限递归原理容易证明它们要么相似,要么一个相似于另一个的前段。
标尺的框架(良序)已经有了,一个自然的问题是,任何集合的元素都可以对应到标尺的刻度上吗?换句话说,任何集合都可以良序化吗?康托尔提出了这个问题(良序化原理),但却未能解决,策梅洛提出了选择公理并给出了证明。证明过程完全基于选择公理,并反复用到超限归纳原理,只是要注意归纳原理仅作用于良序,证明中需要一些常用技巧和处理。有了良序化原理,就可以回答任何集合是否可较的问题,因为任何集合可以良序化,而良序集可较,所以任何集合可较,即\(A\approx B\)、\(A\prec B\)和\(B\prec A\)恰有其一成立(三歧性)。
良序原理可以得到另一个基本结论,它就是Zorn引理:如果序集的任意链有上界,则它有极大值。证明中可以将\(M\)良序化来构造想要的极长链,从而得到极大值。在没有选择公理和良序原理时,如果承认Zorn引理,也是可以证明选择公理的,它等价于证明一个关系中有一个定义域相同的函数,可以通过将所有函数组成包容序来解决。至此,选择公理、良序原理和Zorn原理可互相推导,它们可以看做是等价的。
3. 序数和基数
标尺的框架和可行性已经解决了,接下来就是来标刻度了。按照自然数的定义,我们自然想到这些刻度应该是\(1,2,3,\cdots ,\omega ,\omega ^+,\cdots\),但想用一句话概括它们还是得有严格的定义:满足条件\(\forall x\in\alpha (s(x)=x)\)的良序集\(\alpha\)称为序数。容易证明自然数都是序数,而且如果\(\alpha\)是序数,则\(\alpha ^+\)也是序数,所以\(\omega ,\omega ^+,\cdots\)都是序数。容易证明任何序数中都含有\(0\),而且其元素也是序数,用超限归纳原理还可以证明相似的序数必是相等的,从而序数的“唯一性”就得到了保证。序数都是良序集,它们也就满足三歧性,所以它们可以一字排开,而且每个序数的“后序数”都是它的后继者。
那么还有最后一个问题:所有集合(或良序集)都有其对应的序数吗?回答这个问题之前需引进另一个公理,这就是下面的替换公理。替换公理在没有限制集的情况下承认一类集合的存在,因为这类集合受制于已知集合,它们的存在也是合理的。但替换公理却不是独立于其它公理的,它可以完全取代子集公理,它还可以证明偶集公理。ZFC公理系统还有最后一个略显多余的正则公理,它避免了过大集合的产生,但其它9条公理其实构造不出那样的集合。
【ZFC-9】替换公理(Atom Schema of Replacement):如果给定集合的任一元素都有唯一的集合与之对应,这些集合可以组成集合。
\[\forall x\in A,\forall y_1\forall y_2(\varphi (x,y_1) \wedge\varphi (x,y_2)\Rightarrow y_1=y_2)\Rightarrow\exists B=\{y|\exists x(\varphi (x,y))\}\]
【ZFC-10】正则公理(Atom of Regularity):对任意非空集合\(A\),存在一个元素\(x\)使得\(x\cap A=\varnothing\)。
\[\forall A\exists x(x\in A\wedge x\cap A=\varnothing)\]
有了替换公理就可以构造良序集的序数了,考察良序集中那些有序数的前段,这些序数的并(替换公理)就是要找的序数,这就是我们要的计数原理:任何良序集\(X\)都相似于唯一序数\(\alpha\),记作\(\alpha ={\rm ord}(X)\)。序数可以作为自然数的扩展,不是自然数的序数叫超限数,可以按如下方法定义序数的加法和乘法,它们满足大部分运算定律,但乘法不满足交换律和右分配律。
(1)\(\alpha +\beta ={\rm ord}(\hat\alpha\cup\hat\beta )\),其中\(\hat\alpha =\{(x,0)|x\in\alpha\}\)、\(\hat\beta =\{(1,y)|y\in\beta\}\);
(2)\(\alpha\cdot\beta ={\rm ord}(\alpha\times\beta )\)。
序数仅能扩展自然数“序”的性质,但却不能体现“量”的性质,因为不同的序数可以是等势的。这些等势的序数有最小者,把它作为“量”的度量,称为基数(cardinal number),记作\({\rm card}(X)\)。基数是势的量化描述,非自然数的基础称为超限基数,显然\(\aleph _0\)是最小的超限基数。由序数原理自然可知每个序集都有都有对应基数,这样SB定理变得十分显然,但要知道序数定理是基于选择公理的,而SB定理本身不依赖选择公理。基数的加法、乘法和幂都容易定义,以及一般的运算律都容易证明,这里不再赘述,值得一提的是以下运算律,它们可以通过Zorn引理和反证来证明。
(1)加法吸收律:\(b\)为超限基数,且\(a\leqslant b\),则\(a+b=b\);
(2)乘法吸收律:\(b\)为超限基数,且\(1\leqslant a\leqslant b\),则\(a\cdot b=b\);
(3)幂的降底律:\(b\)为超限基数,且\(2\leqslant a\leqslant b\),则\(a^b=2^b\)。
看起来我们在无穷的道路上已经走远,但其实这只是个开始,当沿着\(\omega ,2\omega ,\cdots ,{\omega ^2},{\omega ^3},\cdots ,{\omega ^\omega},{\omega ^{{\omega ^\omega}}},\cdots\)一路思考下去,你将彻底迷失……
【全篇完】



