【几何基础】04 - 比例和面积
希尔伯特的五组几何公理,描述了一个与欧几里得空间等价的几何空间,然而这套公理的价值远非如此。它的目的更在于分离出几何空间中最本质的内涵,对其精简分类,以突出每一个内涵的价值。所以到此为止,几何系统的讨论非但没有结束,而是才刚刚开始。在前几篇的定理讨论中,我们明确了这样一个事实:每个定理的成立都有其依赖的最小公理集。解析每个定理背后的公理,而不是在整个系统中讨论,更能洞察出定理的本质是什么。
1. 比例论
1.1 帕斯卡定理
上篇的最后我们提到过,公理\(V\)(连续公理)更多地是为了向欧几里得空间收敛,它在一般几何空间的讨论中是经常被忽略的。本篇就试图在公理\(V\)缺席的情况下(非阿基米德几何),继续讨论线段的比例和图形的面积,以展示:这两个概念是几何空间的内在属性,而非一定要依赖于实数系统。由于讨论范围限定在一个平面之中(平面几何),这里暂时也可以先拿掉空间公理\(I_{3\sim 6}\),也就是说本篇的讨论仅基于公理\(I_{1\sim 2},II\sim IV\)。其实公理\(II_3\)包含了空间公理中的\(I_3,I_5\),所以真正去除的只是宣称空间维度的\(I_4,I_6\)。
不论是线段比例还是图形面积,都避不开线段“乘法”的定义,为了不使用实数系统,这里先要用线段定义出“线段乘法”。而合适的定义要基于一个众所周知的定理:帕斯卡定理(教材译作巴斯噶),它的内容如下:有两条相交直线,记\(A,B,C\)和\(A',B',C'\)分别是两条线上的点,它们都不是交点且有\(AB'\mathop{//}A'B,\,AC'\mathop{//}A'C\),则一定有\(BC'\mathop{//}B'C\)。注意,该定理并不要求三点在交点的同一侧,你可以画出完全不同于以下左图的情况。
在欧几里得空间,由平行关系得到有向线段积\(OA\cdot OA'=OB\cdot OB'\)和\(OA\cdot OA'=OC\cdot OC'\),再有\(OB\cdot OB'=OC\cdot OC'\)并得到\(BC'\mathop{//}B'C\)。教材上使用了类似的思路,但是为了避开比例计算,借助全等判定定理定义了边角的“乘法关系”,具体细节这里就不展开了。有意思的是,书中还提到,帕斯卡定理可以只依赖公理\(I\sim III\)便得以证明,也即加入空间公理、去除平行公理。希尔伯特的证明中,使用到四点共圆的性质,而这依赖于平行公理(对三点在交点一侧的简化证明,更是反复使用了四点共圆)。
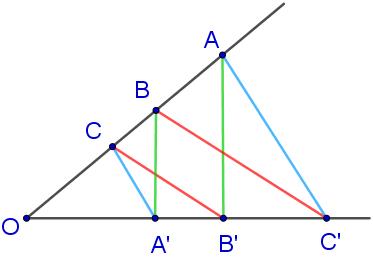
1.2 乘法和比例
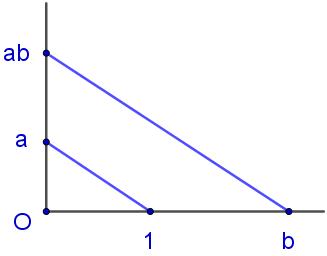
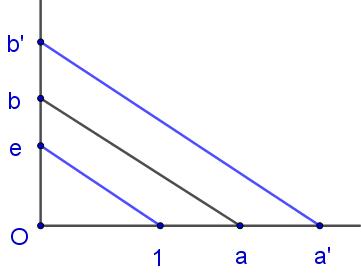
现在来定义由线段组成的“代数系统”,以在没有实数系统的情况下定义比例和面积。首先把线段合同定义为元素的“相等”,线段的拼接定义为元素的“加法”,线段的大小定义为元素的“大小”。不难证明这些元素(线段)满足交换律和结合律,任何单点线段就是零元(记作0)。定义乘法时,先要规定好单位线段(记作1),然后把\(1,a,b\)如上右图迁移到一个直角上,平行线在一边截取的线段定义为乘法\(ab\)。这个定义同样启发于欧几里得几何的相似比例,定义方法非常自然,1显然也符合单位元的性质(\(1a=a1=a\))。
接下来要小心求证乘法的交换律和结合律,它们并不是天然成立的,但证明过程并不复杂。先是如下左图,根据帕斯卡定理证得红线平行,从而\(ab\)的端点就是\(ba\)的端点,即\(ab=ba\)。然后考察以下右图,根据交换律和帕斯卡定理证得红线平行,从而\((ab)c=a(bc)\)。最后还有乘法加法分配律,通过线段的迁移和图形相等定理可以轻松得到(请自行画图作证)。有了乘法,反向也可以定义除法,\(a/b\)定义为满足\(a=bc\)的唯一线段\(c\)。
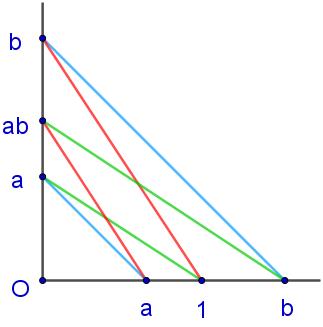
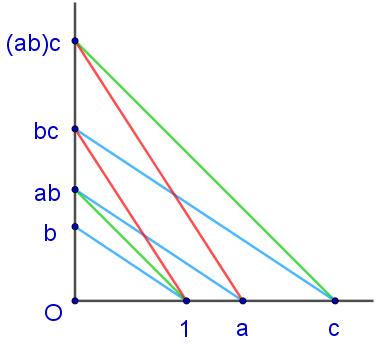
如果\(a/b=a'/b'\),也称它们是成比例的,记作\(a:b=a':b'\)。假设比值为\(e\),则有\(a=eb,a'=eb'\),不难得到\(ab'=a'b\)。反之由\(ab'=a'b\)也可证\(a:b=a':b'\)和\(a:a'=b:b'\),总结为式(1)。有了成比例的概念,就可以讨论三角形相似了,一般把三个角都相等(合同)的两个三角形称为相似的。由于乘法是在直角上定义的,只能先讨论相似直角三角形,如下左图,不难证明两条直角边是成比例的\(a:b=a':b'\)。对于一般三角形,先如下右图作出角平分线和垂线,分成的6个直角三角形都对应相似,从而容易有三角形三边成比例\(a:a'=b:b'=c:c'\)。
\[a:b=a':b'\;\Leftrightarrow\;ab'=a'b\tag{1}\]
这时我们再看乘法的定义,那个直角的要求是必需的,因为当时无法得知任意角上得到的“乘积”线段都是合同的。然而现在根据相似三角形的成比例性质可知,平行线在任意角上截下的线段都是是成比例的。也就是说,构造乘积线段时,再也不必须在直角上了。平行线截成比例线段的结论,还说明成比例并不依赖线段1的选取,它是图形的内在性质。为此教材的补篇II中,直接用平行线截直角的方法定义成比例,也能完整获得相似三角形的性质。
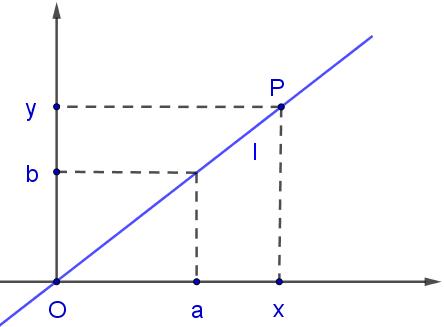
最后,如果想在这样的几何空间中定义笛卡尔坐标,就要对直线区分“正负”方向,也就是规定正负线段。这时线段的代数系统才能成为一个完整的“域”,并进行加减乘除的运算。建立平面坐标的方法也符合直观,指定两条垂直的有向直线(坐标轴),平面上任意一点的坐标定义为:点到坐标轴的垂线段\((Ox,Oy)\)(有向线段)。过原点\(O\)的直线上\(l\)任意一点满足\(x:y=a:b\)(下图),也即\(bx-ay=0\),它便是直线的方程。当然也容易有任意直线\l'\)的方程:\(bx-ay-c=0\),注意这里都还是线段运算,而非实数方程。
2. 图形面积
2.1 剖分相等、拼补相等
有了相似和比例的概念,自然就有了图形“大小”的概念,也就是这里要讨论的面积。但仅通过相似能得到的面积关系十分有限,这里以三角形为基本图形,通过合同的组合(简单加减法)讨论多边形的面积。当然这里的“多边形“”和“图形分割”也是需要严谨定义,请参考课本讨论,这里略去不述。还有在给出“面积相等”的定义时,在表述上一定要严谨,不能把直觉看作当然。首先因为用到三角形合同,就一定要合同公理在场,即使最终面积写成了线段乘法(乘法不一定要合同)。其次因为没有连续公理,做三角形的拆分、拼接时都只讨论有限个三角形的情况。
拆分和拼接看上去只是简单的加减法,但定义“面积相等”时,还不能天然地将它们混用。先定义单纯一些的拆分相等,即如果两个多边形可以拆分为有限个相互合同的三角形,那它们称为剖分相等的。这个定义十分自然,但要注意相等的传递性并不显然,需要展开讨论。假定多边形\(P_3\)分别和\(P_1,P_2\)剖分相等,也即\(P_3\)有两种三角形分割集\(\mathbf{T_1},\mathbf{T_2}\),它们分别可以组合成\(P_1,P_2\)。把\(\mathbf{T_1},\mathbf{T_2}\)都叠放在\(P_3\)中,将得到更碎小的多边形,可以把它们全部分割成三角形,得到分割集\(\mathbf{T_3}\)。显然\(\mathbf{T_3}\)就是\(P_1,P_2\)的一个共同分解,所以\(P_1,P_2\)剖分相等,剖分相等的传递性成立。
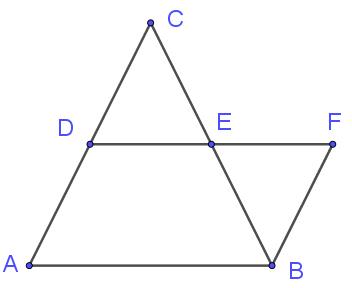
一个比较简单的剖分相等的例子是如下左图的\(\triangle ABC\)和平行四边形\(ABFD\),由此三角形和平行四边形可以在剖分相等的意义上相互替代。然而在试图分割一些简单的图形时,就会发现剖分相等非常局限,很难发挥作用。书上举了一个有趣的例子(如下右图),看似两个同底等高的平行四边形总可以剖分相等,但这个直觉论证中却引入了阿基米德公理。该公理不成立时(本篇不使用连续公理),可以成功举出反例。

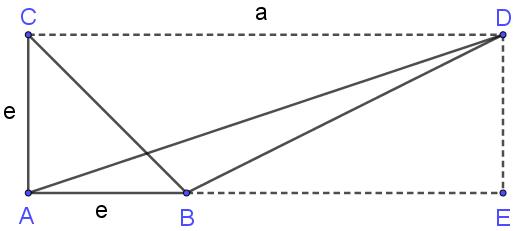
反例来自下图两个同底等高的三角形(等价于对应平行四边形的讨论),其中\(\angle CAB,\angle DEB\)都为直角,线段\(AE=a\)总有\(a>ne\)(非阿基米德几何)。如果\(\triangle ABC\)和\(\triangle ABD\)剖分相等,考察所有分解三角形的周长之和\(S\)。放在\(\triangle ABC\)里看,\(S\)不会超过\(e\)的有限倍(要用到三角形两边之和大于第三边,以及三角形内部线段不大于三角形最长边,请自行论证)。然而放在\(\triangle ABD\)里看,\(S\)一定大于\(AD\),继而\(S>a>ne\),导出矛盾。
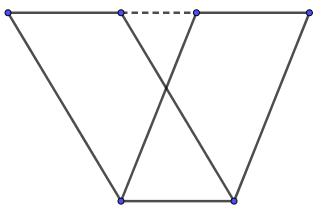
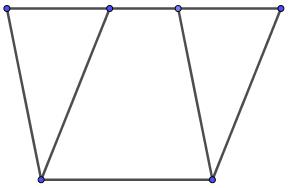
现在把剖分相等的概念拓展一下,如果两个多边形拼接上有限个相互合同的三角形后是剖分相等的,那么它们称为拼补相等的。拼补相等也需要证明传递性,过程略显繁琐,但基本原理和剖分相等类似。显然拼补相等包含了剖分相等(补上0个三角形),然而反直觉的是,拼补相等并不一定剖分相等。比如从下图可知,同底等高的平行四边形总是拼补相等的,从而同底等高的三角形也拼补相等,然而上图的反例则说明它们可能不剖分相等。以下面积讨论,一般都基于更宽泛的拼补相等。
在继续讨论多边形面积的度量(量化和比较)之前,先来看一个基础结论。首先对于任意三角形,它总可以和一个直角三角形拼补相等;以下左图说明,任何直角\(\triangle ABC\)都与某个“股1”的直角\(\triangle ABD\)拼补相等。从而任意三角形都与某个“股1”的直角三角形拼补相等,继而也有任意多边形都与某个“股1”的直角三角形拼补相等。但要特别注意,这个结论只是说相等存在,并没有说明唯一性和排它性,所以我们还不能把图形面积的比较转化为线段的比较。具体来说,还需要回答:底边相同的两个拼补相等的三角形,它们的高一定相等吗?


2.2 面积的度量
为此我们要找到多边形面积的唯一“度量”。考察\(\triangle ABC\)及其两个高\(AD,BE\)(以上右图),易证\(\triangle ADC\sim\triangle BEC\),从而有\(AC\cdot BE=BC\cdot AD\)。也就是我们所熟知的结论:三角形任意底边和其上的高的乘积是固定的,按照习惯可以把底高乘积的一半(线段)作为三角形面积的度量。对于一般多边形(包括三角形),可以分解为若干三角形,多边形面积的度量自然应当是这些小三角形面积的度量之和。但请注意,这里出现了线段的代数运算,而且需要证明:不同分割方法下得到的面积度量是一致的。
为了解决以上问题,需要给面积度量定好“方向”,直观地说就是给图形或平面规定正反面。我们知道一条直线把平面分成了两部分,如果要区分这两部分,需要给直线规定方向,以及从人的角度规定左侧和右侧,这样的规定在直觉上就是给平面规定了正反面。而且在这样的规定下,其它任何有向直线的左右测也可以被唯一指出,而不会出现矛盾(不协调),请自行证明。当人“俯瞰”正平面时(直线方向和左右侧符合人体方向),逆时针描述的面积度量\(s=[ABC]\)(内点在有向线段\(AB,BC,CA\)左侧),称为正周向面积度量,反之\(-s=[ACB]\)称为负周向面积度量。
下面看有向面积度量的性质。首先如下左图,根据乘积的定义和分配率有\([ABC]=[ABD]+[ADC]\),由此不难证明对\(\triangle ABC\)外任意点\(O\)(以下右图),恒有式(1)成立。我们据此来考察任意\(\triangle ABC\)分割成的小三角形的正周向面积度量之和,取多边形外一点\(O\),度量之和又被分解为若干\([OXY]\)之和。如果\(XY\)在三角形边上,它只被使用一次;而如果\(XY\)在三角形内部,它会被使用两次且一定方向相反,所以和值相互抵消。也就是说最终的面积度量之和,总还是\([ABC]\)。对于多边形的面积度量,自然是用分割后的三角形面积度量之和,如果有多种分割方法,类似剖分相等传递性的证明,也可知多边形面积度量的唯一性。

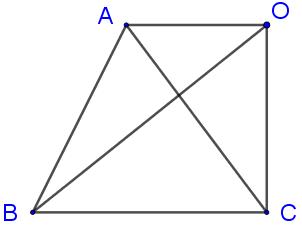
\[[ABC]=[OAB]+[OBC]+[OCA]\tag{1}\]
最后,根据多边形面积度量的唯一性,不难推断出拼补相等(包含剖分相等)的两个多边形,其面积度量也是相等的。这时回到上面的问题,两个同底\(a\)且拼补相等的三角形,由于面积度量相等\(ah/2=ah'/2\),自然得到高相等\(h=h'\)。这就是说,任何多边形对应的“股1”直角三角形(拼补相等)都是唯一的。如果两个多边形的面积度量相等,它们对应的“股1”直角三角形就一样,所以这两个多边形又是拼补相等的。欧几里得几何中的直观描述是:面积相等的两个多边形一定可以分成若干全等的三角形。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号