离散数学实验——关系及操作
3.1实验目的
关系是集合论中的一个十分重要的概念,关系性质的判定是集合论中的重要内容。通过该组实验,更加深刻地理解关系的概念和性质,并掌握关系性质的判定及关系的闭包的求法。
3.2实验内容
1、键盘输入集合A中的所有元素,并输入关系R中的所有序偶对,建立关系R的关系矩阵;
2、判断关系所具有的性质;
3、求关系R的逆关系,及关系的合成运算;
4、求关系R的r(R)、s(R)、t(R)。(注意关系的传递闭包采用Warshall算法)。
5、判断关系R是否为等价关系,若是等价关系,则求出其所有等价类;
6、选做:求集合A上的等价关系数
3.3主要算法思想
1、键盘输入集合A中的所有元素,并输入关系R中的所有序偶对,建立关系R的关系矩阵;
①用字符串ListA保存集合A中所有元素,每个字符就是一个元素
②然后用List_Relation保存关系R。
③然后定义一个方法建立关系R的关系矩阵。
2、判断关系所具有的性质
关系性质的充要条件:
设R为A上的关系, 则
(1)
R在A上自反当且仅当 IA⊆R
(2) R在A上反自反当且仅当 R∩IA=Ø
(3)
R在A上对称当且仅当 R=R-1
(4) R在A上反对称当且仅当 R∩R-1⊆IA
(5)
R在A上传递当且仅当 R°R⊆R
判断自反性:
①关系R是自反性说明 R包含集合A的恒等关系;
②所以根据在1建立的关系矩阵来判断,利用一层循环判断对角线的值是否为1,若对角线上的值有一个为0返回false,都为1的话最后返回true;
///判断自反性
///List_Relation是自反性说明 List_Relation包含集合A的恒等关系
///所以利用循环判断每个元素
bool ReflexivityJudge(int** R) {
for (int i = 0; i < ListA.length(); i++)
if (R[i][i] == 0)
return false;
return true;
}
判断反自反性:
①关系R是反自反性说明在关系矩阵中对角线的值都为0;
②所以还是根据在1建立的关系矩阵来判断,还是利用一层循环判断对角线的值是否为1,若对角线上的值有一个为1返回false,都为0的话最后返回true;
///判断反自反性
///R在A上反自反当且仅当 R∩IA=空集
///意思就是没有一个环
bool InverserReflexivityJudge(int** R) {
int n = ListA.length();
for (int i = 0; i < n; i++) {
if (R[i][i] == 1) return false;
}
return true;
}
判断对称性:
①关系R是对称性则说明它的关系矩阵一定是对称矩阵;
②所以利用两层循环遍历矩阵所有位置,并每次判断当前位置的值与他对称位置的值是否相等(R[i][j]==R[j][i]),若有一次不相等返回false,全部相等则返回true;
///判断对称性
///List_Relation满足对称性,则说明它的关系矩阵一定是对称矩阵
bool SymmetryJudge(int** R) {
for (int i = 0; i < ListA.length(); i++)
for (int j = 0; j < i; j++)if (R[i][j] != R[j][i])return false;
return true;
}
判断反对称性:
①R在A上反对称当且仅当 R∩R-1ÍIA,说明在关系矩阵中除了对角线外,其余位置的值和对应的对称位置的值不能相等。
②利用两层循环遍历矩阵所有位置,当有一次满足(当前位置不在对角线上&&当前位置的值与对称位置的值都为1)则返回false,若都没有满足则返回true;
///判断反对称性
/// R在A上反对称当且仅当 (R∩R的逆)包含于IA
///
bool InverseSymmtryJudge(int** R) {
for (int i = 0; i < ListA.length(); i++)
for (int j = 0; j < i; j++)if (R[i][j] == 1 && (R[i][j] == R[j][i]) && (i != j))return false;
return true;
}
判断传递性:
①R在A上传递当且仅当 R°RÍR,所以需要先求R°R后的矩阵S。
②求完合成后的矩阵S后,则利用两层循环遍历S和R两个矩阵,因为矩阵都是由0和1组成,所以判断SÍR只需要判断S的每个值是否大于对应R的值,若大于则返回false,没有大于的就返回true;
/// 判断传递性
/// R在A上传递当且仅当 (R·R)包含于R
bool TransitivityJudge(int** R) {
int n = ListA.length();
InitMatrix(S);
Synthetise(R);//求R合成R,传R进去,修改的是S
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (S[i][j] > R[i][j]) return false;
}
}
return true;
}
3、求关系的R的逆关系,及关系的合成运算
求关系R的逆关系:
①定义一个R_InverseMatrix用来保存R的逆关系矩阵,两层循环遍历R关系矩阵然后把当前位置的值赋值给R_InverseMatrix的对称位置;
合成运算:
①先两层循环遍历,R[i][j]若值为1则再增加依次循环,遍历R[k][i]。如果R[k][i]值为1则合成后的关系矩阵S[k][j]=1;
4、求关系R的r(R)、s(R)、t(R)(注意关系的传递闭包采用Warshall算法)
求自反闭包r(R):
①相当于是求R和恒等关系的并集,所以直接把矩阵对角线的值置为1就行了;
②然后再根据自反闭包矩阵来求出r(R);
对称闭包s(R):
①如果R中存在<x,y>,且没有<y,x>的,就把<y,x>添加到R中
②然后再根据对称闭包矩阵来求出s(R);
传递闭包t(R):
①用Warshall算法,考虑 n+1个矩阵的序列M0, M1, …, Mn, 将矩阵 Mk 的 i 行 j 列的元素记作Mk[i,j]. 对于k=0,1,…,n, Mk[i,j]=1当且仅当在R 的关系图中存在一条从 xi 到 xj 的路径,并且这条路径除端点外中间只经过{x1, x2, …, xk}中的顶点. 不难证明M0就是R 的关系矩阵,而 Mn 就对应了R 的传递闭包;
②Warshall算法:
输入:M (R 的关系矩阵)
输出:Mt (t(R)的关系矩阵)
1. Mt=M
2. for k=1 to n do
3. for i=1 to n do
4. for j=1 to n do
5. Mt[i, j] =Mt[i, j] + Mt[i, k]*Mt[k, j]
5、判断关系R是否为等价关系,若是等价关系,则求出其所有等价类;
判断是否为等价关系:
①若关系R同时满足自反、对称、传递则说明是等价,可以用上面2中的方法直接判断
求所有等价类:
①若有<x,y>∈R,则说明x,y都是在同一个等价类中。
6、求集合A上的等价关系数
①利用Stirling 数计算公式:
1.S(n, 0) = 0
2.S(n, 1) = 1
3.S(n, 2) = 2^(n − 1) − 1
4.S(n, n − 1) = C(n, 2)
5.S(n, n) = 1
②Stirling 数递推公式 : S(n, r) = r S(n − 1, r) + S(n − 1, r − 1),使用递归算法计算;
③最后集合A的关系数=S(n,1)+S(n,2)+.....+S(n,n);
3.4源程序及测试结果
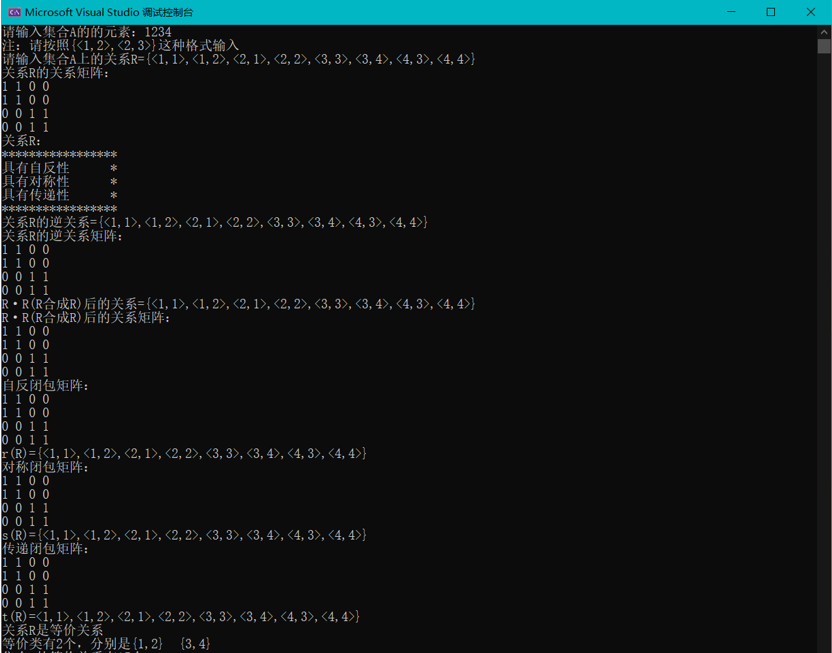

3.5完整代码
#include <iostream>
#include <string>
using namespace std;
string ListA;//定义全局集合
string List_Relation,List_InverseRelation;//定义全局集合的关系和逆关系
int** R_Matrix,**R_InverseMatrix;//R_matrix为List_Relation的关系矩阵,R_InverseMatrix为逆关系矩阵,
int** S;//R合成R后的关系矩阵
char** EC;//等价关系R的等价类
//返回字符在集合中的下标
int Get_Index(string List, char ch)
{
int i;
for (i = 0; i < List.length(); i++)if (List[i] == ch)return i;
}
//初始化矩阵
void InitMatrix(int**& M) {
int n = ListA.length();
//动态创建二维数组
M = new int* [n];
for (int i = 0; i < n; i++)
M[i] = new int[n];
//先将矩阵全置为0
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)M[i][j] = 0;
}
//输入关系并创建关系矩阵
void CreateRelation()
{
int x, y;//定义矩阵中的位置y代表行数,x代表列数
//输入关系有序偶对 请按照{<1,2>,<2,3>}输入
cout << "注:请按照{<1,2>,<2,3>}这种格式输入" << endl;
cout << "请输入集合A上的关系R=";
cin >> List_Relation;
int n = List_Relation.length();
InitMatrix(R_Matrix);//初始化矩阵
for (int i = 2; i < n; i+=6) {
y = Get_Index(ListA,List_Relation[i]);
x = Get_Index(ListA, List_Relation[i + 2]);
R_Matrix[y][x] = 1;
}
}
//根据List_Relation得到它的逆关系List_InverseRelation和逆矩阵
void GetInverseRelation() {
int n= ListA.length();
List_InverseRelation = List_Relation;
InitMatrix(R_InverseMatrix);
R_InverseMatrix = R_Matrix;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (R_Matrix[i][j] != 0)
R_InverseMatrix[j][i] = R_Matrix[i][j];
}
}
for (int i = 2; i < n; i += 6) {
char temp;
temp = List_InverseRelation[i];
List_InverseRelation[i] = List_InverseRelation[i + 2];
List_InverseRelation[i + 2] = temp;
}
}
//关系合成(只能自己合成自己)
//S是合成后的关系矩阵
void Synthetise(int **R) {
int n = ListA.length();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (R[i][j] == 1) {
for (int k = 0; k < n; k++) {
if (R[k][i] == 1) S[k][j] = 1;
}
}
}
}
}
//生成R合成R后的关系字符串
string GetSynthetiseStr(){
int n = ListA.length();
string SynthetiseStr;//R合成R后的关系字符串
SynthetiseStr = "{";
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++) {
if (S[i][j] == 1) {
SynthetiseStr = SynthetiseStr + "<" + ListA[i] + "," + ListA[j] + ">,";
}
}
}
SynthetiseStr.erase(SynthetiseStr.length() - 1, 1);
SynthetiseStr += '}';
return SynthetiseStr;
}
//输出矩阵
void MatrixOut(int **M) {
int n = ListA.length();
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << M[i][j] << " ";
}
cout << endl;
}
}
#pragma region 关系的判断
///判断自反性
///List_Relation是自反性说明 List_Relation包含集合A的恒等关系
///所以利用循环判断每个元素
bool ReflexivityJudge(int** R) {
for (int i = 0; i < ListA.length(); i++)
if (R[i][i] == 0)
return false;
return true;
}
///判断反自反性
///R在A上反自反当且仅当 R∩IA=空集
///意思就是没有一个环
bool InverserReflexivityJudge(int** R) {
int n = ListA.length();
for (int i = 0; i < n; i++) {
if (R[i][i] == 1) return false;
}
return true;
}
///判断对称性
///List_Relation满足对称性,则说明它的关系矩阵一定是对称矩阵
bool SymmetryJudge(int** R) {
for (int i = 0; i < ListA.length(); i++)
for (int j = 0; j < i; j++)if (R[i][j] != R[j][i])return false;
return true;
}
///判断反对称性
/// R在A上反对称当且仅当 (R∩R的逆)包含于IA
///
bool InverseSymmtryJudge(int** R) {
for (int i = 0; i < ListA.length(); i++)
for (int j = 0; j < i; j++)if (R[i][j] == 1 && (R[i][j] == R[j][i]) && (i != j))return false;
return true;
}
/// 判断传递性
/// R在A上传递当且仅当 (R·R)包含于R
bool TransitivityJudge(int** R) {
int n = ListA.length();
InitMatrix(S);
Synthetise(R);//求R合成R,传R进去,修改的是S
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (S[i][j] > R[i][j]) return false;
}
}
return true;
}
#pragma endregion
#pragma region 求关系的闭包
///自反闭包 相当于是求R和恒等关系的并集 直接把矩阵对角线的值置为1就行了
/// r(R)=R∪R^0
/// R^0=I(A)
void ReflexivityClosure() {
string ReflexivityStr;//用来保存自反闭包的集合字符串
int n = ListA.length();
//int** R;//自反闭包关系矩阵
//R = new int* [n];
//for (int i = 0; i < n; i++)R[i] = new int[n];
//R = R_Matrix;
ReflexivityStr = "{";
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++) {
if (i == j) {
cout << "1 ";
ReflexivityStr = ReflexivityStr + "<" + ListA[i] + "," + ListA[j] + ">,";
continue;
}
else cout << R_Matrix[i][j] << " ";
if (R_Matrix[i][j] == 1) {//矩阵中为1的才有关系,则要保存在集合字符串中
ReflexivityStr = ReflexivityStr + "<" + ListA[i] + "," + ListA[j] + ">,";
}
}
cout << endl;
}
ReflexivityStr.erase(ReflexivityStr.length()-1,1);
ReflexivityStr += '}';
cout << "r(R)="<<ReflexivityStr;
}
///对称闭包
/// 如果有<x,y>且没有<y,x> 则添加<y,x>到集合中
/// s(R)=R∪R^-1
void SymmtryClosure() {
string SymmtryStr;//用来保存对称闭包的集合字符串
int n = ListA.length();
int** R;//对称闭包关系矩阵
R = new int* [n];
for (int i = 0; i < n; i++)R[i] = new int[n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
R[i][j] = R_Matrix[i][j];
SymmtryStr = "{";
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
//关系中如果有<x,y>且没有<y,x> 则添加<y,x>到集合中
if (R[i][j] == 1 && R[j][i] != 1) {
R[j][i] = 1;
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << R[i][j] << " ";
if (R[i][j] == 1)
{
SymmtryStr = SymmtryStr + "<" + ListA[i] + "," + ListA[j] + ">,";
}
}
cout << endl;
}
SymmtryStr.erase(SymmtryStr.length() - 1, 1);
SymmtryStr += '}';
cout << "s(R)=" << SymmtryStr;
}
///传递闭包(采用Warshall算法)
/// t(R)=R∪R^2∪R^3∪…
void TransitivityClosure() {
string TransitivityStr;//用来保存对称闭包的集合字符串
int n = ListA.length();
int** R;//对称闭包关系矩阵
R = new int* [n];
for (int i = 0; i < n; i++)R[i] = new int[n];
for (int i = 0; i < n; i++)
for(int j=0;j<n;j++)
R[i][j] = R_Matrix[i][j];
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (R[j][i]==1)
{
for (int k = 0; k < n; k++)
{
R[j][k] = R[j][k] | R[i][k];//逻辑加
}
}
}
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << R[i][j] << " ";
if (R[i][j] == 1)
{
TransitivityStr = TransitivityStr + "<" + ListA[i] + "," + ListA[j] + ">,";
}
}
cout << endl;
}
TransitivityStr.erase(TransitivityStr.length() - 1, 1);
TransitivityStr += '}';
cout << "t(R)=" << TransitivityStr;
}
#pragma endregion
///判断关系R是否为等价关系
/// 如果R同时满足自反、对称、传递则是等价
bool EqualJudge(int **R) {
if (ReflexivityJudge(R_Matrix) && SymmetryJudge(R_Matrix) && TransitivityJudge(R_Matrix))
return true;
else
return false;
}
/// 求出所有等价类
/// 如果<x,y>∈R,则说明x,y在同一个等价类
/// 例如:等价关系R={<1,2><2,1><1,3><3,1><2,3><3,2><4,5><5,4>}∪IA
/// 则等价类有两个{1,2,3},{4,5}
void GetEqualClass(int **R) {
int n = ListA.length();
string A = ListA;
EC = new char*[n];//最大的等价类个数就是元素个数
int Num=0;//等价类个数
int ip;
for (int i = 0; i < n; i++) {
if (A[i]) {
ip = 0;
EC[Num] = new char[n];
EC[Num][ip++] = A[i];
for (int j = i + 1; j < n; j++) {
if (A[i] && R[i][j]) {
EC[Num][ip++] = A[j];
A[j] = 0;
}
}
EC[Num][ip] = '\0';
Num++;
}
}
cout << "等价类有" << Num << "个,分别是";
for (int i = 0; i < Num; i++) {
cout << "{";
for (int j = 0; j < strlen(EC[i]); j++) {
if (j == strlen(EC[i]) - 1)
cout << EC[i][j];
else
cout << EC[i][j] << ",";
}
cout << "} ";
}
}
//计算组合n是下指数,m是上指数
int C(int n, int m) {
int N_Fact = 1;//n的阶乘
int M_Fact = 1;//m的阶乘
int NSM_Fact = 1;//n-m的阶乘
for (int i = 1; i <= n; i++)
N_Fact *= i;
for (int i = 1; i <= m; i++)
M_Fact *= i;
for (int i = 1; i <= n - m; i++)
NSM_Fact *= i;
return N_Fact / (NSM_Fact * M_Fact);
}
///第二类 Stirling 数计算方法
/// 1.Stirling 数计算公式 :
//① S(n, 0) = 0
//② S(n, 1) = 1
//③ S(n, 2) = 2^(n − 1) − 1
//④ S(n, n − 1) = C(n, 2)
//⑤ S(n, n) = 1
//2.Stirling 数递推公式 : S(n, r) = r S(n − 1, r) + S(n − 1, r − 1)
int Stirling(int n, int m) {
if (m == 0)
return 0;
else if (m == 1)
return 1;
else if (m == 2)
return pow(2, n - 1) - 1;
else if (m == n - 1)
return C(n, 2);
else if (n == m)
return 1;
else
{
return m * Stirling(n - 1, m) + Stirling(n - 1, m - 1);
}
}
/// 求出等价关系数
/// 算等价关系数相当于是算有多少种组合,又因为集合A的等价关系与划分个数是一一对应的,因此求其划分个数即可
/// 在有n个元素的集合里面,有1个元素的划分、2个元素的划分.....到n个元素的划分
/// 最后再把所有划分的个数加起来
/// 等价关系数=S(n,1)+S(n,2)+.....+S(n,n)
void GetEqualClassNum() {
int allNum=0;
int n = ListA.length();
for (int i = 1; i <= n; i++)
allNum += Stirling(n, i);
cout << "集合A的等价关系有" << allNum << "个;";
}
//创建集合
void ListCreat() {
while (true)
{
cout << "请输入集合A的的元素:";
cin >> ListA;
bool flag;
for (int j = 0; j < ListA.length(); j++) {
flag = true;
for (int k = j + 1; k < ListA.length(); k++) {
if (ListA[j] == ListA[k])
{
flag = false;
break;
}
}
if (!flag)
break;
}
if (!flag) {
cout << "集合中不允许存在相同元素!,请重新输入!" << endl;;
}
else
{
break;
}
}
}
void main() {
//1、键盘输入集合A中的所有元素,并输入关系R中的所有序偶对,建立关系R的关系矩阵
cout << "1、键盘输入集合A中的所有元素,并输入关系R中的所有序偶对,建立关系R的关系矩阵;" << endl;
ListCreat();
CreateRelation();
cout << "关系R的关系矩阵:" << endl;
MatrixOut(R_Matrix);
//2、判断关系所具有的性质
cout << endl << "2、判断关系所具有的性质" << endl;
cout << "关系R:" << endl;
cout << "*****************\n";
if (ReflexivityJudge(R_Matrix))
cout << "具有自反性\t*" << endl;
if(InverserReflexivityJudge(R_Matrix))
cout << "具有反自反性\t*" << endl;
if (SymmetryJudge(R_Matrix))
cout << "具有对称性\t*" << endl;
if (InverseSymmtryJudge(R_Matrix))
cout << "具有反对称性\t*" << endl;
if (TransitivityJudge(R_Matrix))
cout << "具有传递性\t*" << endl;
cout << "*****************\n";
//3、求关系R的逆关系,及关系的合成运算;
cout << endl << "3、求关系R的逆关系,及关系的合成运算" << endl;
GetInverseRelation();
cout << "关系R的逆关系=" << List_InverseRelation << endl;
cout << "关系R的逆关系矩阵:" << endl;
MatrixOut(R_InverseMatrix);
cout << "R·R(R合成R)后的关系=" << GetSynthetiseStr() << endl;
cout << "R·R(R合成R)后的关系矩阵:" << endl;
MatrixOut(S);
//4、求关系R的r(R)、s(R)、t(R)
cout << endl << "4、求关系R的r(R)、s(R)、t(R)" << endl;
cout << "自反闭包矩阵:" << endl;
ReflexivityClosure();
cout << endl;
cout << "对称闭包矩阵:" << endl;
SymmtryClosure();
cout << endl;
cout << "传递闭包矩阵:" << endl;
TransitivityClosure();
cout << endl;
//5、判断关系R是否为等价关系,若是等价关系,则求出其所有等价类
cout <<endl<< "5、判断关系R是否为等价关系,若是等价关系,则求出其所有等价类" << endl;
cout << "关系R";
if (EqualJudge(R_Matrix)) {
cout << "是等价关系\n";
GetEqualClass(R_Matrix);
}
else
cout << "不是等价关系";
cout << endl;
//6.求集合A上的等价关系数
cout << endl << "6.求集合A上的等价关系数" << endl;
GetEqualClassNum();
}
①关系R是自反性说明 R包含集合A的恒等关系;
②所以根据在1建立的关系矩阵来判断,利用一层循环判断对角线的值是否为1,若对角线上的值有一个为0返回false,都为1的话最后返回true;
判断反自反性:
①关系R是反自反性说明在关系矩阵中对角线的值都为0;
②所以还是根据在1建立的关系矩阵来判断,还是利用一层循环判断对角线的值是否为1,若对角线上的值有一个为1返回false,都为0的话最后返回true;
判断对称性:
①关系R是对称性则说明它的关系矩阵一定是对称矩阵;
②所以利用两层循环遍历矩阵所有位置,并每次判断当前位置的值与他对称位置的值是否相等(R[i][j]==R[j][i]),若有一次不相等返回false,全部相等则返回true;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号