相机对焦中前后景深和光圈关系计算

笔者在查询景深计算时，发现网上主流的光学模型为以下两种，而很少有写景深公式如何计算，因此本文来探讨下如何计算景深。

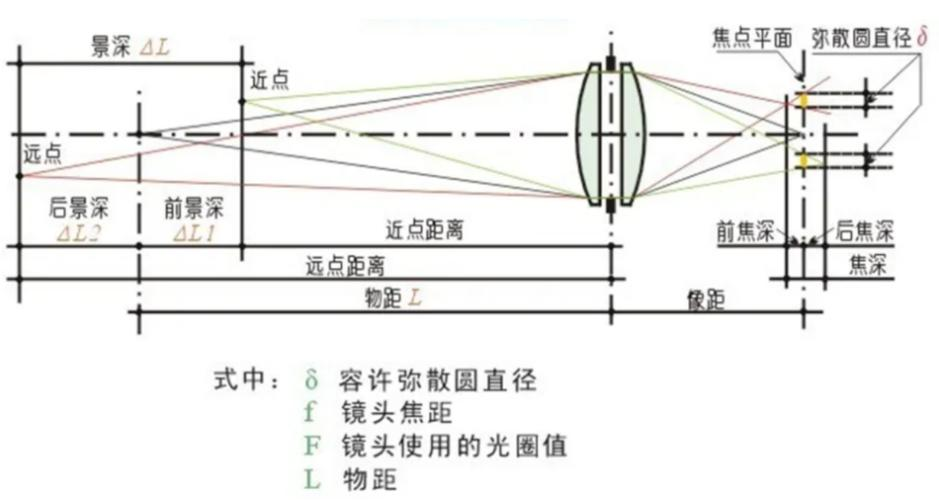
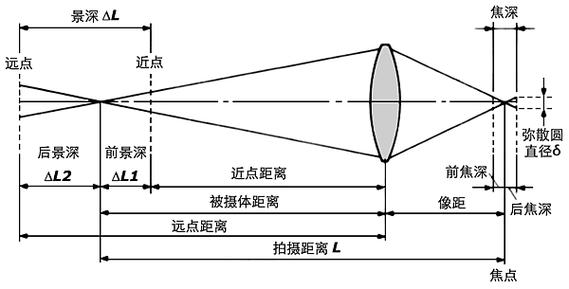
相信聪明的读者已经发现上面两个的区别了，就是弥散圆的定义。如果光线没有汇聚在焦平面，那么在焦平面上会形成圆形光斑，而肉眼分辨率下能容许的光斑直径就是弥散圆直径。当物体或背景超出景深时，在焦平面上的弥散圆直径就会超过容许范围，视觉上就会有虚化的效果。从这个角度看，第一个模型更符合弥散圆直径的定义，因此本文用第一个模型来计算。

我们在第一张图的基础上定义符号：

符号	说明
\(f\)	镜头焦距
\(L\)	物距
\(u\)	相距
\(\delta\)	容许弥散圆直径
\(D\)	镜头直径
\(F\)	光圈，定义为焦距和镜头直径之比
\(\Delta L1,\Delta L2\)	前、后景深
\(\Delta u1,\Delta u2\)	前、后焦深

由定义有

\[F=f/D \]

由成像公式有

\[\frac1f = \frac1L + \frac1u \]

我们先计算前景深，其成像位置对应后焦深，由比例关系可得

\[\begin{aligned} \frac{\delta}D&=\frac{\Delta u2}{u+\Delta u2} \\ u &= \frac{fL}{L-f} \\ \Delta u2 &= \frac{fFL\delta}{(L-f)(f-F\delta)} \end{aligned} \]

于是由成像公式有

\[\begin{aligned} \frac1f &= \frac1{L-\Delta L1} + \frac1{u+\Delta u2} \\ \frac1f &= \frac{Lf-f^2-LF\delta+fF\delta}{f^2L} + \frac1{L-\Delta L1} \\ \frac1{L-\Delta L1} &= \frac{f^2+LF\delta-fF\delta}{f^2L} \\ \Delta L1 &= \frac{L^2F\delta-fFL\delta}{f^2+LF\delta-fF\delta} \\ &=\frac{LF\delta(L-f)}{f^2+F\delta(L-f)} \end{aligned} \]

同样也可得

\[\Delta L2=\frac{LF\delta(L-f)}{f^2-F\delta(L-f)} \]

在一般摄影环境中有\(L>>f\)，于是化简得

\[\begin{aligned} \Delta L1 &=\frac{L^2F\delta}{f^2+LF\delta} \\ \Delta L2 &=\frac{L^2F\delta}{f^2-LF\delta} \end{aligned} \]