machine learning 之 Recommender Systems

整理自Andrew Ng的machine learning 课程 week 9.

 

目录：

• Problem Formulation（问题的形式）
• Content Based Recommendations（基于内容的推荐）
• Collaborative Filtering（协同过滤）
• Collaborative Filtering Algorithm（协同过滤算法）
• Vectorization: Low Rank Matrix Factorization（向量化：矩阵低秩分解）
• Implementation Detail: Mean Normalization（具体实施：均值正则化）

 

1、Problem Formulation

推荐系统在机器学习领域是一个很流行的应用。

比如说，我们尝试向用户推荐电影。我们可以使用以下定义：

• $n_u$：the number of users，用户数
• $n_m$：the number of movies，电影数
• $r(i,j)=1$ if user j has rated movie i，用户j是否对电影i进行了评分
• $y(i,j)$：rating given by user j to movie i（只有在r(i,j)=1时才有值），用户j对电影i的评分

 

2、Content Based Recommendations

我们可以定义两个特征$x_1$和$x_2$，分别代表电影的浪漫程度和动作程度（值在0-1之间）；

一个预测电影评分的做法可以是，对每一个用户做linear regression，得到每个用户的$\theta^{(j)} \in R^3$（这里自动加入了$x_0=1$），这样对用户j对电影i的评分的预测值就是$(\theta^{(j)})^Tx^{(i)}$；

• $\theta^{(j)}$：用户j的参数向量
• $x^{(i)}$：电影i的特征向量

对于用户j，电影i，预测的评分即为$(\theta^{(j)})^Tx^{(i)}$

• $m^{(j)}$：用户j打分的电影数目

为了学习参数向量$\theta^{(j)}$（用户j的参数向量），我们作如下操作：

$min_{\theta^{(j)}} \quad \frac{1}{2} \sum_{i:r(i,j)=1}{(\theta^{(j)}x^{(i)}-y^{(i,j)})}^2+\frac{\lambda}{2}\sum_{k=1}^{n}{(\theta_k^{(j)})}^2$

这其实是和线性回归的类似的损失函数

为了学习所有用户的参数向量：

$min_{\theta^{(1)},...,\theta^{(n_u)}} \quad \frac{1}{2} \sum_{j=1}^{n_u} \sum_{i:r(i,j)=1}{(\theta^{(j)}x^{(i)}-y^{(i,j)})}^2+\frac{\lambda}{2} \sum_{j=1}^{n_u} \sum_{k=1}^{n}{(\theta_k^{(j)})}^2$

以上的损失函数和线性回归中的损失函数一样，所以我们也可以用线性回归的梯度下降法去更新参数：

$\theta_k^{(j)} = \theta_k^{(j)} - \alpha \sum_{i:r(i,j)=1}  ((\theta^(j))^Tx^{(i)} - y^{(i,j)}) x_k^{(i)} \quad k=0$

$\theta_k^{(j)} = \theta_k^{(j)} - \alpha (\sum_{i:r(i,j)=1} ((\theta^(j))^Tx^{(i)} - y^{(i,j)}) x_k^{(i)} + \lambda \theta_k^{(j)}) \quad k \neq 0$

这里唯一与线性回归中的不同就是省略掉的常数m是不一样的。

 

3、Collaborative Filtering

实际中很难去定义和计算一部电影的浪漫度和动作度，为了解决这个问题，可以使用feature finder；

可以在之前询问用户对不同种类的电影的喜爱程度，直接提供$\theta$参数；

然后就可以通过参数推算特征了：

$min_{x^{(1)},...,x^{(n_m)}}  \quad \frac{1}{2} \sum_{i=1}^{n_m} \sum_{j:r(i,j)=1}{(\theta^{(j)}x^{(i)}-y^{(i,j)})}^2+\frac{\lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^{n}{(x_k^{(i)})}^2$

 

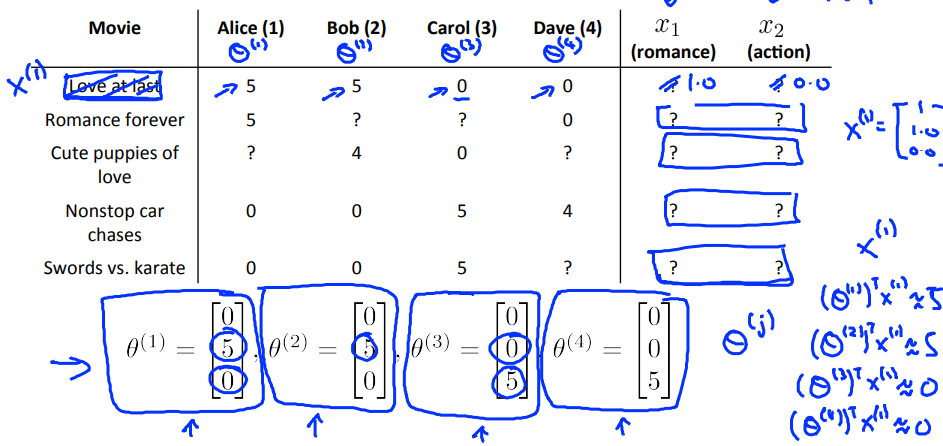
你也可以随机的猜测一些$\theta$的值，然后用这些$\theta$的值去计算特征的值，这样重复的计算，最后也可以收敛到比较好的特征的值

 依据上述：

• 知道了参数$\theta$，我们可以估计特征x；
• 知道了特征x，我们可以估计参数$\theta$；

这就是协同过滤（Collaborative Filtering）。

 

4、Collaborative Filtering Algorithm

为了加快计算的速度，我们其实可以在最小化时同步的计算参数和特征：

$J(x,\theta) = \frac{1}{2} \sum_{(i,j):r(i,j)=1} {((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})}^2 + \frac{lambda}{2} \sum_{j=1}^{n_u} \sum_{k=1}^{n}{(\theta_k^{(j)})}^2 + \frac{lambda}{2} \sum_{i=1}^{n_m} \sum_{k=1}^n {(x^{(i)})}^2$

这个式子看起来比较复杂，其实只是结合了参数$\theta$和特征x的损失函数，由于算法可以学习，所以不需要设定一个$x_0=1$，因此$x \in R^n, \theta \in R^n$；

完整算法如下：

1. 将$x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)}$初始化为一些随机的很小的值；（不能把它们初始化为0，因为和神经网络中一样，要break symmetry，否则计算出来的特征的值都是一样的）
2. 使用梯度下降（或者其他的优化算法）最小化$J(x^{(1)},...,x^{(n_m)},\theta^{(1)},...,\theta^{(n_u)})$，参数的更新如下：

• • $x_k^{(i)} = x_k^{(i)} - \alpha{(\sum_{j:r(i,j)=1} {({(\theta^{(j)})}^Tx^{(i)}- y^{(i,j)})\theta_k^{(j)}} + \lambdax_k^{(i)})}$
  • $\theta_k^{(j)} = \theta_k^{(j)} - \alpha{(\sum_{i:r(i,j)=1} {({(\theta^{(j)})}^Tx^{(i)}- y^{(i,j)})x_k^{(i)}} + \lambda\theta_k^{(j)})}$

　　 3. 对于一个参数为$\theta$的用户和特征为x的电影，那么预测的评分为$(\theta)^Tx$

 

5、Vectorization: Low Rank Matrix Factorization

为了实现向量化的计算，公式如下：$Y=X\Theta^T$

一个m*n的矩阵的秩r如果很低，那么这个矩阵可以分解为一个m*r和一个r*n的矩阵相乘（有点类似SVD分解），所以Y可以直接分解得到X和$\Theta$

如何定义电影i和电影j的相关度？

$||x_i-x_j||$，这个值越小，说明电影i和电影j的相似度越大。

 

6、Implementation Detail: Mean Normalization

考虑一个问题，如果一个用户没有给任何一部电影评分，那么通过之前的方法计算出来的此用户对任何一部电影的评分都会是0，这显然是不对的，那么如何解决这个问题呢？

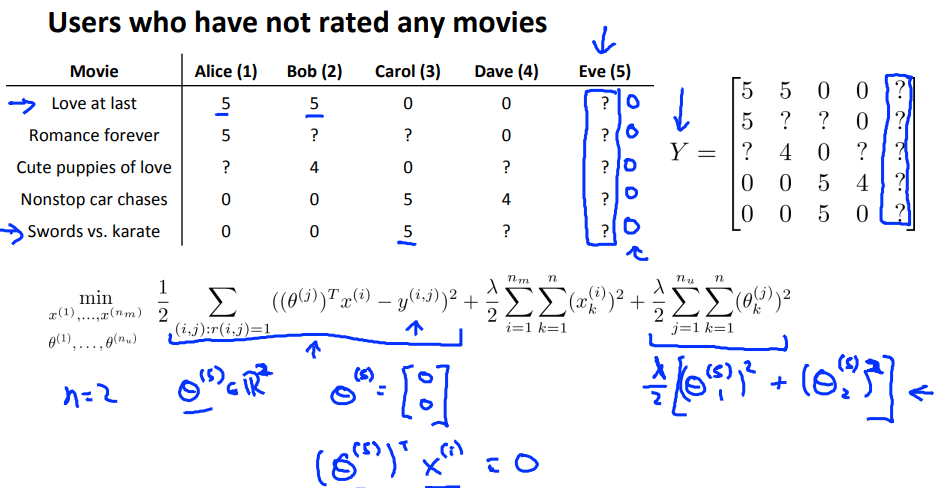
实际上，我们可以通过Mean Normalization去处理评分矩阵，得到一个新的评分矩阵$Y’=Y-\mu$，对这个新的矩阵利用协同过滤算法，计算出用户参数矩阵和特征矩阵，再进行预测评分，此时预测时需要在结果上再加上一个均值，因为我们的评分矩阵是经过处理的，所以求预测时，也需要再把这个之前减去的均值再加回来。