数据结构------数、二叉树、二叉排序树、

树

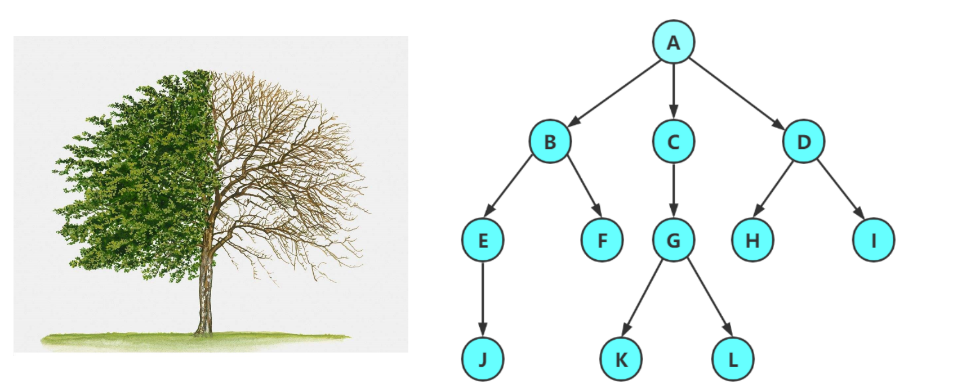
1. 树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因 为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
2. 二叉树（Binary Tree） 是数据结构领域的一颗明珠，它像自然界中的树枝分叉，又像人类社会的族谱图，用简单的规则构建出无限可能。每个节点最多有两个子节点（左孩子和右孩子），这种二分思想在算法中展现出惊人的效率。

3. 核心性质：

   • 每个节点最多有两个子节点，（左子节点和右子节点）。

   • 左子树和右子树是有序的（二叉搜索树特性）

   • 第i层最多有 2i−12i−1 个节点

   • 深度为k的树最多有 2k−12k−1 个节点

4. 前序遍历（Preorder）

   • 访问顺序：根节点 → 左子树 → 右子树

5. 中序遍历（Inorder）
   • 访问顺序：左子树 → 根节点 → 右子树
   • 应用场景：二叉搜索树排序输出
6. 后序遍历（Postorder）

• • 访问顺序：左子树 → 右子树 → 根节点
  • 应用场景：表达式求值、内存释放

 二叉查找树的递归  最近有点忙，先写这么多，待补全

/*************************************************************************
*   file name:binarysearchtree
*   function:  实现对二叉查找树的增删改查功能
*   date: 2025.5.19
*   note:none
*    Copyright (c) 2024-2025 l550036303@163.com All right reserved
**************************************************************************/

#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>

typedef int typedata_t;

typedef struct binarysearchtree{

    typedata_t keyvalue;                  //存储的数据

    struct binarysearchtree * lchild;          //结点的左孩子
    
    struct binarysearchtree * rchild;          //结点的右孩子
}BSt_t;    //binary search tree 二叉查找树

BSt_t * BSt_t_creatroot(typedata_t keyvalue){

    BSt_t * root = (BSt_t *)calloc(1,sizeof(BSt_t));

    root->keyvalue = keyvalue;

    root->lchild = NULL;

    root->rchild = NULL;

    return root;
}

BSt_t * BSt_t_creatnewnode(typedata_t keyvalue){

    BSt_t * treenew = (BSt_t *)calloc(1,sizeof(BSt_t));
    if(NULL == treenew){
        perror("creat fail\n");
        exit(-1);
    }
    treenew->keyvalue = keyvalue;

    treenew->lchild = NULL;

    treenew->rchild = NULL;

    return treenew;
}

//用 while 来遍历插入数组
bool BSt_t_InsertNode(BSt_t * root,typedata_t keyvalue){
        BSt_t * treenew = BSt_t_creatnewnode(keyvalue);
        BSt_t * temp = root;
        if(root == NULL){
            printf("add fill ,this tree is empty\n");
            return false;
        }
        
        while(temp){
                    //树中已经有该值了
                if( root -> keyvalue == keyvalue){
                    printf("this value is repeat\n");
                    return false;
                }else if( keyvalue < temp->keyvalue ){
                    if(temp->lchild == NULL){
                        temp->lchild = treenew;
                        break;
                    }
                  temp = temp->lchild;
                }else{
                    if(temp->rchild == NULL){
                        temp->rchild = treenew;
                        break;
                    }
                  temp = temp->rchild;
                }
        }

    return true;
}

//递归函数
bool BSt_t_recursion(BSt_t * node,BSt_t * new,typedata_t keyvalue){
        if(node){
            if(node->keyvalue == keyvalue){
                printf("this value is repeat\n");
                return false;
            }else if(node->keyvalue < keyvalue){
                if(node->rchild == NULL){
                    node->rchild = new;
                    return true;
                }
                BSt_t_recursion(node->rchild,new,keyvalue);
            }else{
                if(node->lchild == NULL){
                    node->lchild = new;
                    return true;
                }
                BSt_t_recursion(node->lchild,new,keyvalue);
            }
        }
        //if下来都不符合，则此次递归就自然结束
        return false;
    }
//  递归遍历
bool BSt_t_recursionInsertNode(BSt_t * root,typedata_t keyvalue){
        BSt_t * treenew = BSt_t_creatnewnode(keyvalue);
        if(root == NULL){
            printf("add fill ,this tree is empty\n");
            return false;
        }
        BSt_t_recursion(root,treenew,keyvalue);
       return true;
}




// 前序遍历（递归）
bool BSt_t_print(BSt_t * root){
    
    BSt_t * temp = root;

    if(!temp){
      return false;
    }
    else{

        printf("\t%d\t",temp->keyvalue);

        if(NULL !=temp->lchild){
            BSt_t_print(temp->lchild);
        }
        if(NULL !=temp->rchild){
            BSt_t_print(temp->rchild);
        }
    }
    return true;
}


void main(){
    BSt_t * root = BSt_t_creatroot(20);
    // BSt_t_InsertNode(root,10);
    BSt_t_recursionInsertNode(root,10);
    // BSt_t_InsertNode(root,5);
    BSt_t_recursionInsertNode(root,5);
    // BSt_t_InsertNode(root,25);
    BSt_t_recursionInsertNode(root,25);
    BSt_t_print(root);
}