Princeton Algorithms, Part I week3 Quick Sort

Quick Sort

quick sort

今天学习quick sort，quick sort的基本思想是有一个数组，先shuffle以后，保证数组的item位置是均匀分布的，选择一个item然后，把所有比这个item大的放在item右边，所有比这个item小的放在左右，然后递归的进行这个操作，如下图所示

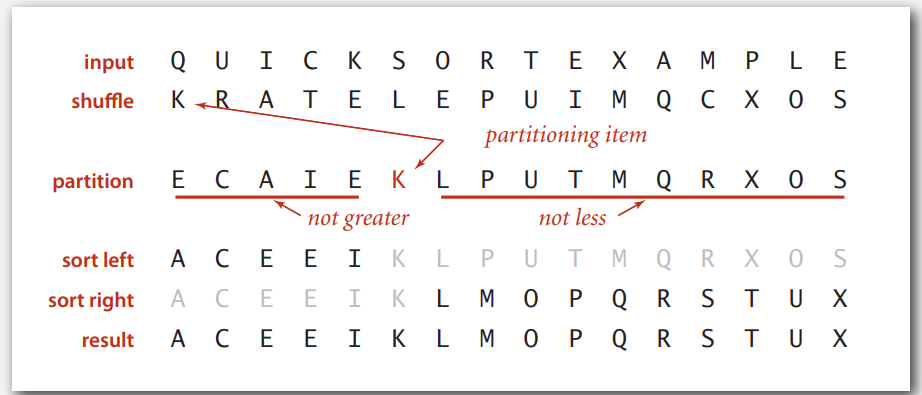
 这里面的partition部分如何实现呢？首先定义两个指针i和j ，i = lo +1，j = hi，然后i从左到右的扫描数组如果less（a[i],a[lo]）, j从右到左的扫描数组如果less（a[lo],a[j]）, 然后交换a[i]和a[j]，重复这个过程直到指针i和指针j交叉。下面是partition方法的java implementation

public class QuickSort{

   private static int partition(Comparable[] a, int lo, int hi){

                 int i = lo, j = hi + 1;
                 while(True){

                        while(less(a[++i], a[lo])){
                                if(i == hi)break;
                                
}
                         while(less(a[lo],a[--j])){
                                     if(j == lo)break;
}
                         if(i >= j) break;
                         exch(a, i, j); 


}
                         exch(a, lo, j);
                         return j;

}



}

下图是整个partition过程

 接下来是quick sort的完整的java implementation

public class QuickSort{

            public static void sort(Comparable[] a){

                        shuffle(a)； //  这里是为了让数组的item是均匀分布，是为了保证quick 
                                       //  sort的性能
                         sort(a, 0, a.length-1);

}
            private static void sort(Comparable[] a, int lo, int hi){

                     if(hi <= lo){return;}
                     int j = partition(a, lo, hi);
                     sort(a, lo, j-1);
                     sort(a, j+1, hi);
}

}

quick sort是in place的，他不需要额外的空间。在最好的情况下 quick sort的比较次数是正比于$NlgN$, 而在最坏的情况下是正比于$N^2$的.

 

我们可以分析一下在平均情况下的性能，下面是一个简单的证明过程。

 

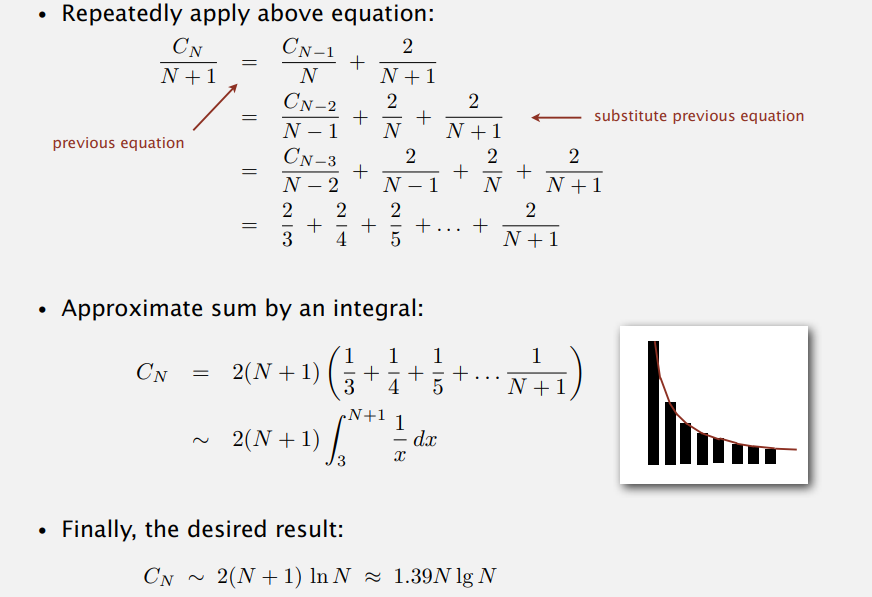
 在实际使用的时候，quick sort是非常有用的，因为比较次数是二次幂的情况是非常罕见的，它比merge sort要多大约百分之39的比较次数，但是在实际中quick sort要更快， 因为少了数据的移动。shuffle操作可以防止最坏的例子，但是如果当我们要排序的item的key是正序或者逆序或者是有很多相同的key，quick sort的性能也会很差，还有值得一提的是，quick sort 不是 stable的。在实际的使用中，对于小的数组我们可以使用insertion sort替代quick sort。

selection

让我们考虑一个问题，如何在一个N个元素的数字中，找出第k小的元素。

第一种方法是直接用排序算法排序以后，直接选出第k个，那么这是最好的解决办法了吗，和排序一样吗？

这里介绍一种平均情况下是线性运行时间的quick-selection 算法，其思想借鉴了quick sort，其java implementation和原理如下图所示。

 quick-select的平均算法性能分析类似于quick sort，最后可以得到如下的结果

 duplicate keys

有时候我们在排序的时候可能会遇到数组很大，但是里面被排序的key相同的有很多，这个时候quick sort性能表现就会比较差， merge sort表现就会比较好，但是merge sort会消耗很多额外空间。

我们希望的是当所有的key相等的时候我们就不再反复访问数组，这里提供一种方法能够当重复的key很多的时候能够保证性能的算法，如下图所示

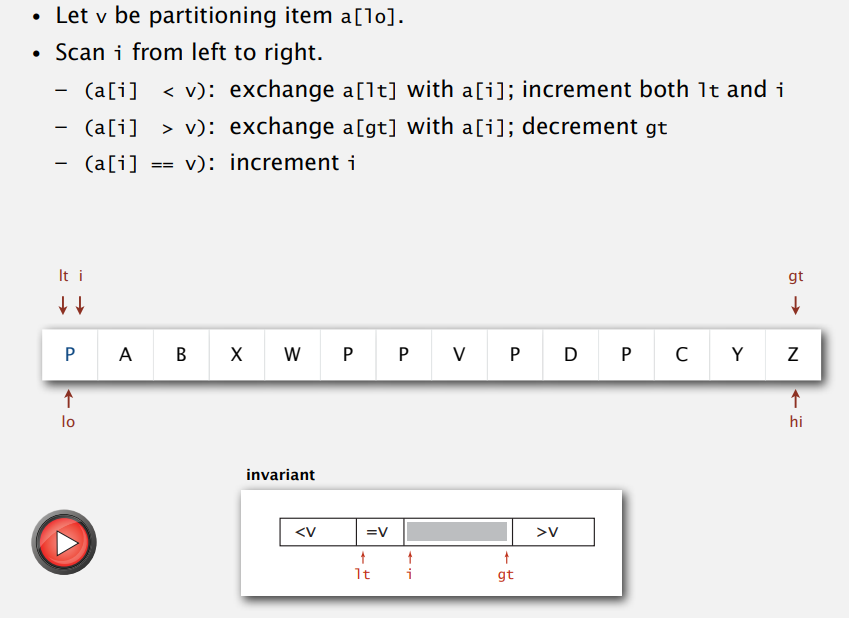
 这里面有三个指针，lt, i, gt ，i和lt都指向lo，gt指向hi。我们选择lo处的元素作为分区元素 ，然后i从左到右的访问数组，如果a[i] 小于分区元素的话，交换a[lt]和a[i]，并且 同时增加lt和i；如果a[i]大于分区元素，交换a[i]和a[gt]，同时减下gt，如果a[i]等于分区元素，那么只增加i。下面是java implementation

  private static void sort(Comparable[] a , int lo, int hi){

          if(hi <= lo) return;
          int i = lo,  lt = lo, gt = hi;
          Comparable v = a[lo];
          while(i <= gt){
               int cmp = a[i].compareTo(v);
               if(cmp < 0){exch(a, i++,lt++);}
               else if (cmp > 0){exch(a, i, gt--);}
               else{i++;}


}
           sort(a, lo, lt-1);
           sort(a, gt+1, hi);




}

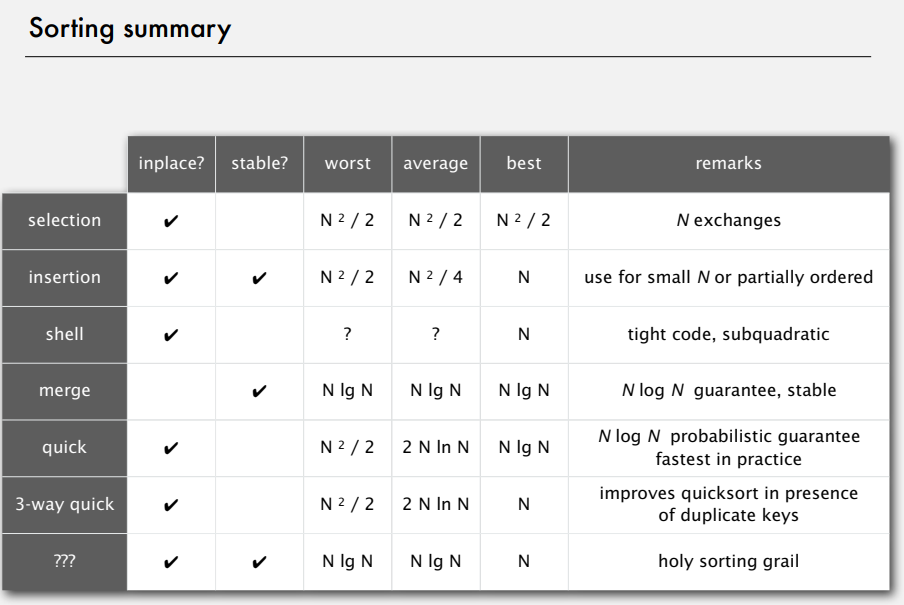
这就是今天的排序算法的学习内容，最后附上一些排序算法的总结