Princeton Algorithms, Part I week2 Elementary Sorts

Elementary Sorts

 排序算法非常重要，它的应用也特别多，这一节我们学习排序算法。

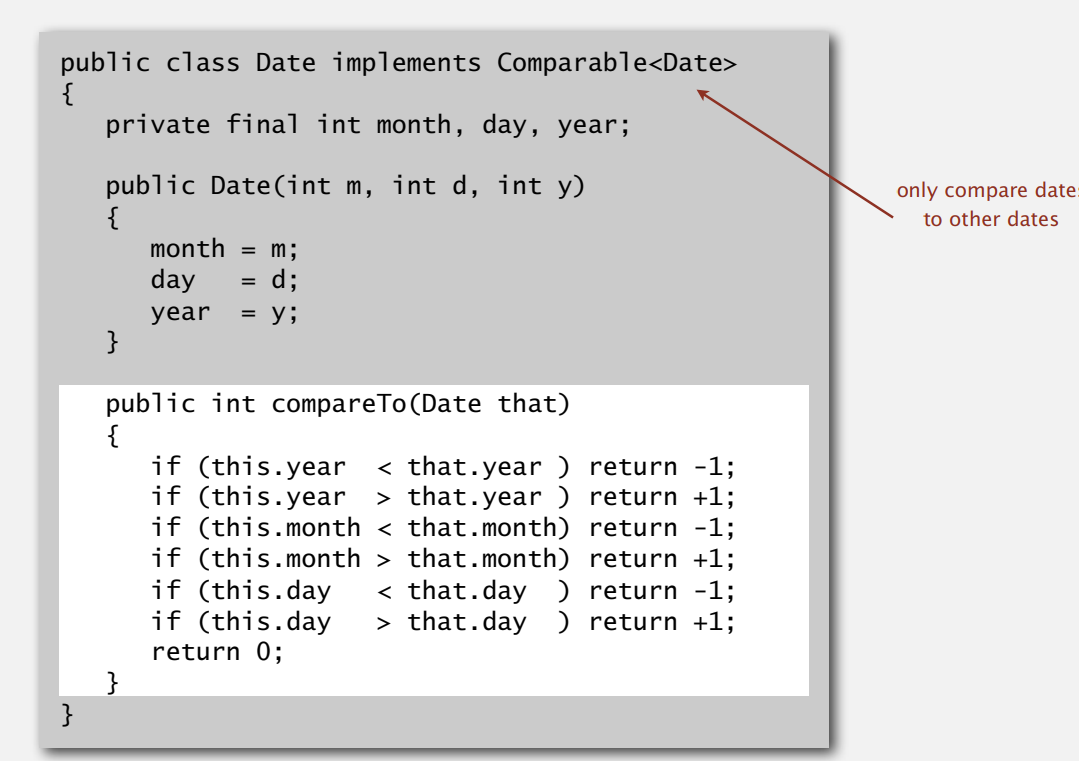
在java中，我们对需要排序的数据我们会实现Comparable接口，实现compareTo方法，大于返回1，相等返回0，小于返回-1，例如Date类

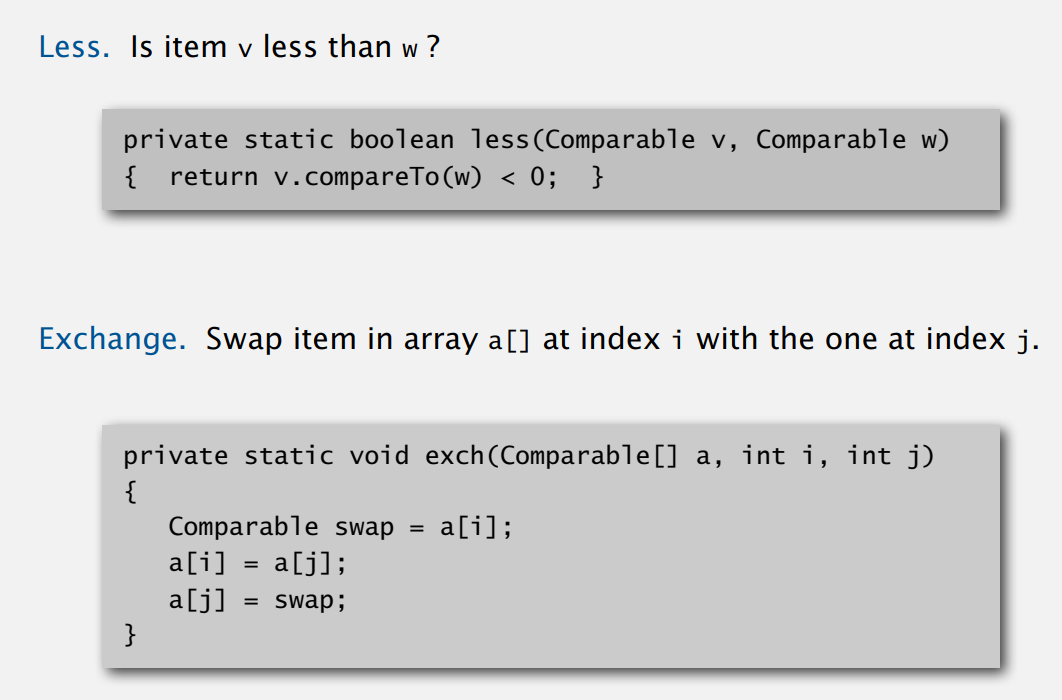
然后我们这里引入三个工具函数less，exch和isSorted，less函数主要是拿来判断是否小于，exch拿来交换数据的位置，帮助排序的时候交换位置，isSorted拿来判断是否有序。

 

 

首先我们学习selection sort

排序方法的思想非常朴素，从左到右的扫描整个数组，然后每次把最小的排到前面去。比一个长度为10的数组，index是从0到9，然后从左到右的扫描，先选定index为0的标记为min，然后从1开始扫描到9，一旦碰到比index的key小的直接就swap，然后第一轮完了以后，最小的item就到了index为0的地方，再把min设置为index为1，扫描2到9，重复整个过程。这样相当于每次都会把整个数组中未有序的部分选一个最小的拿到前面去。下面是java implementation

 

 1 public class SelectionSort{
 2             public static void sort(Comparable[] a){
 3                       int N = a.length;
 4                       for(int i = 0;i < N;i++){
 5                            int min = i;
 6                            for (int j = i+1;j< N;j++){
 7              
 8                                 if(less(a[j],a[min])){min = j;}
 9                                    }
10                            exch(a,i,min); 
11                             
12                                                 
13       }
14  } 
15 }

显然这个算法的时间复杂度是$O（N^2）$

 

接下来学习insertion sort

这个排序方法的思想是从左到右的扫描，然后在第i次迭代的时候，让a[i]与左边的item相比，如果小就直接交换，一直交换到不能交换为止，而a[i]的右边不用动。java implementation 如下

 

 1 public class InsertionSort{
 2 
 3         public void sort(Comparable a[]){
 4 
 5                   int N = a.length;
 6                   for(int i = 0;i < N;i++){
 7                          for(int j = i;j>0;j--){
 8                              if(less(a[j], a[j-1])){   exch(a,j,j-1);}
 9                              else{break;}
10                     
11                     }
12 
13             }
14 
15 
16        }
17 
18 
19 }

这个算法的时间复杂度也是$O(N^2)$.

对于部门有序的数据，可以选择这个算法。

 

接下来介绍shell sort

这个算法的思想就是，我们先部分排序，比如我们一共有12个item需要排序，然后每次间隔4个排序，然后每次间隔2个排序，最后间隔1个（也就是insertion sort），那么在实际使用中我们该如何选择这个间隔数量的序列呢？比较好的是 用3x+1的这个序列，其java implementation如下

 1 public class ShellSort{
 2 
 3         public void sort(Comparable a[]){
 4                   
 5                   int N = a.length;
 6                   int h = 1;
 7                   while(h < N/3){
 8                      h = h*3+1;
 9                }
10                  while(h>=1){
11 
12                    for(int i = h;i < N;i++){
13 
14                      for(int j = i;j>=h&&less(a[j],a[j-h]);j-=h){
15                             exch(a,j,j-h)
16 
17                       }
18 
19                         }
20                          h /=3;
21                 }
22 
23         }
24 
25 
26 }

 

实际上shell sort也就是insertion sort 的变式。

shell sort最坏的时间复杂度是$O(N^{3/2})$.

 

posted @ 2023-11-06 20:14  gauss_j  阅读(19)  评论(0)    收藏  举报