Princeton Algorithms, Part I week1 union&find

union & find

 

首先就是quick union，想法比较简单，首先就是初始化有N个元素的数组，初始化的时候对面的index里面存储的就是index本身，然后比如union 1 和 9 两个点就把他们对应的哪个component里面的所有元素的值都改为一样。优点：在看两个点是否是connect的时候 时间复杂度是1 缺点：union的时候N个元素的时间复杂度是 $O(N^2)$，代码实现如下

public class QuickFindUF{
     private int [] id;
    public QuickFindUF(int N){
        id = new int[N];
        for (int i =0;i<N;i++){
               id[i] = i;
}
 }
    public boolean connected(int p, int q){
        return id[p] == return id[q];
          
}
   public void union(int p, int q){

            int pid = id[p];
            int qid = id [q];
            for (int i = 0;i<N;i++){
                    if (id[i] == pid){   id[i] = qid;}
}
  }

}    

 

接下来是quickUnion，其基本思想就是做成树的结构，首先初始化N长度的数组，然后对应的数组里面存储的是父节点，union的时候我们只需要一直找下去找到根节点，再把根节点连到另外个点的根节点就行，find的 时候只需要看根节点是否一样就行。优点：union的时间复杂度取决于树的深度 缺点：find的时间复杂度变高了。  下面是java实现

public class QuickUnionUF{
     private int [] id;
   public QuickUnionUF(int N){

        id = new int [N];
        for(int i = 0;i < N;i++){
          id[i] = i;
     }

  }
     public int root(int i){

           while(id[i] != i){  i = id[i];}
           return i;
      }
   public boolean connected(int p , int q){
                 int  rootP = root(p);
                 int rootQ = root(q);
                return rootP == rootQ;
          }

   public void union(int p , int q){
         int i = root(p);
         int j = root(q);
         id[i] = j;

         }

 }    

 有两种改进QuickUnionUF的方法

第一种 将更小的树（节点少）连接 到更大的树上（节点多），如下图所示

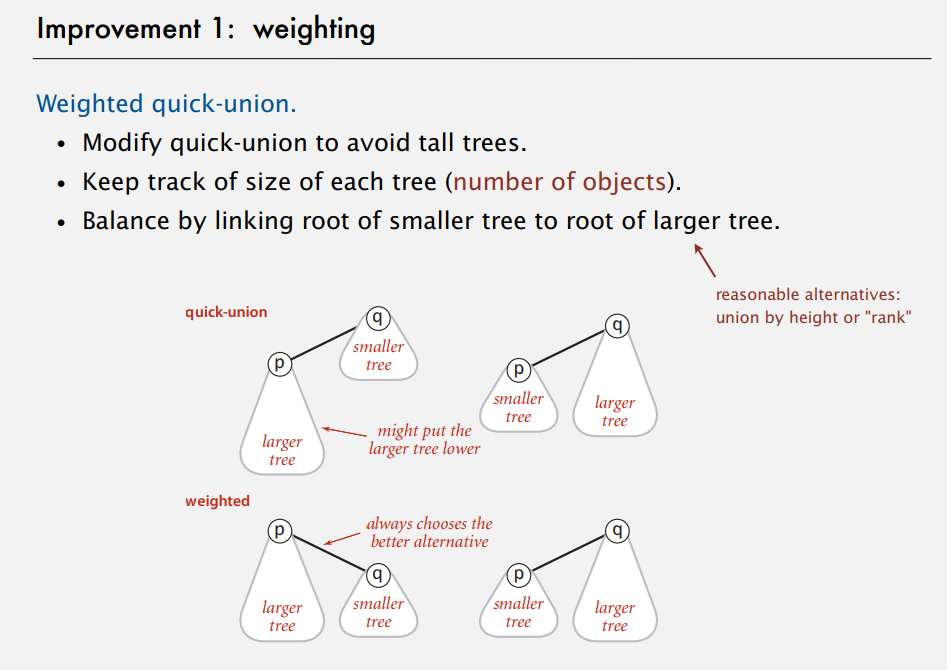
这种叫Weighted quick-union

下面是代码实现，find 和quick-union是一样的，union的代码需要一些修改，需要维护一个sz数组，用于存储树的大小。

 

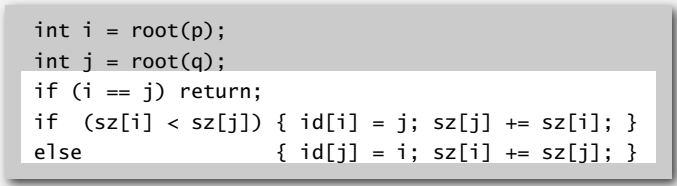
接下来是 Weighted quick-union 的性能分析

find和union操作是和p和q的深度成正比。但是这个算法任何节点x的深度不会超过lg N  这里lg指的是2为底。

proof：含有x节点的树什么时候深度会增加呢？只有当树T1 融合了 T2，而包含了x节点的树想要增加深度，至少整个树的节点就要翻倍因为$ \left| T_1 \right| \geqslant \left| T_2 \right|$, 这样一来含有x的树的节点数最多翻倍lg N次，深度最多就是lg N.

第二种 是通过路径压缩的方法

Quick union with path compression

这种方法就是在计算p节点的根节点的时候，把路径上的所有除根节点以外的节点，连接到根节点上，从而降低树的高度。实现方法有两种，一种是分两步Two-pass implementation，一种是一步直接达成Simpler one-pass variant。代码如下

Two-pass implementation  java implementation

public int root(int i ){
     int j = i;
     int root;
     while(i != id[i]){i = id[i];}
     root = i;
     while( j != id[j] ){ 
                int k = j;
                j = id [j]
                id[k] = root
}
   return root;

}

 Simp;er one-pass variant

public int root( int p){
      while(i != id[i]){

        id[i] = id[id[i]]
        i = id [i];
    }
     return i;
}

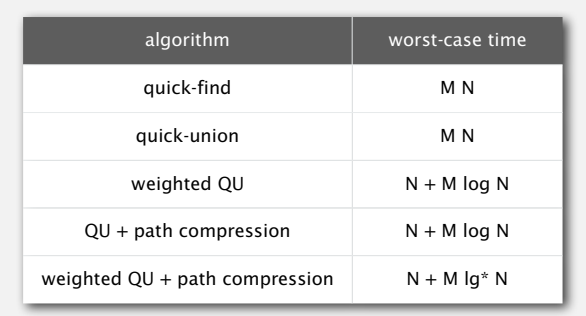
下面是一些性能分析的总结