洛谷题解：P12364 [蓝桥杯 2022 省 Python B] 寻找整数

注：可以在两分钟内跑出。

看到这题，暴力枚举跑不出来。如果你有没有充分的数学知识，那又怎么办呢？

减少枚举量

首先，注意到许多余数都是 \(11\)，有图为证：

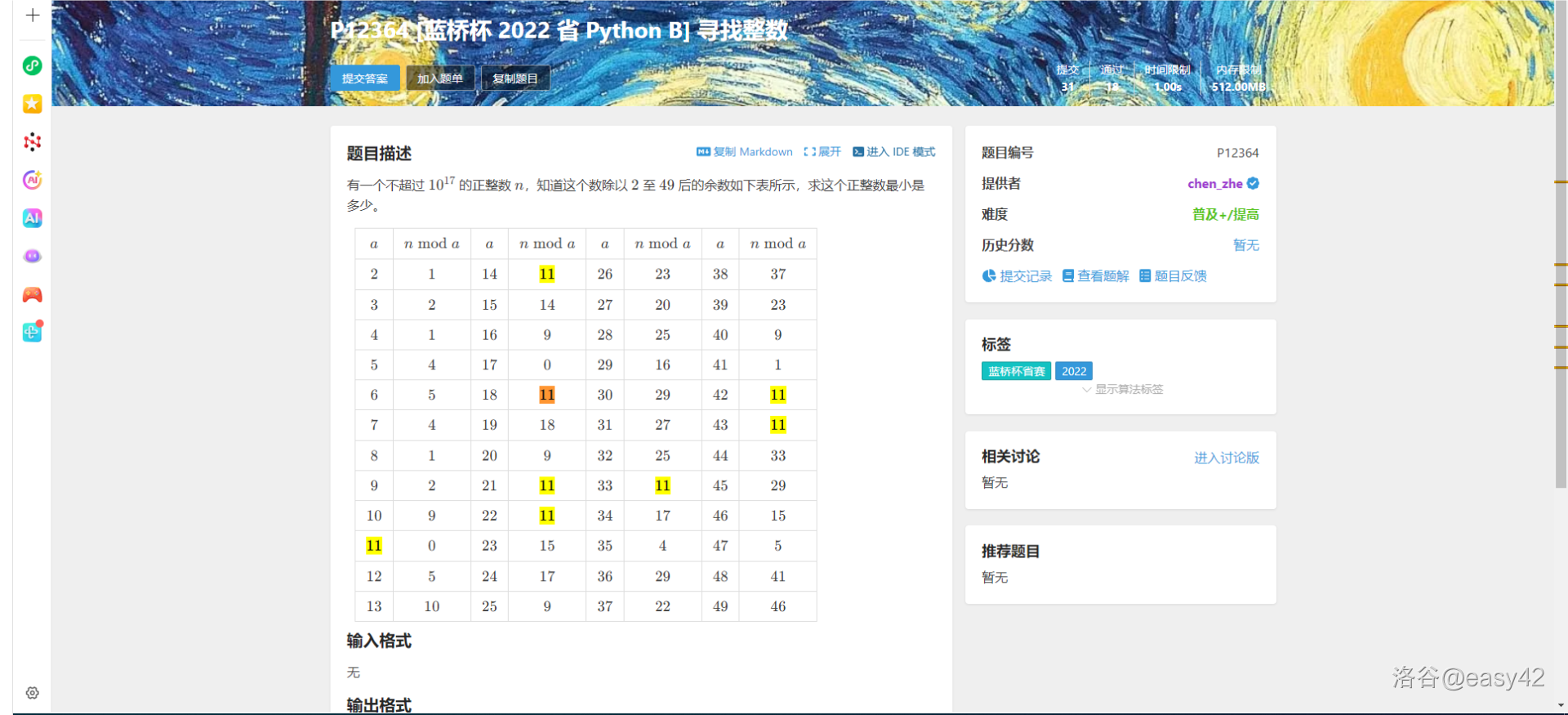
设这个数为 \(n\)，则有：

\[n \bmod 14 = n \bmod 18 =n \bmod 21 = n \bmod 22 = n \bmod 33 = n \bmod 42 = n \bmod 43 = 11 \]

直接把以上除数的最小公倍数求出，为 \(59598\)。

枚举时，我们设 \(n\) 为 \(i \times 59598+11\)，\(i\) 为循环变量。

它是满足所有以上 \( n \bmod 14 = n \bmod 18 =n \bmod 21 = n \bmod 22 = n \bmod 33 = n \bmod 42 = n \bmod 43 = 11 \) 的。

现在 \(i\) 只需枚举到 \(10^{13}\) 即可，因为 \(n\) 不超过 \(10^{17}\)。

暴力枚举

因为这个数肯定存在，所以只要使用一些（不一定要全部）条件，只搜出一个解即为答案。

需要注意的点：

1. 上界为 \(10^{13}\)。
2. 条件多加。
3. 耐心等待。

code

#include<bits/stdc++.h>
using namespace std;
long long n;
int main(){
	for(long long i=0;i<=10000000000000;i++){
		if((i*59598+11)%38==37&&(i*59598+11)%31==27&&(i*59598+11)%39==23&&(i*59598+11)%46==15&&(i*59598+11)%48==41&&(i*59598+11)%13==10&&(i*59598+11)%41==1&&(i*59598+11)%11==0&&(i*59598+11)%19==18&&(i*59598+11)%37==22&&(i*59598+11)%49==46&&(i*59598+11)%5==4&&(i*59598+11)%41==1&&(i*59598+11)%17==0){
			cout<<i<<" "<<i*59598+11<<endl;
            exit(0);
		}
	}
	return 0;
} 

最终代码：

print(2022040920220409)

求赞！