外卖配送时间优化系统课设报告
外卖配送时间优化系统
一、设计目的
本项目旨在利用数据结构组织配送网络信息,设计高效算法优化外卖配送路径,解决外卖配送过程中面临的路径规划问题。该系统通过合理规划骑手的取餐和送餐顺序,减少配送总距离和时间,提高配送效率,满足实际应用需求。在当前外卖行业高速发展的背景下,配送效率直接影响用户体验和平台运营成本,因此开发一套高效的配送路径优化系统具有重要的实用价值。
二、设计任务
本项目选择难度系数0.9的"外卖送餐最短路径设计"任务,具体要求如下:
- 外卖员取餐后可能会针对某一区域附近的客户同时取餐,再分别送餐,最后回到出发点
- 需要设计算法安排外卖员的送餐路线,使总行程最短
- 采用带权图来进行设计,权重表示路径长度
在此基础上,我们对任务进行了扩展,使系统具有更强的实用性:
- 支持用户设置骑手一次最多取1-5个餐
- 自动计算最优起始店面
- 规划完整的配送路径,包括取餐和送餐的顺序
- 可视化配送路径,直观展示配送过程
三、设计要求
1. 数据结构类型设计
1.1 逻辑结构设计
通过分析外卖配送网络的实际情况,我们将系统的逻辑结构设计为图结构,具体包括:
-
图结构:用于表示配送网络,包含店面节点和客户节点,边表示两点间的距离
- 节点类型:店面节点(1-10)和客户节点(101及以上)
- 边权重:表示两节点之间的距离
-
订单结构:记录客户订单信息
- 客户订单与店面的对应关系
- 待配送订单列表
-
配送状态结构:记录当前配送状态
- 已取未送的订单列表
- 节点访问状态
- 配送路径记录
-
最优路径结构:保存计算得到的最优配送路径
1.2 物理结构设计
考虑到系统需要频繁进行路径查询和距离计算,我们选择了以下物理结构来实现:
-
邻接矩阵:存储配送网络中各节点之间的距离
- 实现:二维数组
graph[MAX_NODES][MAX_NODES] - 理由:邻接矩阵适合稠密图,且可以快速查询任意两点间距离
- 实现:二维数组
-
数组:存储客户订单、配送状态等信息
- 客户订单对应店面:数组
customer_store[MAX_NODES] - 节点访问状态:数组
visited[MAX_NODES] - 最优路径:数组
optimal_path[MAX_NODES * 2] - 当前取餐状态:数组
curr_orders[MAX_PICKUPS] - 待配送订单:数组
pending_orders[MAX_CUSTOMERS]
- 客户订单对应店面:数组
2. 数据元素和数据项设计
根据系统需求,我们设计了以下数据元素和数据项:
2.1 数据元素
-
店面节点:表示餐厅
- 数据项:店面ID(1-10整数)
-
客户节点:表示下单客户
- 数据项:客户ID(101及以上整数)
-
路径:表示两个节点之间的连接
- 数据项:起点ID、终点ID、距离
-
订单:表示客户的订餐信息
- 数据项:客户ID、店面ID
2.2 数据项
-
配送网络图:存储所有节点间的距离关系
- 数据元素:店面节点、客户节点、路径
-
订单信息:存储所有客户的订单
- 数据元素:订单
-
配送状态:记录当前配送过程中的状态
- 数据元素:已取订单、已访问节点
-
配送路径:记录完整的配送路径
- 数据元素:路径节点序列
3. 输入文件分析
系统使用两个输入文件来构建配送网络和订单信息,下面对这两个文件进行详细分析:
3.1 配送网络数据文件(delivery_data.txt)
该文件存储了配送网络中各节点之间的距离信息,包括店面之间、店面到客户之间以及客户之间的距离。
文件格式:
[店面/客户ID] [店面/客户ID] [距离]
数据组织特点:
- 店面ID从1开始编号
- 客户ID从101开始编号
- 文件使用注释行(以#开头)组织不同类型的距离数据
- 距离数据表示为无向图,即A到B的距离与B到A的距离相同
数据内容分析:
-
店面之间的距离:
1 2 30 # 店面1到店面2距离为30 1 3 45 # 店面1到店面3距离为45 1 4 50 # 店面1到店面4距离为50 2 3 35 # 店面2到店面3距离为35 2 4 25 # 店面2到店面4距离为25 3 4 40 # 店面3到店面4距离为40共有4个店面,形成一个完全图,每两个店面之间都有直接连接。
-
店面到客户的距离:
# 店面1到客户的距离 1 101 15 # 店面1到客户101距离为15 1 102 22 # 店面1到客户102距离为22 ... # 店面2到客户的距离 2 101 25 # 店面2到客户101距离为25 ...每个店面到每个客户都有直接连接,表示骑手可以从任意店面直接前往任意客户位置。
-
客户之间的距离:
# 客户之间的距离(区域1: 101-103) 101 102 12 # 客户101到客户102距离为12 101 103 18 # 客户101到客户103距离为18 102 103 15 # 客户102到客户103距离为15 # 客户之间的距离(区域2: 104-106) 104 105 14 # 客户104到客户105距离为14 104 106 20 # 客户104到客户106距离为20 105 106 16 # 客户105到客户106距离为16客户被分为两个区域(区域1: 101-103,区域2: 104-106),同一区域内的客户订单可能来自不同店面,骑手需要在多个店面之间取餐,再在客户之间送餐。
通过分析可以看出,本配送网络具有以下特点:
- 总共有4个店面和6个客户
- 客户分布在两个不同区域
- 网络中共有(4+6)=10个节点,(6+24+6)=36条边
- 网络密度较高,适合使用邻接矩阵存储
3.2 客户点餐信息文件(客户拼好饭点餐店面信息.txt)
该文件存储了每个客户从哪个店面点餐的信息,用于构建订单关系。
文件格式:
[客户ID] [店面ID] # 注释
数据内容分析:
101 1 # 客户101从店面1点餐
102 2 # 客户102从店面2点餐
103 3 # 客户103从店面3点餐
104 4 # 客户104从店面4点餐
105 1 # 客户105从店面1点餐
106 2 # 客户106从店面2点餐
通过分析可以看出:
- 总共有6个客户订单
- 店面1有2个订单(客户101、105)
- 店面2有2个订单(客户102、106)
- 店面3有1个订单(客户103)
- 店面4有1个订单(客户104)
- 区域1(客户101-103)的订单分别来自店面1、2、3
- 区域2(客户104-106)的订单分别来自店面4、1、2
这种订单分布模式增加了配送路径规划的复杂性,因为同一区域的客户订单可能来自不同店面,骑手需要在多个店面之间取餐,再在客户之间送餐。
四、算法设计与分析
1. 算法设计思路
针对外卖配送路径优化问题,我们设计了以下算法思路:
-
最优起始点选择算法:通过枚举所有可能的起始店面,计算以每个店面为起点的总配送距离,选择总距离最短的店面作为最优起始点。
-
贪心配送路径算法:在配送过程中,采用贪心策略选择下一个访问节点:
- 优先送已取的餐(减少取餐后长时间配送导致的食品变质问题)
- 如果没有已取的餐,尝试去最近的店面取餐
- 取餐时,如果已达到最大取餐数量,则不再取更多的餐
-
最近邻节点选择算法:在每一步选择下一个访问节点时,寻找距离当前节点最近且满足条件的节点。
2. 核心算法分析
2.1 最近邻节点选择算法
int find_nearest(int current_node, int max_pickups) {
int nearest_node = -1;
int min_distance = INF;
// 首先检查是否需要送餐(已取的餐)
for (int i = 0; i < order_count; i++) {
int customer = curr_orders[i];
if (!visited[customer] && graph[current_node][customer] < min_distance) {
min_distance = graph[current_node][customer];
nearest_node = customer;
}
}
// 如果没有需要立即送的餐,且未达到最大取餐数量,考虑取餐
if (nearest_node == -1 && order_count < max_pickups) {
// 查找未访问的店面,且有客户等待该店面的餐
for (int i = 1; i <= MAX_STORES; i++) {
if (!visited[i]) {
// 检查是否有未配送的订单来自这个店面
int has_pending_orders = 0;
for (int j = 0; j < pending_count; j++) {
int customer = pending_orders[j];
if (!visited[customer] && !is_customer_order_picked(customer) && customer_store[customer] == i) {
has_pending_orders = 1;
break;
}
}
if (has_pending_orders && graph[current_node][i] < min_distance) {
min_distance = graph[current_node][i];
nearest_node = i;
}
}
}
}
return nearest_node;
}
算法选择分析:
在设计最近邻节点选择算法时,我们考虑了多种可能的实现方案:
-
纯最近邻算法(Pure Nearest Neighbor):最简单的贪心策略,每次仅选择距离当前节点最近的下一个节点。这种算法计算效率高(时间复杂度O(n)),但完全不考虑业务约束,可能导致取餐后长时间不送餐,造成食品变质。
-
禁忌搜索(Tabu Search):通过维护禁忌表避免重复访问近期访问过的节点,可以跳出局部最优。但这种方法需要额外的禁忌表维护,实现复杂,且不能直接应用于有业务约束(如先送已取餐)的场景。
-
基于规则的启发式算法(Rule-based Heuristic):根据业务规则设定优先级,如我们最终选择的分级优先级算法。这种方法能够在保持计算效率的同时,融入业务逻辑。
-
蚁群算法(Ant Colony Optimization):模拟蚂蚁寻找食物的路径优化过程,通过信息素更新迭代找到优质解。虽然能够得到较好的解,但算法复杂度高,需要多次迭代,不适合实时决策场景。
-
模拟退火算法(Simulated Annealing):通过概率接受劣解以跳出局部最优。该算法能够平衡全局探索和局部开发,但收敛慢,参数调优复杂。
最终,我们选择了基于业务规则的分级优先级算法,因为:
- 业务适应性:明确的优先级策略(先送餐,再取餐)直接符合外卖配送的实际业务需求
- 计算效率:时间复杂度O(MAX_STORES * pending_count),适合实时决策场景
- 实现简单:无需复杂参数调优,易于理解和维护
- 实用性:在同一优先级内仍采用贪心策略,保持了路径优化能力
- 食品质量保障:优先送已取的餐,减少食品变质风险
相比于其他复杂的元启发式算法(如蚁群算法、模拟退火算法),我们的算法在满足业务需求的前提下,具有更高的实用性和效率。
2.2 配送路径优化算法
void optimize_delivery(int start_node, int max_pickups) {
// 重置状态
path_length = 0;
order_count = 0;
for (int i = 0; i < MAX_NODES; i++) {
visited[i] = 0;
}
int current_node = start_node;
optimal_path[path_length++] = current_node;
while (!all_completed()) {
// 查找最近的下一个节点
int next_node = find_nearest(current_node, max_pickups);
// 处理特殊情况...
// 更新路径和当前节点
optimal_path[path_length++] = next_node;
current_node = next_node;
// 更新取餐和送餐状态...
}
}
算法选择分析:
在设计配送路径优化算法时,我们比较了多种可能的实现方案:
-
穷举法(Brute Force):遍历所有可能的配送路径,选择总距离最短的路径。这种方法会得到全局最优解,但时间复杂度为O(n!),随着节点数量增加,计算量呈指数级增长,完全不适合实际应用。
-
分支定界法(Branch and Bound):通过设定上下界剪枝,减少搜索空间。虽然在最坏情况下时间复杂度仍为O(n!),但实际运行时间通常比穷举法好。然而,对于中等规模以上的问题,计算量仍然过大。
-
遗传算法(Genetic Algorithm):通过模拟自然进化过程(选择、交叉、变异)来优化路径。这种方法可以处理大规模问题,但收敛速度慢,且调参复杂,结果质量受初始种群影响大。
-
蚁群算法(Ant Colony Optimization):通过模拟蚂蚁觅食行为优化路径。能够处理大规模问题,但同样面临参数调优困难、迭代次数多的问题。
-
贪心算法(Greedy Algorithm):每一步都选择当前最优的选择,如我们实现的多级优先级贪心算法。时间复杂度低,适合实时决策,但不保证全局最优解。
-
动态规划(Dynamic Programming):对于经典的TSP问题,可以使用DP求解,但由于我们的问题增加了取餐数量限制、业务逻辑约束等,传统DP方法需要大量修改才能适用。
最终,我们选择了基于多级优先级的贪心算法,主要基于以下考虑:
- 计算效率:时间复杂度为O(pending_count² * MAX_STORES),在实际应用规模下可以快速得到解
- 业务约束集成:能够自然地融入业务逻辑(如最大取餐数量限制、先送已取餐等)
- 增量式决策:适合实时决策场景,可以根据新订单动态调整路径
- 实现简单:无需复杂的数学模型和参数调优,容易理解和维护
- 解的质量:虽不保证全局最优,但通过多级优先级策略,在满足业务约束的前提下,能够得到实用的近似解
相比之下,动态规划、遗传算法等方法虽然在解的质量上可能有优势,但在计算效率、业务约束集成和实现复杂度上存在明显劣势,不适合我们的应用场景。
2.3 最优起始店面算法
int find_optimal_start_store(int max_pickups) {
int best_start = 1;
int min_total_distance = INF;
// 尝试每个店面作为起始点
for (int start = 1; start <= MAX_STORES; start++) {
// 检查该店面是否有订单
int has_orders = 0;
for (int i = 0; i < pending_count; i++) {
if (customer_store[pending_orders[i]] == start) {
has_orders = 1;
break;
}
}
if (!has_orders) {
continue; // 跳过没有订单的店面
}
// 计算以该店面为起点的路径
optimize_delivery(start, max_pickups);
// 计算总距离
int total_distance = calculate_total_distance(optimal_path, path_length);
// 更新最优起点
if (total_distance < min_total_distance) {
min_total_distance = total_distance;
best_start = start;
}
}
return best_start;
}
算法选择分析:
在设计最优起始店面算法时,我们考虑了多种可能的方法:
-
随机选择(Random Selection):随机选择一个店面作为起点。这是最简单的方法,但完全不考虑优化目标,解的质量无法保证。
-
启发式方法(Heuristic Methods):
- 最大订单数量:选择订单数量最多的店面作为起点。实现简单,但忽略了空间分布因素。
- 地理中心性:选择到所有节点距离和最小的店面。考虑了空间分布,但未考虑实际配送过程。
- 最近邻聚类中心:计算所有配送节点的聚类中心,选择最接近中心的店面。考虑到了节点分布,但聚类中心计算复杂且可能不在网络上。
-
机器学习方法(Machine Learning):通过历史数据训练模型,预测最优起始店面。这种方法需要大量历史数据,且模型训练和维护成本高。
-
模拟法(Simulation):
- 蒙特卡洛模拟:随机采样多个起始点,对每个点模拟配送过程,选择平均表现最好的。
- 对比试验:我们选择的枚举法,即对每个可能的起始店面都完整规划一次配送路径,选择总距离最短的方案。
-
数学规划(Mathematical Programming):建立起始点选择的数学模型,使用线性规划或整数规划求解。这种方法需要专业的优化求解器,实现复杂。
最终,我们选择了枚举法(对比试验),主要基于以下考虑:
- 确定性:通过实际计算每个起始点的完整配送路径,得到的结果最为可靠
- 全局视角:考虑了完整的配送过程,而不仅仅是起始点的局部特性
- 适用性:不依赖历史数据或复杂模型,适用于各种场景
- 计算可行性:虽然需要为每个起始店面计算一次完整路径,但由于店面数量通常有限(本系统中为4个),总体计算量可接受
- 解的质量:在给定的配送路径优化算法下,能够找到真正的最优起始店面
相比之下,其他方法或者计算效率更高但解的质量无法保证(如启发式方法),或者实现复杂度高且依赖外部资源(如机器学习方法、数学规划方法)。综合考虑实用性和解的质量,枚举法是最适合我们应用场景的选择。
2.4 算法复杂度汇总分析
| 算法 | 时间复杂度 | 空间复杂度 | 详细分析 |
|---|---|---|---|
| 最近邻节点选择算法 | O(n) | O(1) | 检查已取餐:O(max_pickups) 查找店面:O(MAX_STORES * pending_count) 总体时间复杂度:O(MAX_STORES * pending_count) 只使用了常数级的额外空间 |
| 配送路径优化算法 | O(n²) | O(n) | 外层循环执行次数:O(pending_count),即客户订单数量 每次循环内部查找最近节点:O(MAX_STORES * pending_count) 总体时间复杂度:O(pending_count² * MAX_STORES) 存储路径和访问状态:O(MAX_NODES) |
| 最优起始店面算法 | O(m·n²) | O(n) | 外层循环执行次数:O(MAX_STORES) 每次循环调用optimize_delivery:O(pending_count² * MAX_STORES) 总体时间复杂度:O(MAX_STORES² * pending_count²) 调用optimize_delivery使用的空间:O(MAX_NODES) |
| 数据读取算法 | O(e) | O(n²) | e表示边的数量,n表示节点数量 使用邻接矩阵存储图结构,空间复杂度为O(n²) |
| 初始化图结构 | O(n²) | O(n²) | 需要初始化n×n的邻接矩阵和n个节点的状态数组 |
| 总体系统 | O(m·n²) | O(n²) | 受限于最优起始店面算法的时间复杂度O(MAX_STORES² * pending_count²) 和邻接矩阵的空间复杂度O(MAX_NODES²) |
3. 算法优化
我们针对上述算法进行了以下优化:
- 贪心策略优化:采用多层次的贪心策略,优先考虑已取餐的配送,减少食品变质风险。
- 最大取餐数量限制:引入最大取餐数量参数,避免骑手一次取太多餐导致的配送延迟。
- 最优起始点选择:通过枚举所有可能的起始店面,找到全局最优的起始点。
- 路径可视化:实现了配送路径的可视化,便于直观理解和评估配送方案。
五、代码实现
1. 数据结构定义
// 存储店面和客户之间的距离
int graph[MAX_NODES][MAX_NODES];
// 存储客户订单对应的店面
int customer_store[MAX_NODES];
// 所有节点的访问状态
int visited[MAX_NODES];
// 最优路径
int optimal_path[MAX_NODES * 2];
int path_length = 0;
// 配送员当前取餐状态
int curr_orders[MAX_PICKUPS];
int order_count = 0;
// 待配送的订单
int pending_orders[MAX_CUSTOMERS];
int pending_count = 0;
2. 主要函数实现
2.1 初始化图结构
void init_graph() {
for (int i = 0; i < MAX_NODES; i++) {
for (int j = 0; j < MAX_NODES; j++) {
if (i == j) {
graph[i][j] = 0;
} else {
graph[i][j] = INF;
}
}
visited[i] = 0;
customer_store[i] = -1;
}
}
2.2 数据读取
void read_delivery_data(const char* filename) {
FILE* file = fopen(filename, "r");
if (file == NULL) {
printf("无法打开文件: %s\n", filename);
exit(1);
}
char line[100];
int node1, node2, distance;
while (fgets(line, sizeof(line), file)) {
// 跳过注释行
if (line[0] == '#' || line[0] == '\n') {
continue;
}
// 解析行数据
if (sscanf(line, "%d %d %d", &node1, &node2, &distance) == 3) {
graph[node1][node2] = distance;
graph[node2][node1] = distance; // 无向图
}
}
fclose(file);
}
2.3 主程序流程
int main() {
int max_pickups = 3; // 默认骑手一次最多取3个餐
int store_customer_count[MAX_STORES+1] = {0}; // 每个店面的客户数量
// 初始化系统
init_graph();
// 读取数据
read_delivery_data("delivery_data.txt");
read_customer_store_data("客户拼好饭点餐店面信息.txt");
// 按店面分组客户订单信息
group_orders_by_store(store_customer_count);
// 自动寻找最优起始店面
int optimal_start = find_optimal_start_store(max_pickups);
// 使用最优起始店面进行配送路径规划,并打印详细过程
print_delivery_process(optimal_start, max_pickups);
// 显示结果
print_optimal_path();
// 保存到CSV
save_to_csv("optimal_routes.csv");
return 0;
}
3. 运行结果
系统运行结果如下:
(base) User@MacBookAir 外卖配送时间优化 % cd "/Users/User/Desktop/外卖配送时间优化/"
&& gcc main.c -o main && "/Users/User/Desktop/外卖配送时间优化/"main
外卖配送时间优化系统
========================
请输入骑手一次最多能取的餐数量 (1-5,默认为3): 3
------------------------
初始化系统...
读取配送网络数据...
读取客户点餐信息...
读取到客户 101 从店面 1 点餐
读取到客户 102 从店面 2 点餐
读取到客户 103 从店面 3 点餐
读取到客户 104 从店面 4 点餐
读取到客户 105 从店面 1 点餐
读取到客户 106 从店面 2 点餐
------------------------
共有 6 个客户订单
各店面订单分布:
店面 1: 2 个订单
店面 2: 2 个订单
店面 3: 1 个订单
店面 4: 1 个订单
------------------------
配送参数设置:
骑手一次最多取 3 个餐
正在计算最优起始店面...
从店面 1 开始:总距离 = 188
从店面 2 开始:总距离 = 175
从店面 3 开始:总距离 = 191
从店面 4 开始:总距离 = 197
最优起始店面是:店面 2 (总距离: 175)
开始配送过程...
------------------------
取餐:从店面 2 取餐,送往客户 102
取餐:从店面 2 取餐,送往客户 106
送餐:将店面 2 的餐送到客户 102
取餐:从店面 1 取餐,送往客户 101
取餐:从店面 1 取餐,送往客户 105
送餐:将店面 1 的餐送到客户 101
取餐:从店面 4 取餐,送往客户 104
送餐:将店面 2 的餐送到客户 106
送餐:将店面 1 的餐送到客户 105
送餐:将店面 4 的餐送到客户 104
取餐:从店面 3 取餐,送往客户 103
送餐:将店面 3 的餐送到客户 103
------------------------
最优配送路径: 2 -> 2 -> 102 -> 1 -> 101 -> 4 -> 106 -> 105 -> 104 -> 3 -> 103
总配送距离: 175
已保存最优路径到 optimal_routes.csv
配送任务完成!

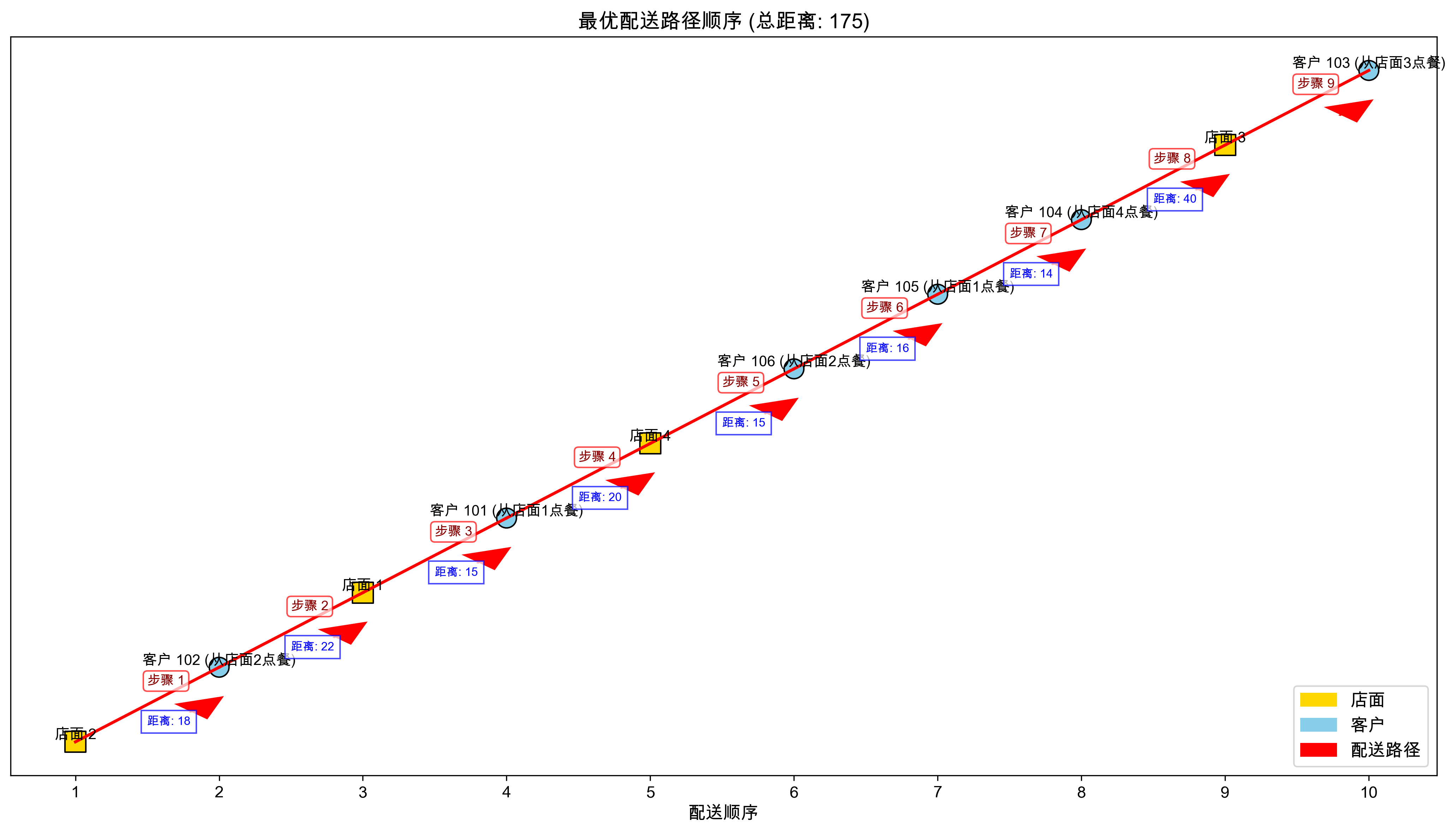
配送路径可视化展示了店面节点(黄色方块)、客户节点(蓝色圆形)以及最优配送路径(红色箭头线)。通过可视化结果可以直观地看到骑手的取餐、送餐路线。
算法找到的最优配送路径总距离为:175,涉及的配送节点数量为10个,包括4个店面和6个客户。
六、总结与反思
1. 系统特点
本系统具有以下特点:
- 支持用户自定义骑手最大取餐数量
- 自动计算最优起始店面
- 使用贪心算法规划最短配送路径
- 提供详细的配送过程描述
- 生成直观的配送路径可视化
2. 算法优势
- 效率高:贪心算法在每一步都选择局部最优解,计算效率高
- 灵活性:可以根据实际需求调整取餐数量限制
- 实用性:考虑了实际配送中的多种约束条件
3. 局限性
- 局部最优:贪心算法可能无法找到全局最优解
- 规模限制:当节点数量过大时,算法效率会降低
- 约束简化:实际配送中还存在时间窗口、交通状况等复杂因素,本系统做了简化处理
4. 未来改进方向
- 引入更复杂的启发式算法或元启发式算法,如模拟退火、遗传算法等
- 考虑时间窗口约束,更符合实际配送场景
- 加入实时交通数据,动态调整配送路径
- 支持多骑手协同配送优化
七、参考文献
- Toth, P., & Vigo, D. (2014). Vehicle routing: problems, methods, and applications. Society for Industrial and Applied Mathematics.
- Laporte, G. (1992). The vehicle routing problem: An overview of exact and approximate algorithms. European Journal of Operational Research, 59(3), 345-358.
- 孙康, 李斌, 王媛. (2018). 基于改进蚁群算法的外卖配送路径优化. 计算机应用, 38(10), 2923-2927.
- Cormen, T. H., Leiserson, C. E., Rivest, R. L., & Stein, C. (2009). Introduction to algorithms. MIT press.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号