数据结构考试用👹
数据元素、数据项、数据结构
数据元素是数据的基本单位,
数据项是数据的最小单位,
数据结构是带有结构的各数据元素的集合。
通常要求同一逻辑结构中的所有数据元素具有相同的特性,这意味着
数据元素所包含的数据项的个数相同,且对应数据项的类型要一致
2.线性表

算法设计:
(1)将两个递增的有序链表合并为一个递增的有序链表。要求结果链表仍使用原来两个链表的存储空间, 不另外占用其它的存储空间。表中不允许有重复的数据。
[题目分析]
合并后的新表使用头指针 Lc 指向,pa 和 pb 分别是链表 La 和 Lb 的工作指针,初始化为相
应链表的第一个结点,从第一个结点开始进行比较,当两个链表 La 和 Lb 均为到达表尾结点
时,依次摘取其中较小者重新链接在 Lc 表的最后。如果两个表中的元素相等,只摘取 La 表
中的元素,删除 Lb 表中的元素,这样确保合并后表中无重复的元素。当一个表到达表尾结
点,为空时,将非空表的剩余元素直接链接在 Lc 表的最后。
[算法描述]
void MergeList(LinkList &La, LinkList &Lb, LinkList &Lc)
{ // 合并链表 La 和 Lb,合并后的新表使用头指针 Lc 指向
pa = La->next;
pb = Lb->next;
// pa 和 pb 分别是链表 La 和 Lb 的工作指针,初始化为相应链表的第一个结点
Lc = pc = La; // 用 La 的头结点作为 Lc 的头结点
while (pa && pb)
{
if (pa->data`< pb->`data)
{
pc->next = pa;
pc = pa;
pa = pa->next;
}
// 取较小者 La 中的元素,将 pa 链接在 pc 的后面,pa 指针后移
else if (pa->data > pb->data)
{
pc->next = pb;
pc = pb;
pb = pb->next;
}
// 取较小者 Lb 中的元素,将 pb 链接在 pc 的后面,pb 指针后移8
else // 相等时取 La 中的元素,删除 Lb 中的元素
{
pc->next = pa;
pc = pa;
pa = pa->next;
q = pb->next;
delete pb;
pb = q;
}
}
pc->next = pa ? pa : pb;
// 插入剩余段
delete Lb;
// 释放 Lb 的头结点
}
(2)将两个非递减的有序链表合并为一个非递增的有序链表。要求结果链表仍使用原来
两个链表的存储空间, 不另外占用其它的存储空间。表中允许有重复的数据。
[题目分析]
合并后的新表使用头指针 Lc 指向,pa 和 pb 分别是链表 La 和 Lb 的工作指针,初始化为相
应链表的第一个结点,从第一个结点开始进行比较,当两个链表 La 和 Lb 均为到达表尾结点
时,依次摘取其中较小者重新链接在 Lc 表的表头结点之后,如果两个表中的元素相等,只摘
取 La 表中的元素,保留 Lb 表中的元素。当一个表到达表尾结点,为空时,将非空表的剩余
元素依次摘取,链接在 Lc 表的表头结点之后。
[算法描述]
void MergeList(LinkList &La, LinkList &Lb, LinkList &Lc, )
{ // 合并链表 La 和 Lb,合并后的新表使用头指针 Lc 指向
pa = La->next;
pb = Lb->next;
// pa 和 pb 分别是链表 La 和 Lb 的工作指针,初始化为相应链表的第一个结点
Lc = pc = La; // 用 La 的头结点作为 Lc 的头结点
Lc->next = NULL;
while (pa || pb)
{ // 只要存在一个非空表,用 q 指向待摘取的元素
if (!pa)
{
q = pb;
pb = pb->next;
}
// La 表为空,用 q 指向 pb,pb 指针后移
else if (!pb)
{
q = pa;
pa = pa->next;
}
// Lb 表为空,用 q 指向 pa,pa 指针后移
else if (pa->data <= pb->data)
{
q = pa;
pa = pa->next;
}
// 取较小者(包括相等)La 中的元素,用 q 指向 pa,pa 指针后移
else
{
q = pb;
pb = pb->next;
}
// 取较小者 Lb 中的元素,用 q 指向 pb,pb 指针后移
q->next = Lc->next;
Lc->next = q;
// 将 q 指向的结点插在 Lc 表的表头结点之后
}
delete Lb;
// 释放 Lb 的头结点
}
(3)设计一个算法,通过遍历一趟,将链表中所有结点的链接方向逆转,仍利用原表的存储空间。
[题目分析]
从首元结点开始,逐个地把链表 L 的当前结点 p 插入新的链表头部。
[算法描述]
void inverse(LinkList &L)
{ // 逆置带头结点的单链表 L
p = L->next;
L->next = NULL;
while (p)
{
q = p->next;
// q 指向*p 的后继
p->next = L->next;
L->next = p;
// *p 插入在头结点之后
p = q;
}
}
3.栈和队列

特殊值法。设 n=0,易知仅调用一次 fact(n)函数
循环队列
队空:rear == front
队满:(rear+1)%MAXSIZE==front,
入队:rear=(rear+1)%(m+1)
出队:front=(front + 1) % MAXSIZE;
4.树和二叉树
树的公式
n = 所有结点的度数之和 + 1
n = n0 + n1 + n2 + ...
第i层最多结点数 = m^(i-1)
i层最多结点数 = ( m^i ) / ( m-1 )
二叉树:n0 = n2 + 1
完全二叉树:
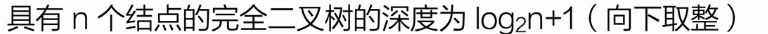
log向下取整:
最小树高 = [ log2(n) ] + 1
如果总结点数-1是奇数,说明有一个度为1的结点
哈夫曼树:
哈夫曼树没有n1的结点
二叉链表:
二叉链表的左指针 -> 子节点,右指针 -> 兄弟结点
线索化

- 先写出什么序遍历的结果
- 画出每个结点的左线索和右线索,左->前驱,右->后继
- 左线索和右线索会占用lchild和rchild
树与二叉树的转换
树-->二叉树
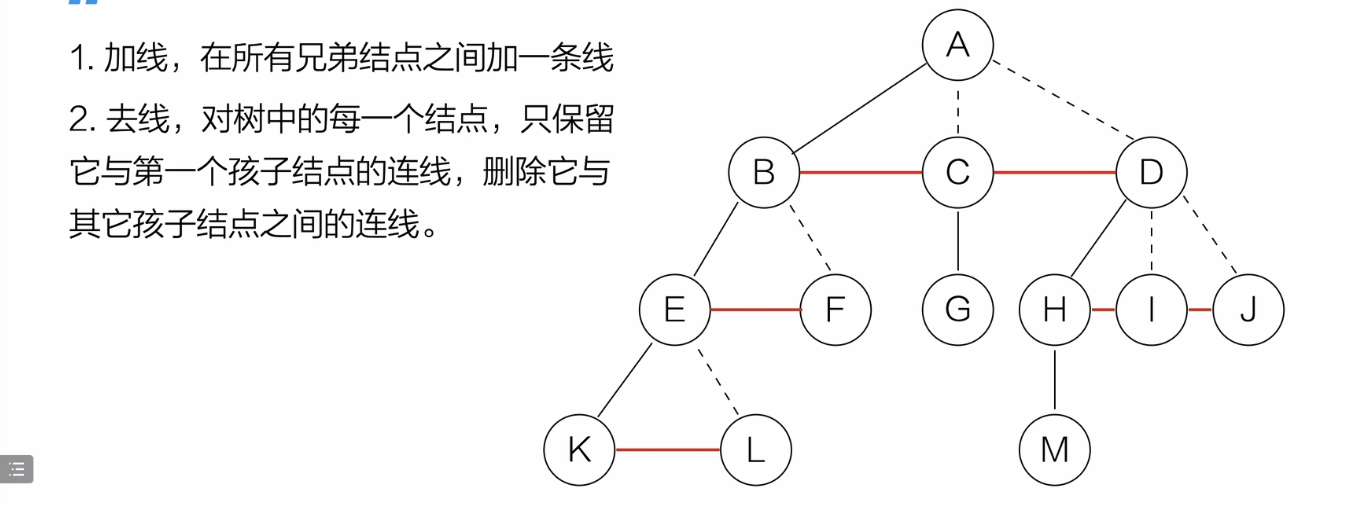
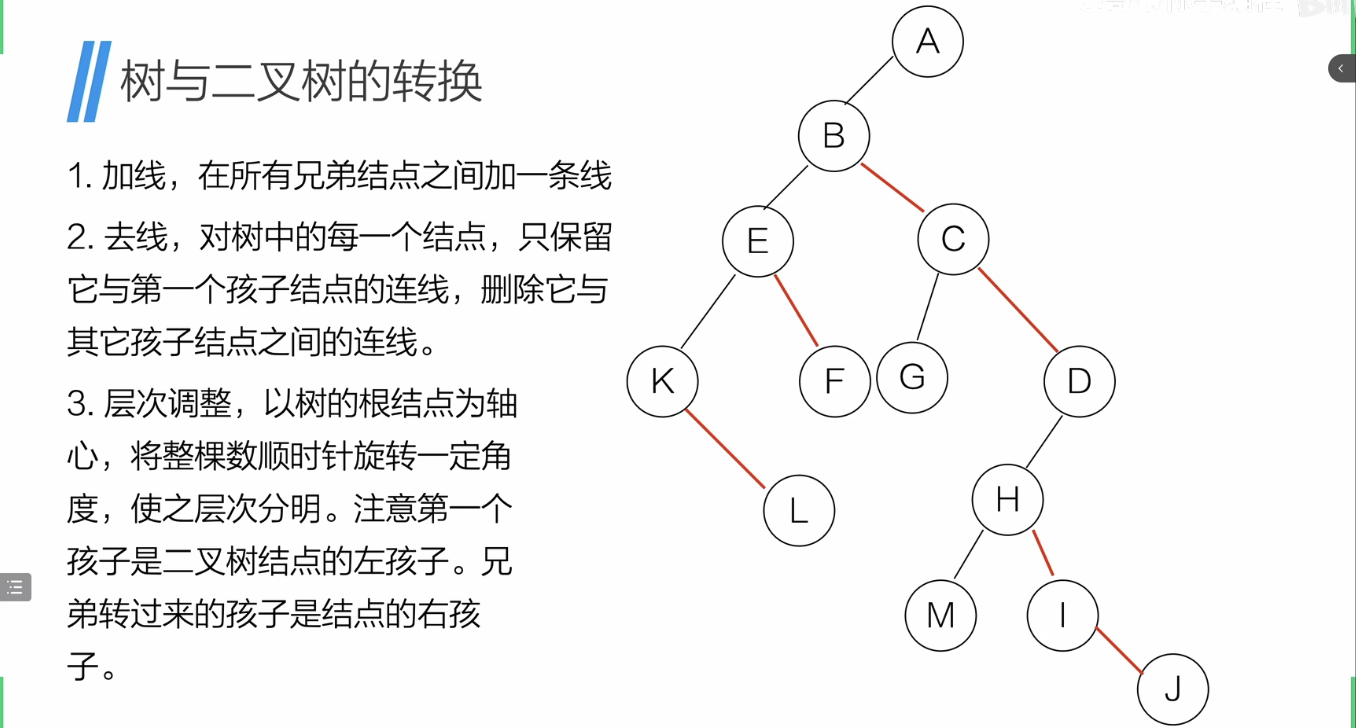
二叉树-->树
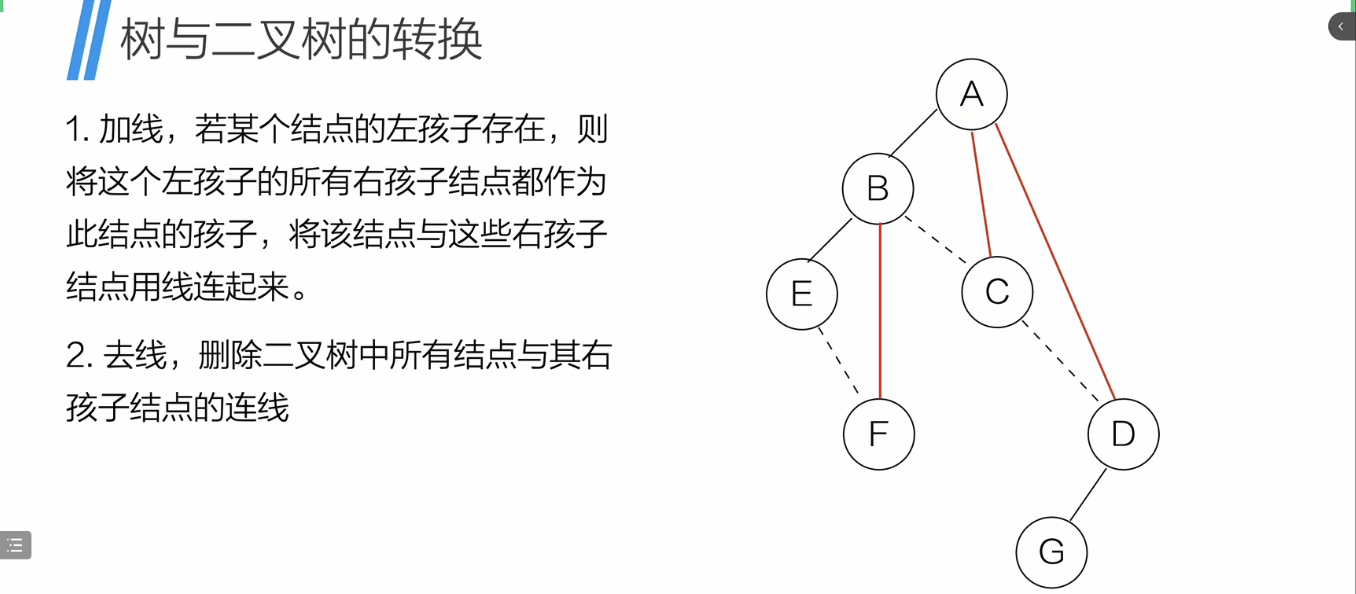
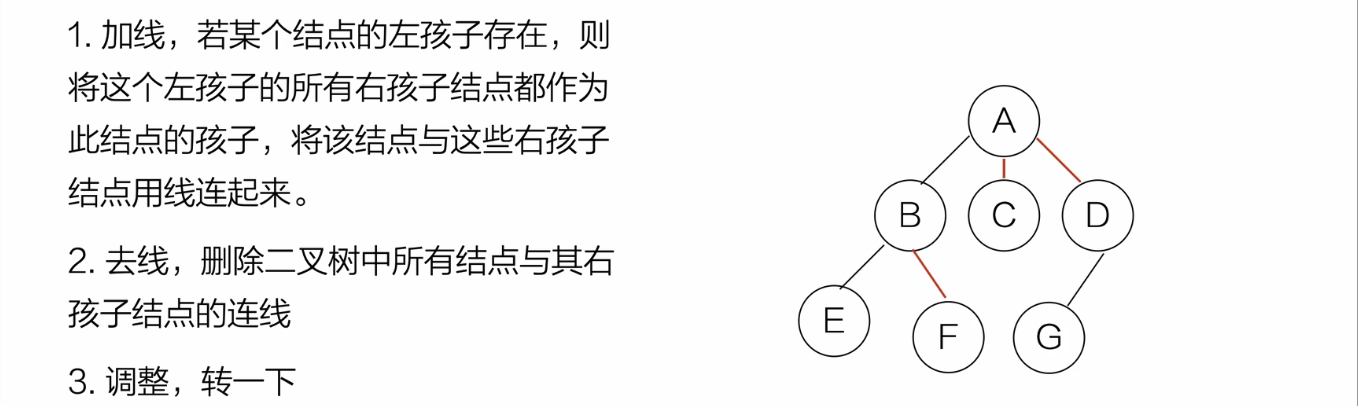
森林转二叉树
森林-->二叉树
-
把每个树各自转成二叉树

-
所有兄弟结点连线
-
只保留每个结点与第一个孩子的连线

-
旋转
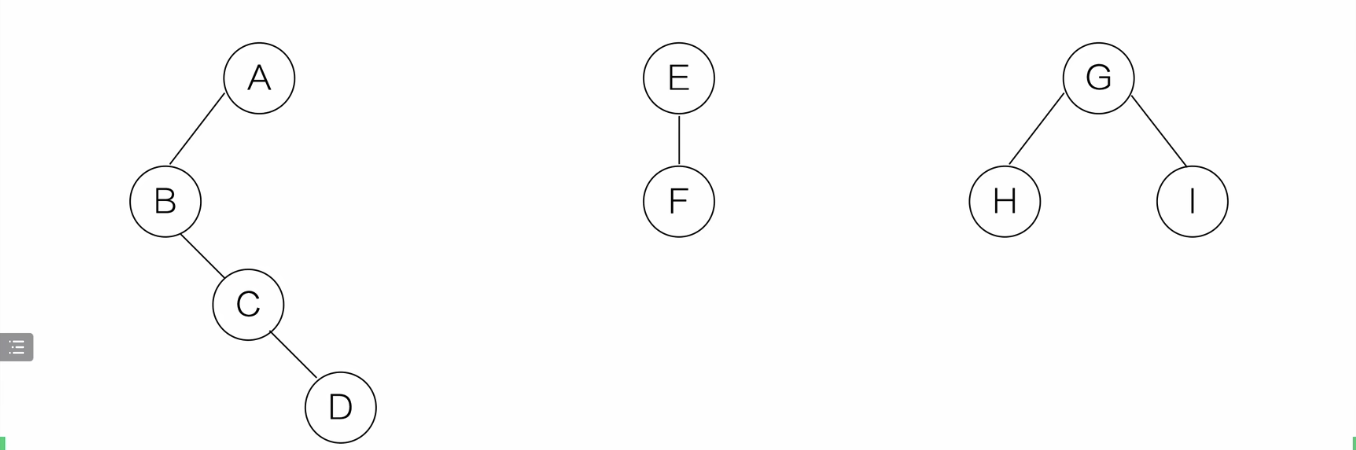
-
后面的树也这样操作
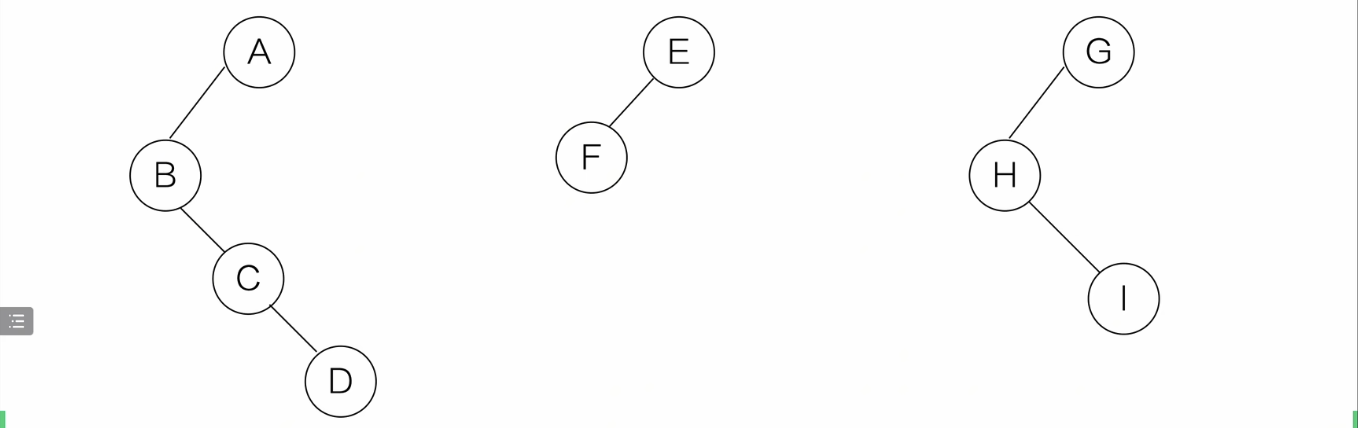
-
-
整合成一个二叉树


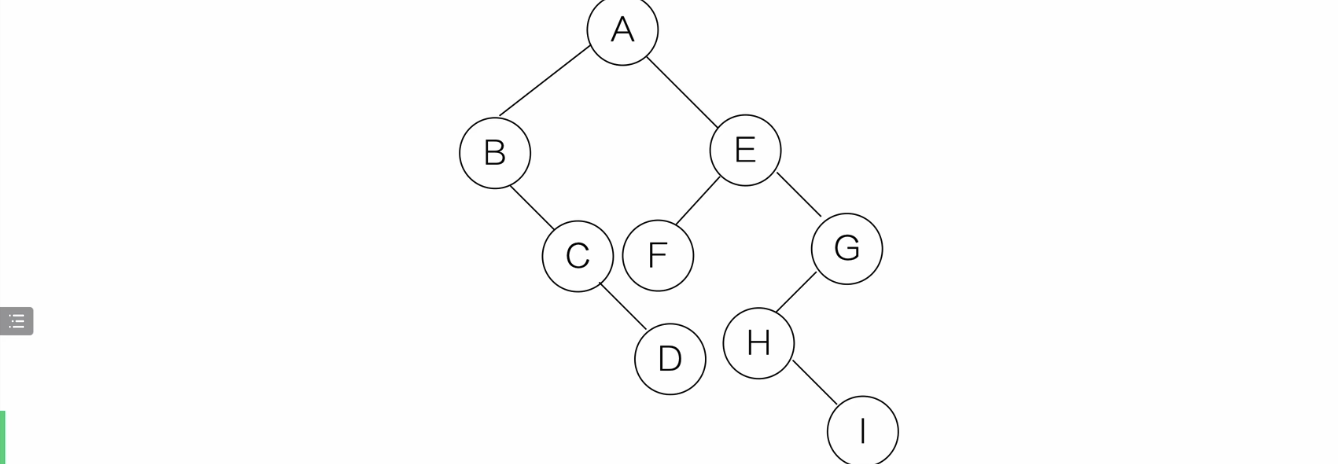
详细操作看《数据结构(C 语言描述)》的53:40左右进度条
二叉树-->森林
- 拆成多个二叉树
-
从根结点开始,右结点存在就删去与右孩子的连线
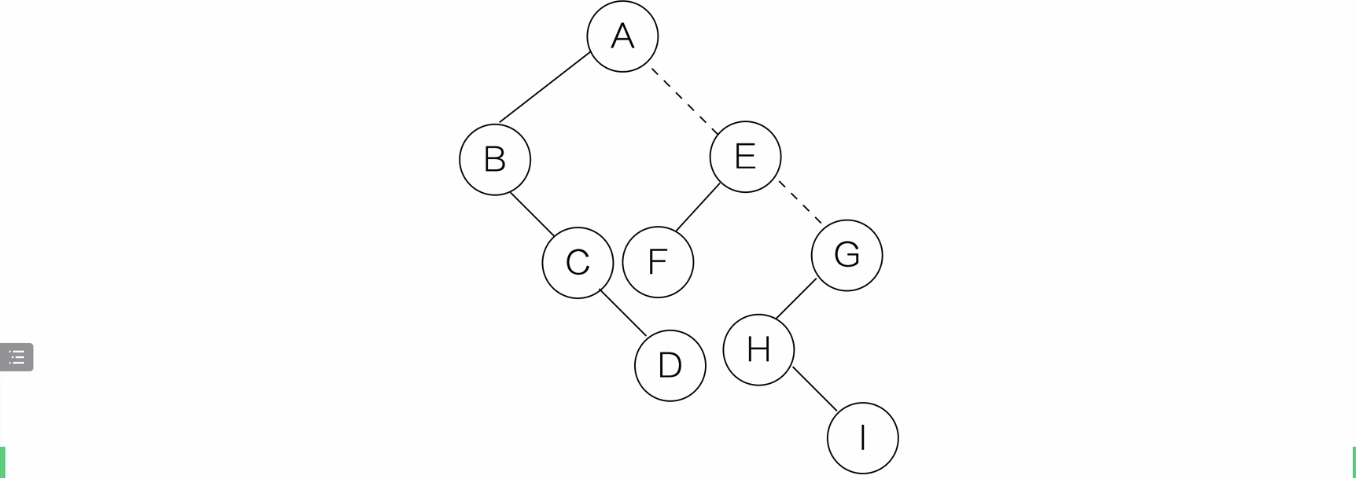
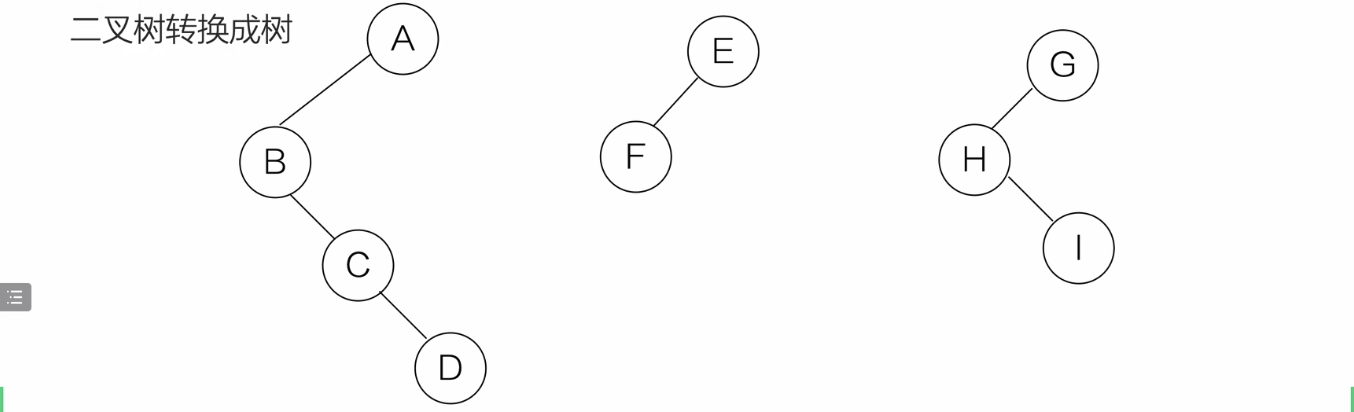
-
- 每个 二叉树->树
-
从根结点开始,若结点的左孩存在,就把该结点与左孩的所有右孩相连
-
删去兄弟结点的连线
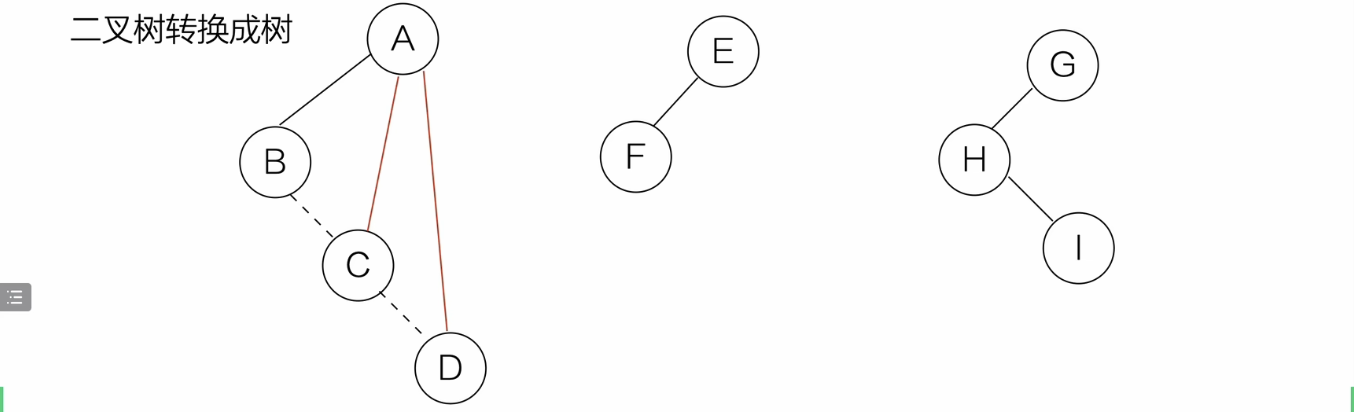
-
对每个二叉树做同样操作
-
旋转

-
5.图
所有顶点的度数和 = 边数 * 2
有向图:入度和 = 出度和
无向图的最大边数 = C(n,2) = n(n-1)/2
有向图的最大边数 = n(n-1)

DFS <=> 先序遍历
BFS <=> 层次遍历
画邻接矩阵:
带权值的写∞
不带权值的写0
7.查找
顺序查找:
ASL =( n(n+1) / 2 ) / n = (n+1) / 2
O(n)
折半查找(二分查找):
必须是已经排好序的有序数组,每次和中间的元素比较,如果比中间元素小,就在前半部分查找;否则在后半部分查找。
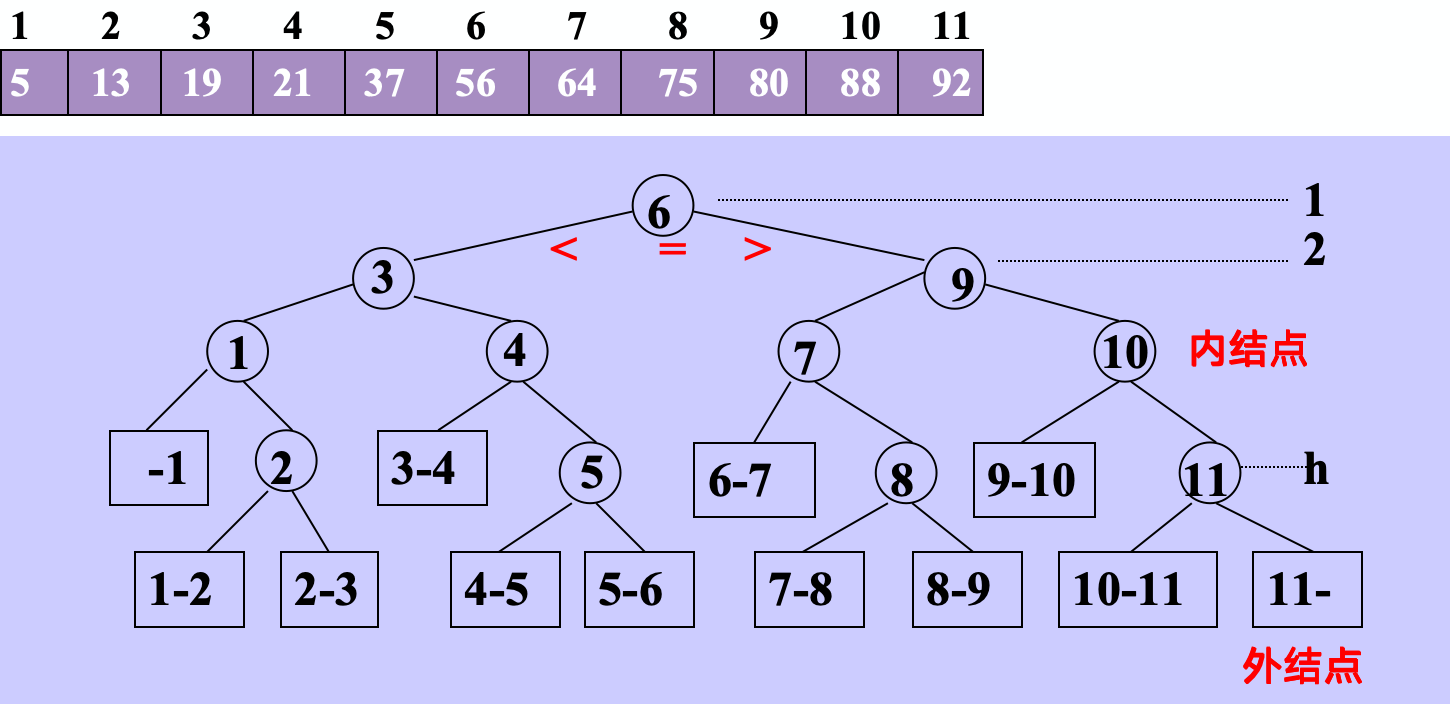
上图可以计算, ASL=1/11(11+2×2+4×3+4*4 )=33/11=3
ASL = log2(n)
O( log2 (n) )
分块查找:
线性表既能较快的查找,又能适应动态变化
对输入序列的要求分块有序,要求每个子表中的数值都比后一块中数值小(但子表内部未必有序)。
将各子表中的最大关键字构成一个索引表,表中还要包含每个子表的起始地址(即头指针):
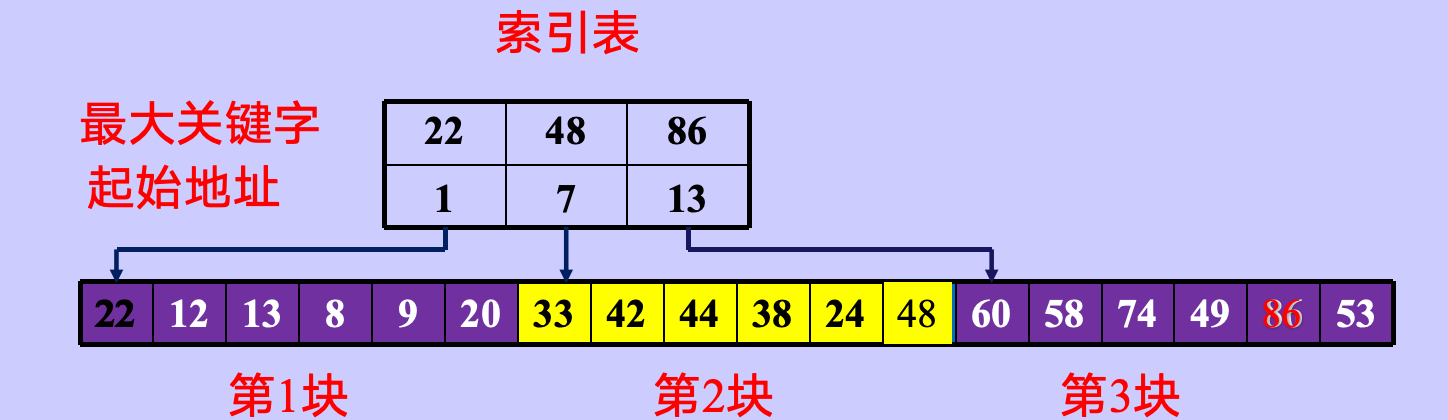
查找过程:
① 对索引表使用折半查找法,确定待查关键字所在的子表
② 在子表内采用顺序查找法(因为子表无序,只能挨个比对)。
O( log2 (n/s) + s )
s是子块的长度
二叉树查找:
左 < 根 < 右
查找过程:
- key == 根结点 ,返回
- 否则:
- key < 根结点,去这个结点的左子树找
- key > 根结点,去这个结点的右子树找
时间复杂度
最好:log2(n)
最坏:(n+1)/2
适合需要经常进行插入、删除和查找运算的表
哈希查找:
链地址法:把哈希地址一样的放在一条链上
ASL按链表的查找计算:第 i 个结点乘 i
8.排序
插入排序
直接插入排序(基于顺序查找):
工作原理类似理牌,在已排序列里面找到正确位置插入
- 时间复杂度为 O(n^2)
- 空间复杂度为 O(1)
- 是一种稳定的排序方法
- 平均情况比较次数和移动次数为(n^2) / 4
希尔排序(基于逐趟缩小增量dk):
- dk不为 1 的时候,把隔dk的两个值是否交换位置
- dk = 1 的时候,把隔dk的值作为基准与前面已排序列一一比较,找到正确位置插入。
时间复杂度是n和d的函数:
空间复杂度为 O(1)
是一种不稳定的排序方法
最后一个增量值必须为1
不宜在链式存储结构上实现
适合初始记录无序,n较大
交换排序
冒泡排序:
最好情况:输入序列是顺序,只需 1趟排序,比较 n-1 次,不移动
最坏情况:输入序列是逆序,需 n 趟排序,第i趟 比较 n -1 -i 次,移动3(n -1 -i)次
总比较次数:
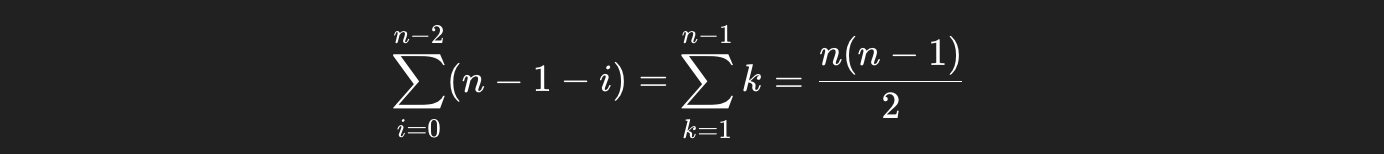
总移动次数:
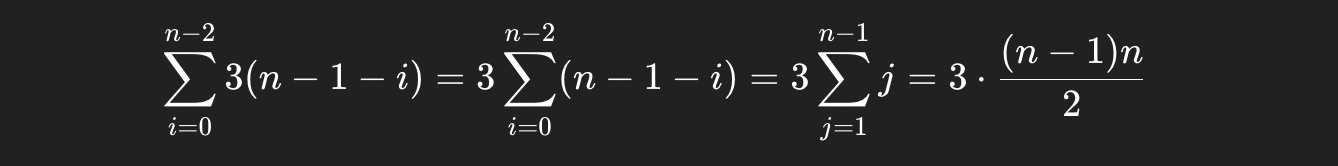
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定,可用于链式结构
快速排序:
左 <= 基准arr[ left ] <= 右
优化快速排序——基准数优化:
在数组中选取三个候选元素(通常为数组的首、尾、中点元素), 并将这三个候选元素的中位数作为基准数 。
时间复杂度为 O( n log2 (n) )
最坏情况(有序序列):O( n^2 ),变成了冒泡排序
空间复杂度为 O( log2 (n) )
非稳定排序
简单选择排序:
每轮在区间 [n,length−1] 中找到最小值,放在首位arr[ n ]处
n是当前的轮数,n从0到 length-1
时间复杂度为 O(n^2)
空间复杂度为 O(1)
非稳定排序(如果要实现稳定的话,元素应该逐个向后移动)
所有排序的总结:

静态排序:冒泡排序、选择排序
动态排序:插入排序、快速排序

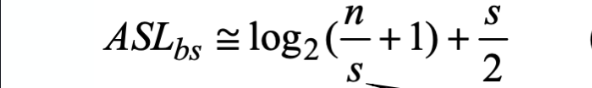

 浙公网安备 33010602011771号
浙公网安备 33010602011771号