图
github仓库:https://github.com/EanoJiang/Data-structures-and-algorithms
图最主要解决的是路径寻找问题
图的基本概念
定义
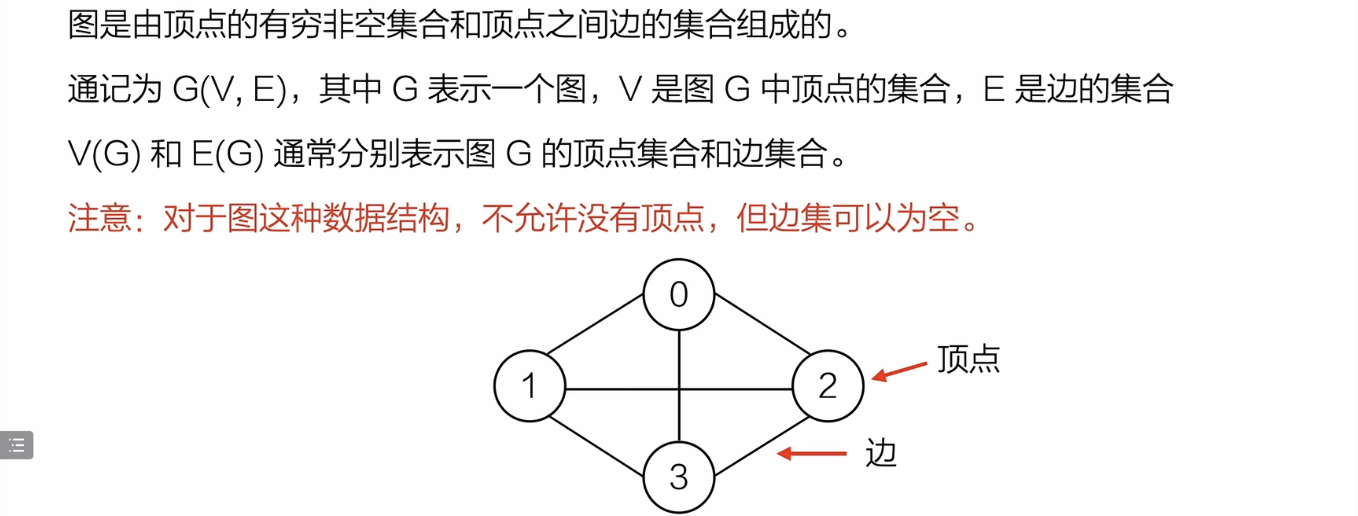
图G:graph 顶点V:vertex 边E:edge
图的分类
有向图和无向图
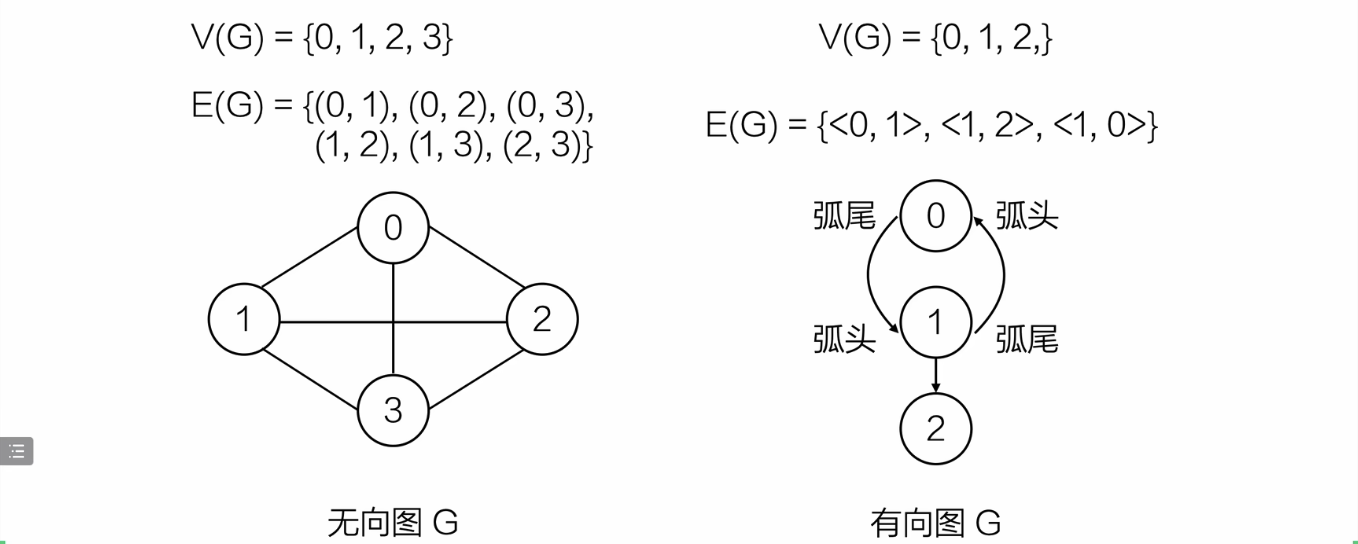
简单图和多重图
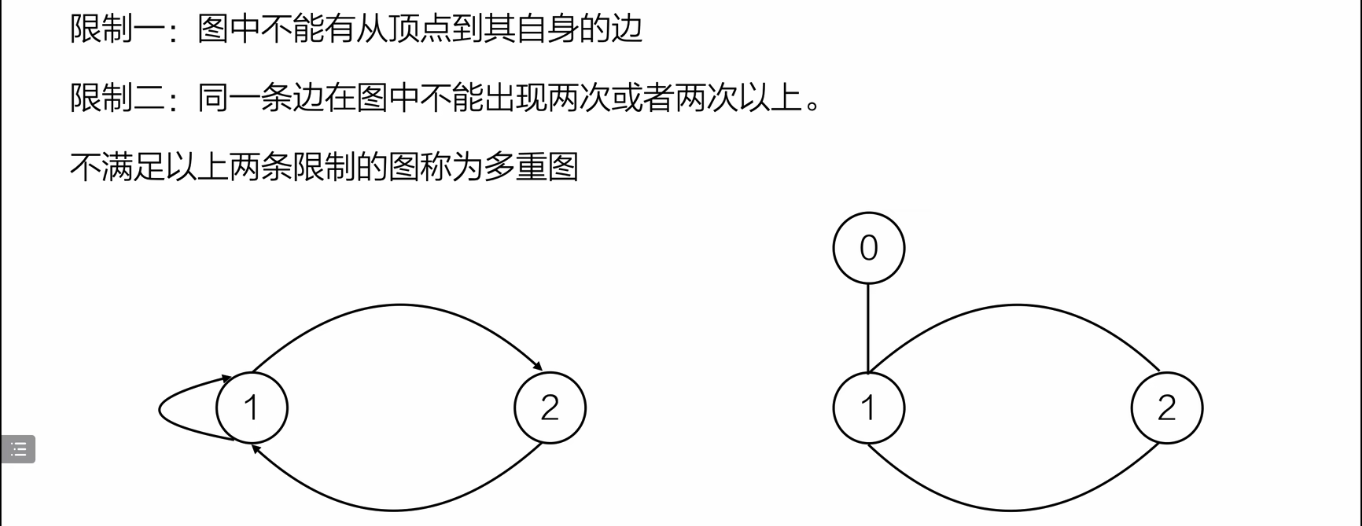
图二不满足限制二,因为从无向图的逻辑看来:1和2之间有两条一样的边
本质:简单图其实就是不能有自环和重边
完全图
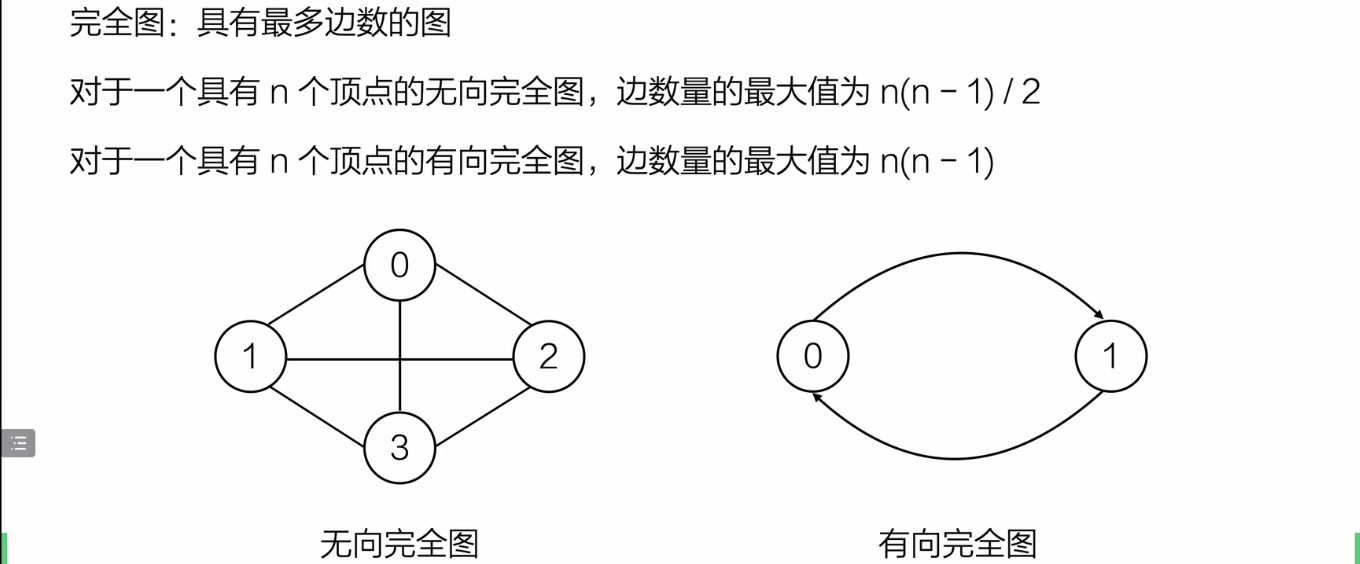
无向图的最大边数:C(n,2)=n(n-1)/2
有向图最大边数 = 无向图最大边数*2
路径和路径长度

和树一样,路径长度就是路径上有几条边
路径举例
0到1的路径:
- {0,3,1} 路径长度为2
- {0,2,3,1} 路径长度为3
简单路径和简单回路

简单路径就是没有重复的顶点
简单回路就是除了首尾重复,其他顶点不能重复
简单路径举例

顶点的度
度:对于无向图来说,与顶点相关联的边数
入度:对于有向图来说,指向该顶点的边数
出度:对于有向图来说,从该顶点出发的边数
度与边的关系
无向图:所有顶点的度数之和 = 边数 * 2
有向图:入度之和 = 出度之和 弧头数之和 = 弧尾数之和
子图
就是子集
连通和连通图
连通:无向图中,两个顶点之间有路径,那这两个顶点就是连通的
连通图:图的任意两个顶点都连通,就是连通图
注意:有路径就是连通的,没说必须是直接连线!!!
举例说明
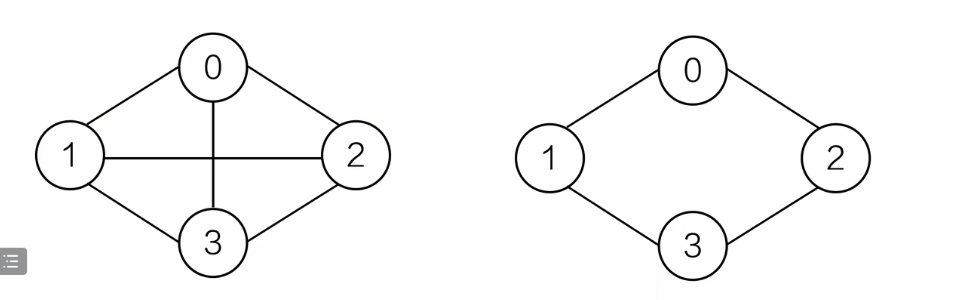
图一是连通图,图二也是连通图
连通分量
这是对于无向图的一个概念
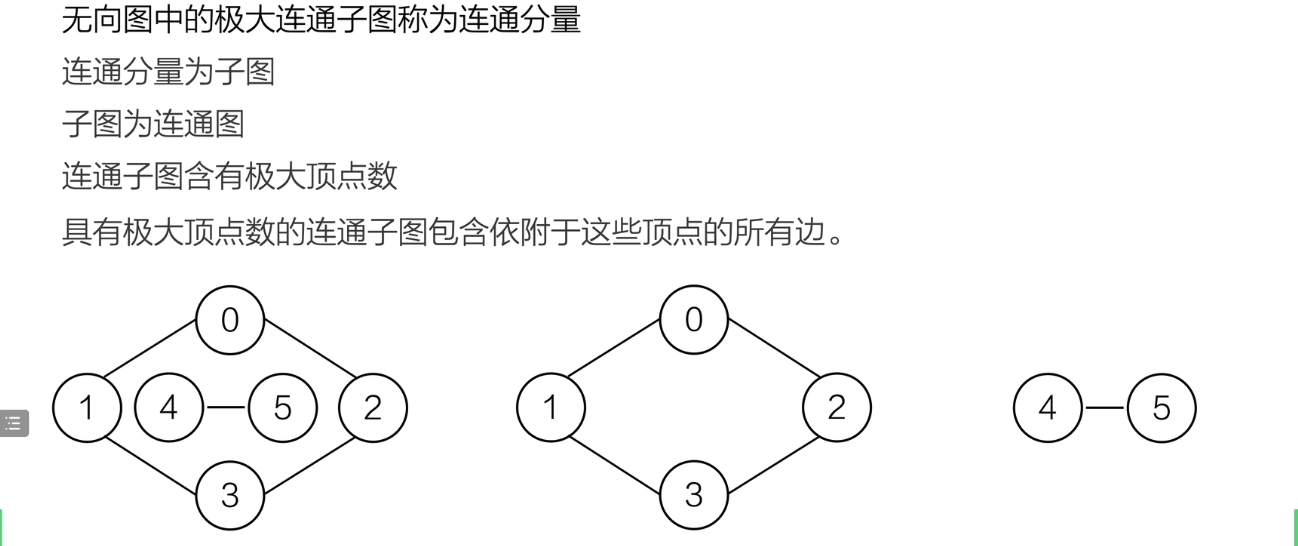
图二是图一的连通分量
连通分量其实就是一个无向图的连通的子图中,顶点数最多的一个。
强连通图

强连通图是对于有向图而言的,他的每两个顶点来回都有路径,那就是强连通图。
举例说明
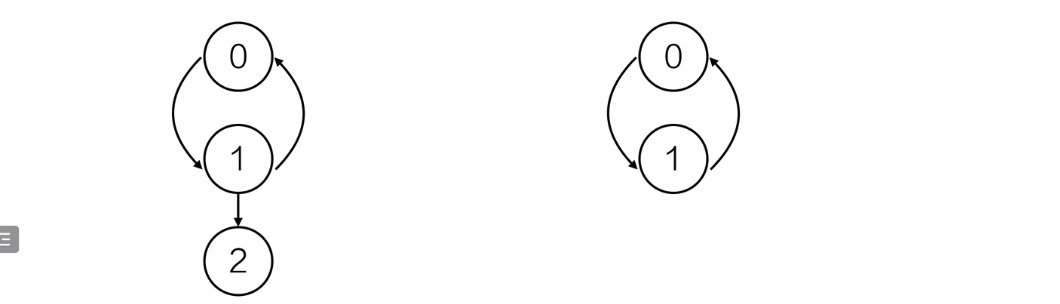
图一不是强连通图,因为1->2,但是没有2->1
图二是强连通图
强连通分量
就是有向图里的连通分量:一个有向图,他的强连通的子图中,顶点数最多的一个。
举例说明
比如上面那个图,图二就是图一的强连通分量
注意:(强)连通分量不需要原图也是(强)连通图,只需要保证他的子图是(强)连通图就行,再找出这个(强)连通子图的顶点数最多的一个。
生成树

生成树的顶点数n,边数为n-1
举例说明
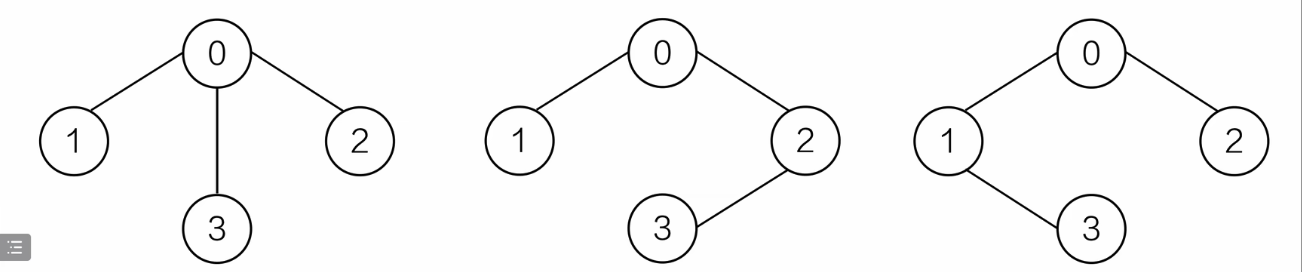
四个顶点,三条边
权值网和带权图
权值网:边的权值
带权图:边上带权值的图
比如下面的带权图:
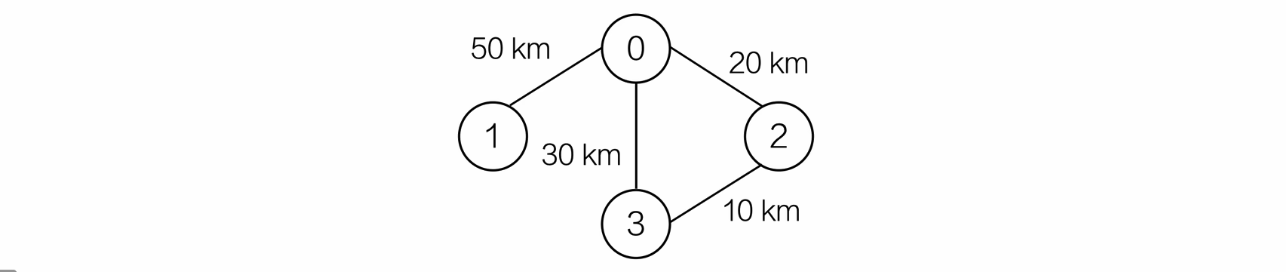
习题

无向连通图有个性质:所有顶点的度数之和 = 边数 * 2
那肯定是偶数,1️⃣正确
2️⃣可以举出反例:
1
/ \
2 3
这是一个无向连通图,每两个顶点之间都有路径,边数2 ,顶点数3,2️⃣不满足
3️⃣更不一定了,随便画个环就是反例
所以选A

首先要保证6个顶点的无向图时候是无向完全图,也就是最大的边数C(n,2) = n(n-1)/2 = 15。
这时候我再加一个顶点,这个顶点怎么与这6个点连线都肯定是连通的。
这样就满足了在这个边数下,我怎么画无向图都是连通的。
这样最少的边数就是15+1 = 16,选C

图和树一样:顶点总数n = n0 + n1 + n2 + n3 + n4 = n0 + n1 + n2 + 4 + 3
所有顶点的度数之和 = 边数 * 2
也就是,n1 + 2n2 + 3n3 + 4n4 = 16 * 2
等价于,n1 + 2n2 + 3 * 4 + 4 * 3 = 32
等价于,n1 + 2n2 = 8
n1 + 2n2 = 8 式中,n1的系数是1,n2的系数是2,要使顶点总数n最小,那剩下的度就只能有2,所以度1和度0都不存在
如上的分析也可以根据 n1 + 2n2 = 8 穷举出所有情况,找出最小的总和n即可
这样算得,n2 = 4
n = 4+4+3 = 11
选B
图的存储和遍历
图的存储结构
邻接矩阵——数组
无向图的邻接矩阵是对称矩阵
有向图的邻接矩阵需要看起点和终点,所以不是对称矩阵
无向图的邻接矩阵
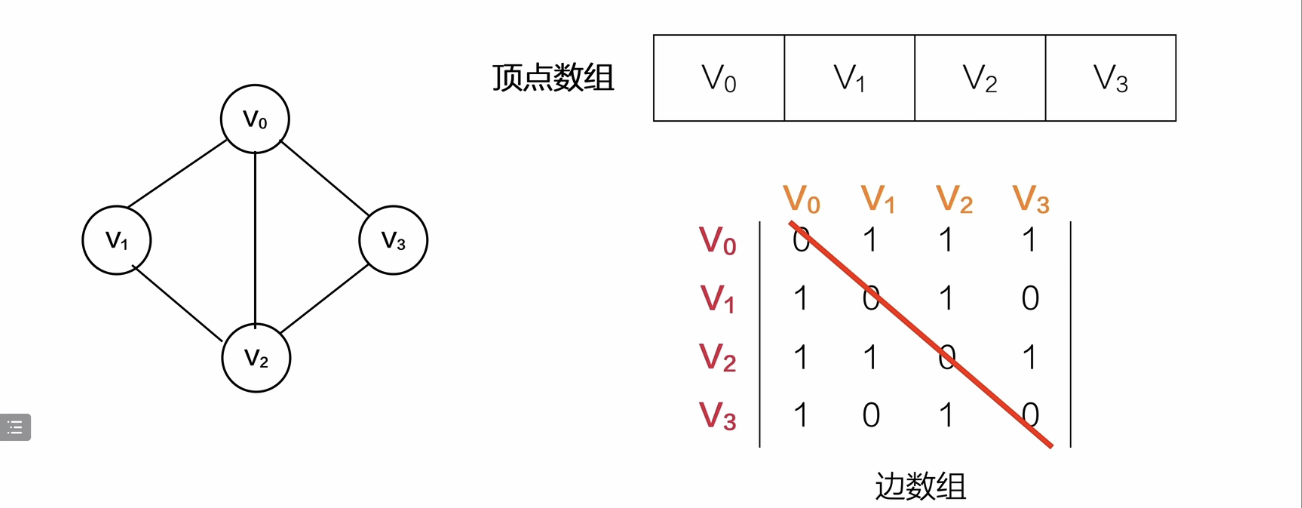
所以对于无向图的邻接矩阵,可以只列出上半部分的矩阵,然后复制给下半部分的:
双层循环:a[j][i] = a[i][j]
有向图的邻接矩阵
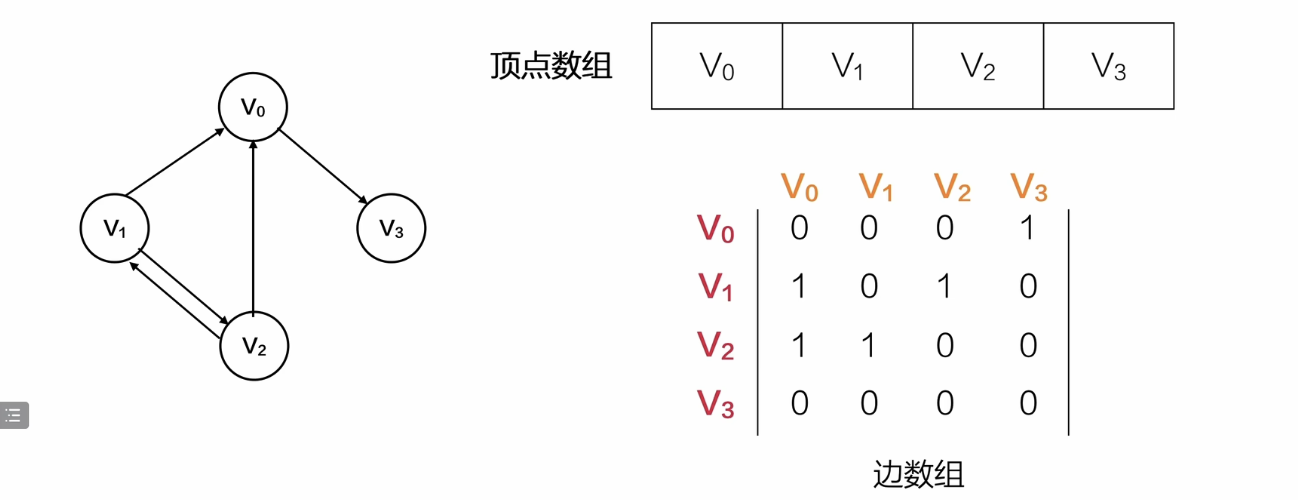
红色(纵)是起点,黄色(横)是终点
红色(纵) -> 黄色(横) 出度
黄色(横) -> 红色(纵) 入度
带权值的邻接矩阵
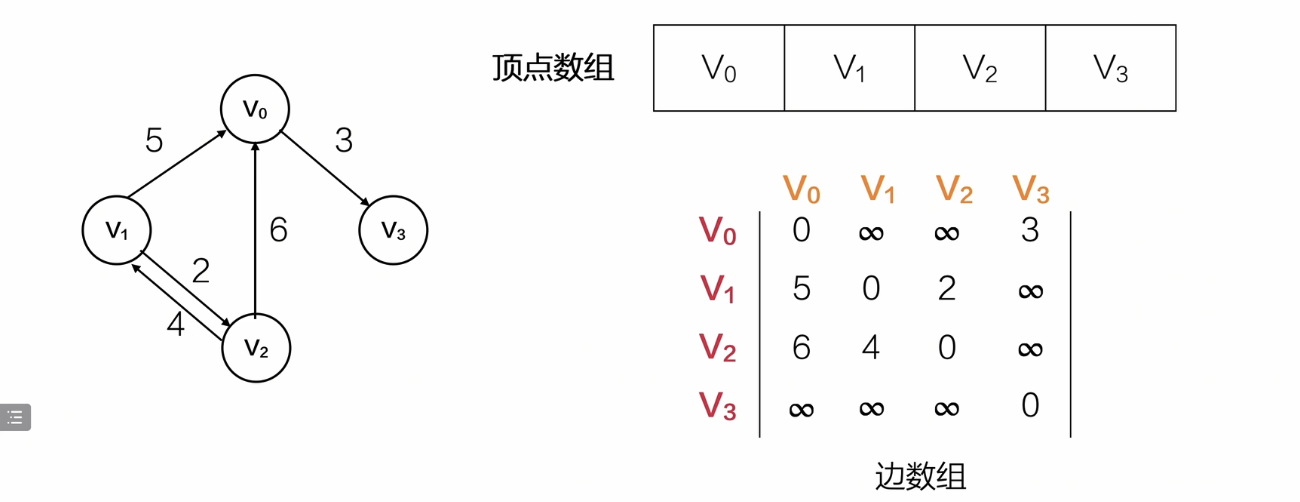
邻接表——链表
无向邻接表
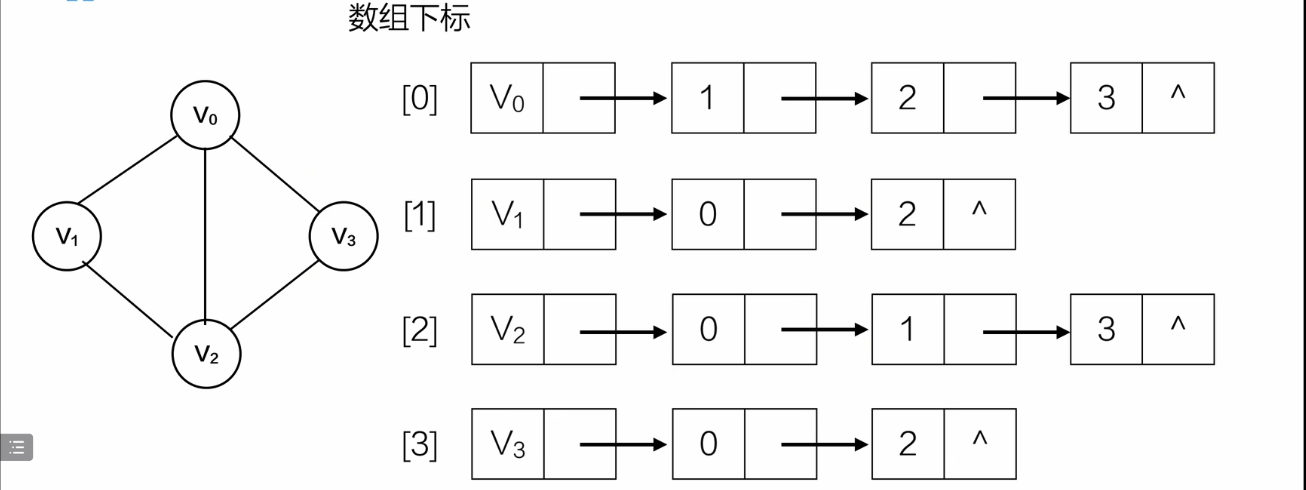
后面的顺序无关,只是代表V0和 数组下标123的头节点(顶点)的链表 直接相连。
有向邻接表
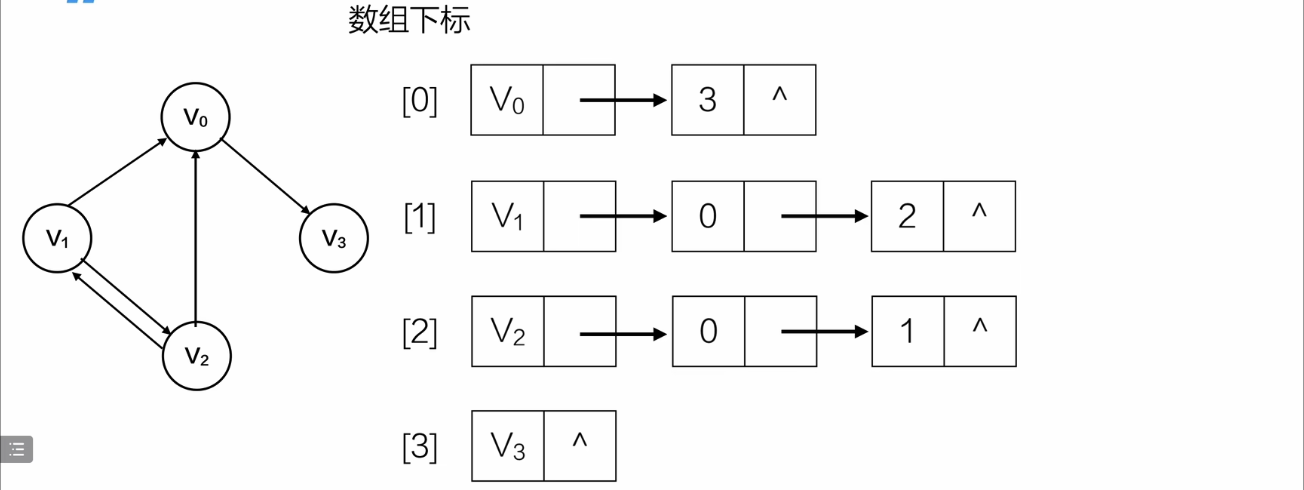
这是只表示出度的有向邻接表
有向逆邻接表——入度
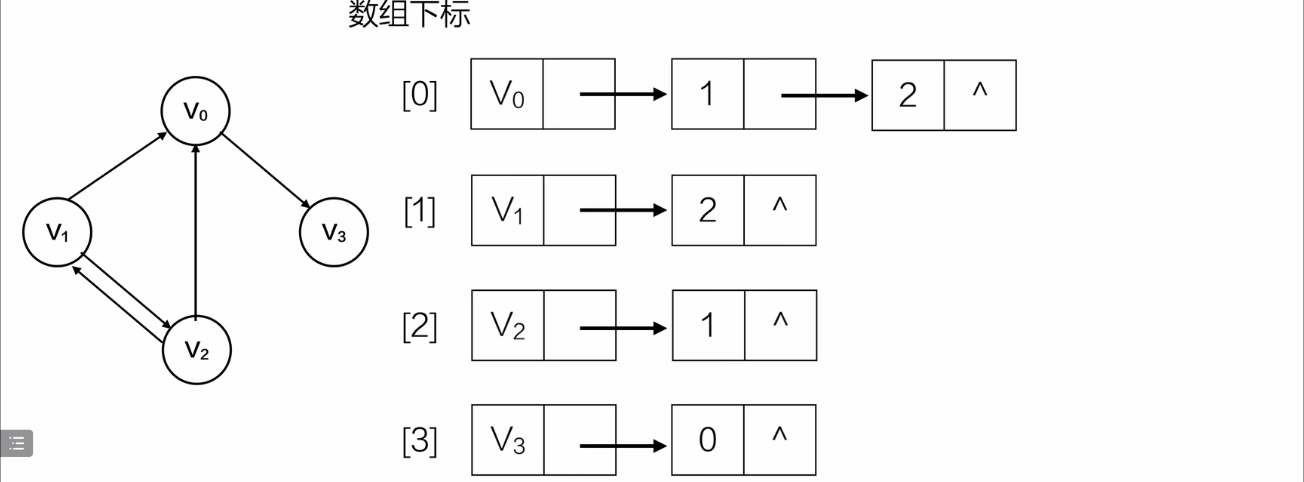
带权值的邻接表
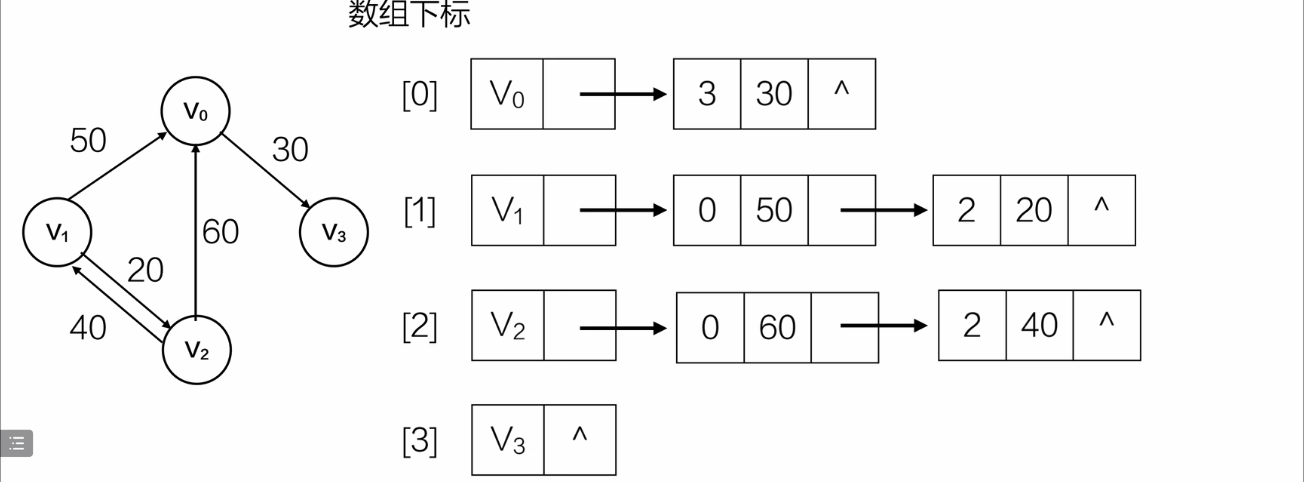
十字链表
整合了有向邻接表和有向逆邻接表
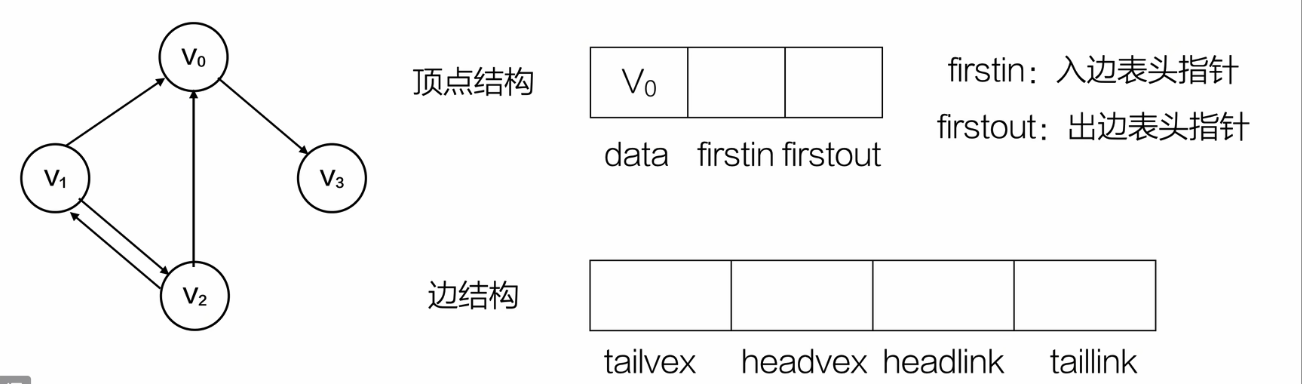
橙色虚线是V0的入边链表
V0的入边指针指向出边10的弧尾0,指向出边20的弧尾0
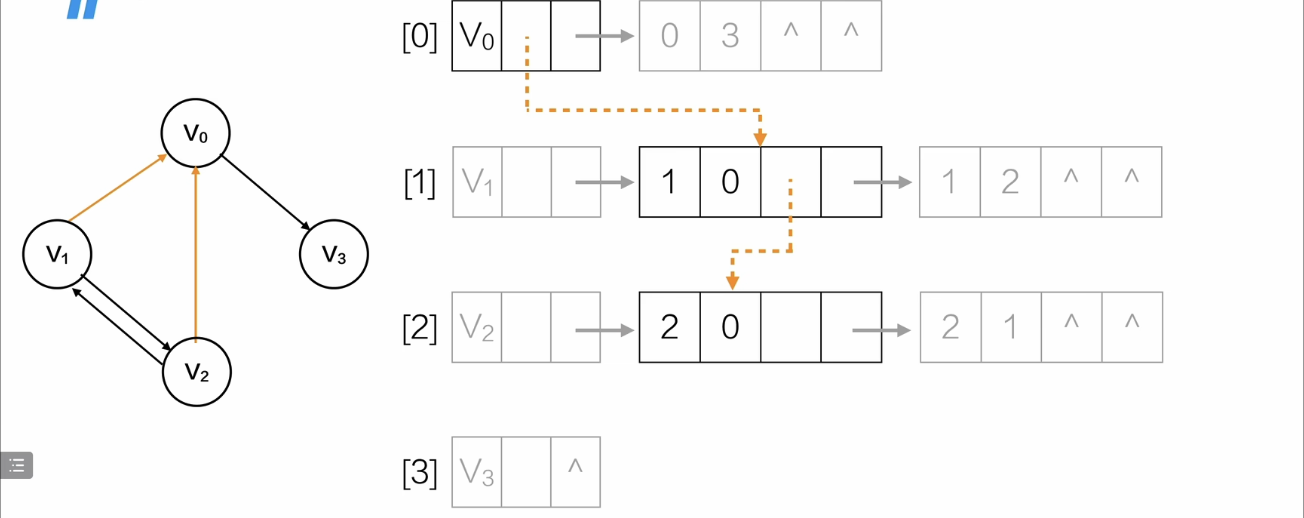
相当于,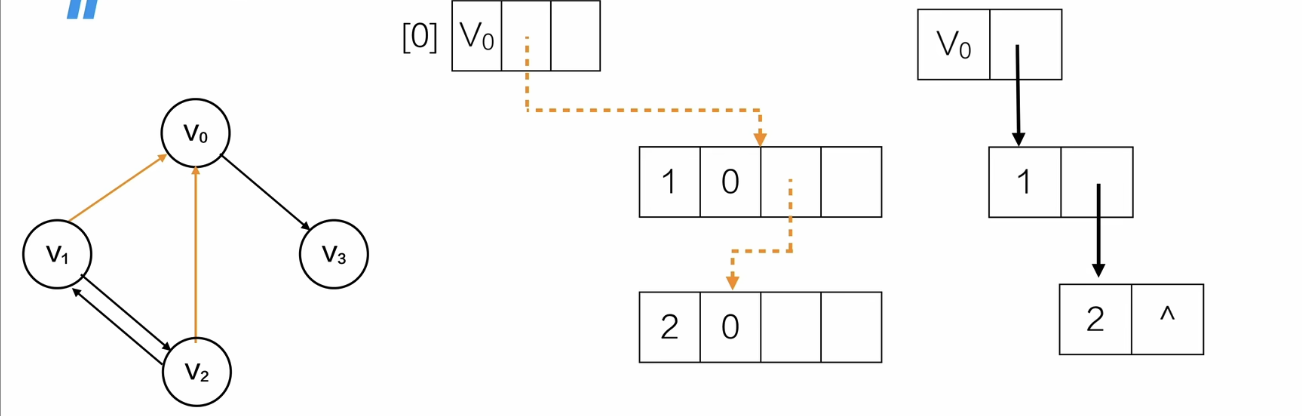
同样的方法画出剩余顶点的入边链表,
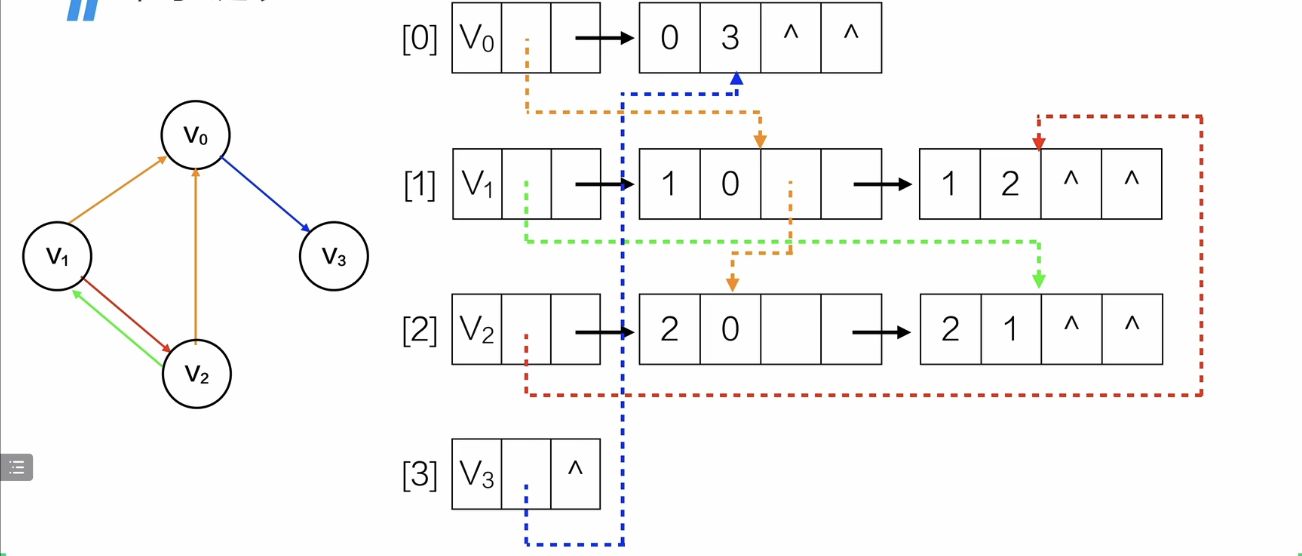
对于无向邻接表的链表结点空间浪费怎么解决呢?
邻接多重表

实例(有点抽象)
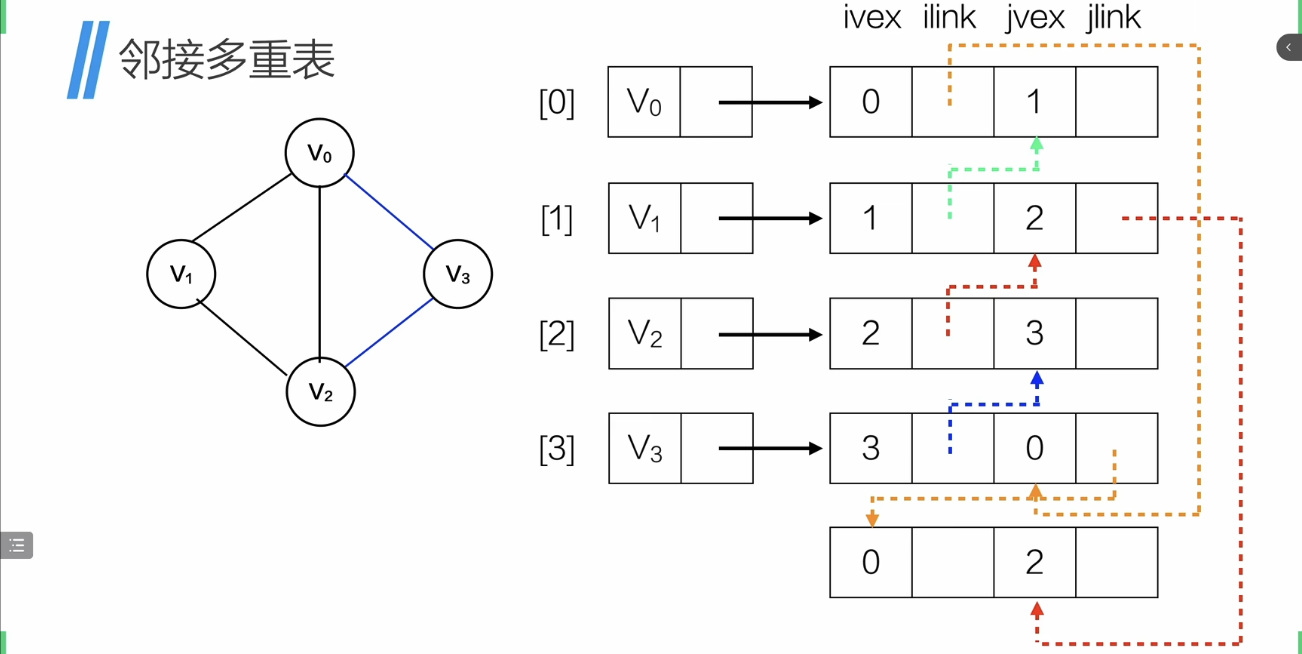
DFS和BFS
DFS(Depth-First Search 深度优先遍历)
一直向下挖,挖不动了就移动到同层然后继续向下挖
其实就是前序遍历
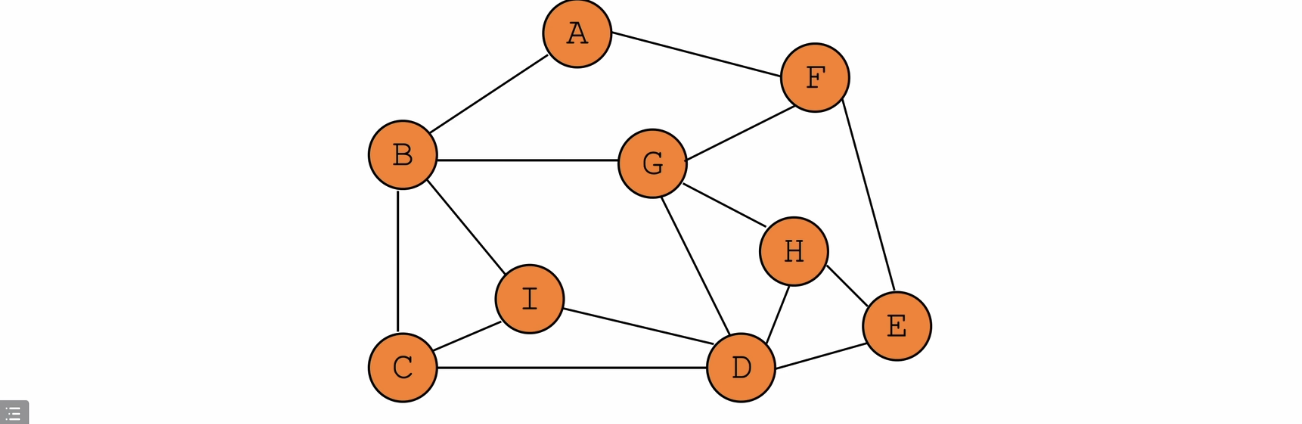
实例:从A开始遍历全部顶点
-
先沿着左边一条路走到黑
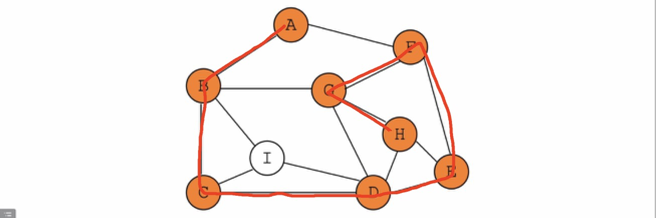
-
找不到,开始原路返回(蓝色路径),然后移到同层继续向下找(红色路径)
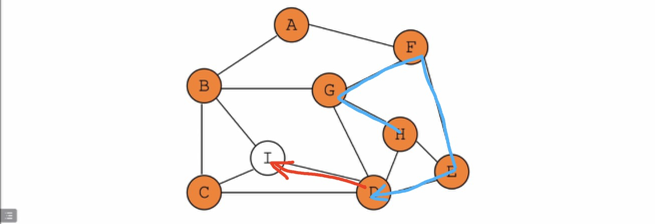
代码实现
- 先创建无向邻接矩阵
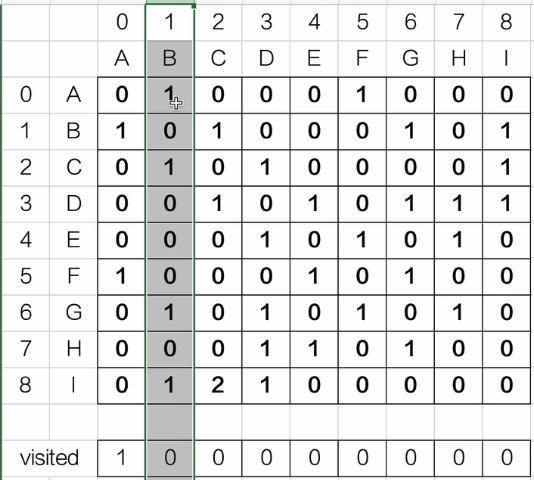
#include <stdio.h>
//顶点
typedef char VertexType;
//边
typedef int EdgeType;
#define MAXSIZE 100
//邻接矩阵
typedef struct Matrix_Graph
{
//顶点数组
VertexType vertex[MAXSIZE];
//边数组
EdgeType arc[MAXSIZE][MAXSIZE];
//顶点数
int vertex_num;
//边数
int edge_num;
}Matrix_Graph;
//创建图
void create_graph(Matrix_Graph* G)
{
G->vertex_num = 9;
G->edge_num = 15;
G->vertex[0] = 'A';
G->vertex[1] = 'B';
G->vertex[2] = 'C';
G->vertex[3] = 'D';
G->vertex[4] = 'E';
G->vertex[5] = 'F';
G->vertex[6] = 'G';
G->vertex[7] = 'H';
G->vertex[8] = 'I';
for (int i = 0; i < G->vertex_num; i++)
{
for (int j = 0; j < G->vertex_num; j++)
{
G->arc[i][j] = 0;
}
}
/*连线*/
//A-B A-F
G->arc[0][1] = 1;
G->arc[0][5] = 1;
//B-C B-G B-I
G->arc[1][2] = 1;
G->arc[1][6] = 1;
G->arc[1][8] = 1;
//C-D C-I
G->arc[2][3] = 1;
G->arc[2][8] = 1;
//D-E D-G D-H D-I
G->arc[3][4] = 1;
G->arc[3][6] = 1;
G->arc[3][7] = 1;
G->arc[3][8] = 1;
//E-F E-H
G->arc[4][5] = 1;
G->arc[4][7] = 1;
//F-G
G->arc[5][6] = 1;
//G-H
G->arc[6][7] = 1;
//无向图,所以直接把出边的值斜对角对称赋值给入边
for (int i = 0; i < G->vertex_num; i++)
{
for (int j = 0; j < G->vertex_num; j++)
{
G->arc[j][i] = G->arc[i][j];
}
}
}#include <stdio.h>
//顶点
typedef char VertexType;
//边
typedef int EdgeType;
#define MAXSIZE 100
//邻接矩阵
typedef struct Matrix_Graph
{
//顶点数组
VertexType vertex[MAXSIZE];
//边数组
EdgeType arc[MAXSIZE][MAXSIZE];
//顶点数
int vertex_num;
//边数
int edge_num;
}Matrix_Graph;
//创建图
void create_graph(Matrix_Graph* G)
{
G->vertex_num = 9;
G->edge_num = 15;
G->vertex[0] = 'A';
G->vertex[1] = 'B';
G->vertex[2] = 'C';
G->vertex[3] = 'D';
G->vertex[4] = 'E';
G->vertex[5] = 'F';
G->vertex[6] = 'G';
G->vertex[7] = 'H';
G->vertex[8] = 'I';
for (int i = 0; i < G->vertex_num; i++)
{
for (int j = 0; j < G->vertex_num; j++)
{
G->arc[i][j] = 0;
}
}
/*连线*/
//A-B A-F
G->arc[0][1] = 1;
G->arc[0][5] = 1;
//B-C B-G B-I
G->arc[1][2] = 1;
G->arc[1][6] = 1;
G->arc[1][8] = 1;
//C-D C-I
G->arc[2][3] = 1;
G->arc[2][8] = 1;
//D-E D-G D-H D-I
G->arc[3][4] = 1;
G->arc[3][6] = 1;
G->arc[3][7] = 1;
G->arc[3][8] = 1;
//E-F E-H
G->arc[4][5] = 1;
G->arc[4][7] = 1;
//F-G
G->arc[5][6] = 1;
//G-H
G->arc[6][7] = 1;
//无向图,所以直接把出边的值斜对角对称赋值给入边
for (int i = 0; i < G->vertex_num; i++)
{
for (int j = 0; j < G->vertex_num; j++)
{
G->arc[j][i] = G->arc[i][j];
}
}
}
- DFS
//标志位数组:用来标记某个顶点是否已经遍历过
int visited[MAXSIZE];
void dfs(Matrix_Graph G, int i)
{
visited[i] = 1;
printf("%c\n", G.vertex[i]);
for (int j = 0; j < G.vertex_num; j++)
{
if (G.arc[i][j] == 1 && visited[j] == 0)
{
//递归,把未遍历过的下一个顶点作为参数传入
dfs(G, j);
}
}
}
int main(int argc, char const *argv[])
{
Matrix_Graph G;
create_graph(&G);
//初始化标志位数组
for (int i = 0; i < G.vertex_num; i++)
{
visited[i] = 0;
}
dfs(G, 0);
return 0;
}//标志位数组:用来标记某个顶点是否已经遍历过
int visited[MAXSIZE];
void dfs(Matrix_Graph G, int i)
{
visited[i] = 1;
printf("%c\n", G.vertex[i]);
for (int j = 0; j < G.vertex_num; j++)
{
if (G.arc[i][j] == 1 && visited[j] == 0)
{
//递归,把未遍历过的下一个顶点作为参数传入
dfs(G, j);
}
}
}
int main(int argc, char const *argv[])
{
Matrix_Graph G;
create_graph(&G);
//初始化标志位数组
for (int i = 0; i < G.vertex_num; i++)
{
visited[i] = 0;
}
dfs(G, 0);
return 0;
}
BFS(Breadth-First Search 广度优先遍历)
同层先挖完,再向下挖
其实就是层序遍历(我还没学)
实例:从A开始遍历所有顶点
-
遍历所有同层顶点
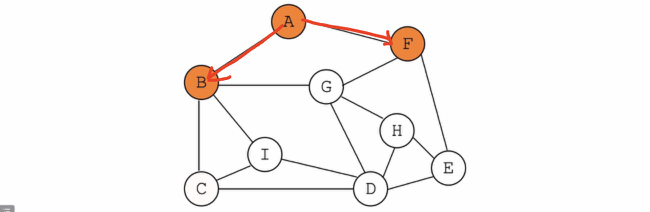
-
遍历下一层顶点
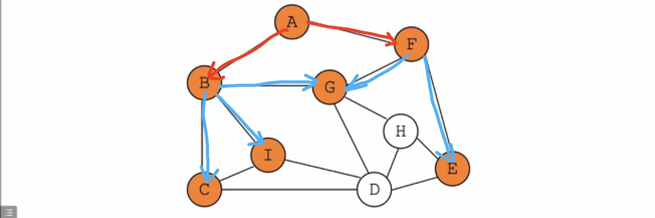
代码实现
创建无向邻接矩阵与前面的相同
BFS:
int visited[MAXSIZE];
int front = 0;
int rear = 0;
int queue[MAXSIZE];
void bfs(Mat_Grph G)
{
int i = 0;
visited[i] = 1;
printf("%c\n", G.vertex[i]);
//当前顶点入队
queue[rear] = i;
rear++;
//队列不空,就循环
//也就是只有访问完了这一层的所有顶点,才会进入下一层————这是BFS的关键
while(front != rear)
{
//队头出队
i = queue[front];
front++;
//遍历当前层的所有顶点
for (int j = 0; j < G.vertex_num; j++)
{
if (G.arc[i][j] == 1 && visited[j] == 0)
{
visited[j] = 1;
printf("%c\n", G.vertex[j]);
queue[rear] = j;
rear++;
}
}
}
}
int main(int argc, char const *argv[])
{
Mat_Grph G;
create_graph(&G);
for (int i = 0; i < G.vertex_num; i++)
{
visited[i] = 0;
}
bfs(G);
return 0;
}
最小生成树(Prim)
考完这个逼试我再来学👹


 浙公网安备 33010602011771号
浙公网安备 33010602011771号