时间复杂度

> github仓库：https://github.com/EanoJiang/Data-structures-and-algorithms

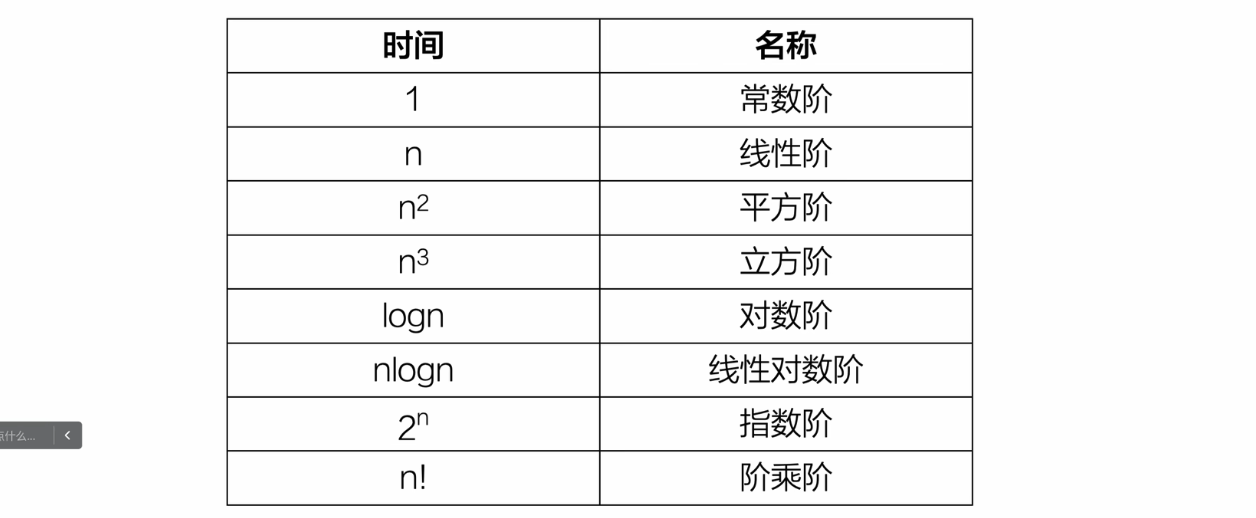
复杂度 详解

常数阶

线性阶

平方阶

立方阶

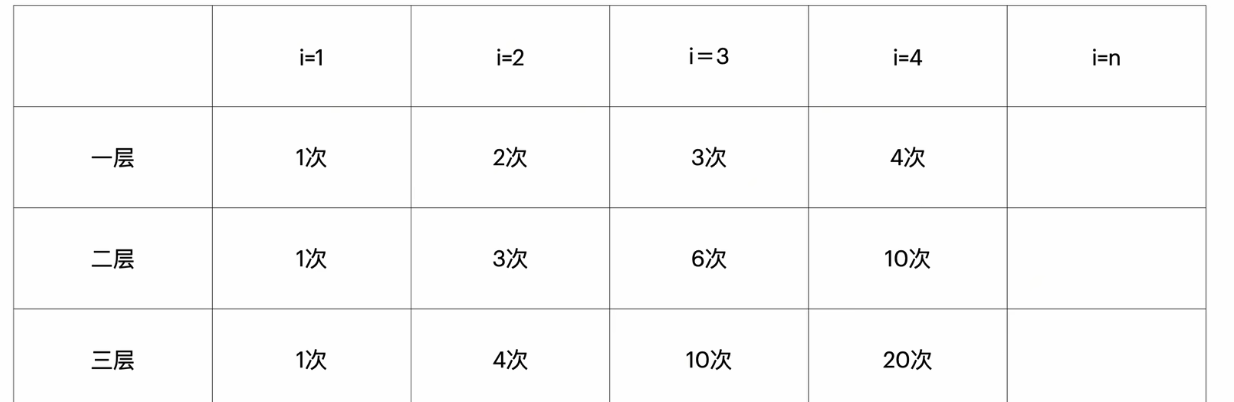
分析： i = n的时候，第二层执行n次，所以第二层从一开始累加到n

可以画出如下的表格来分析：

对数阶

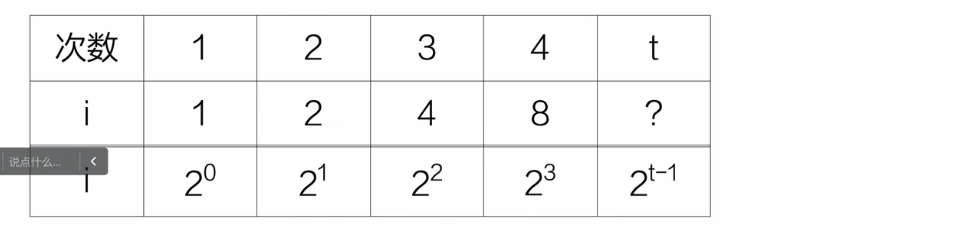
结束条件：2^(t-1) = n 👉 t = log2(n) + 1

所以时间复杂度就是O( log2(n) )

---

实战环节

结束条件：x = 2^(t-1) = n/2 ，也就是t = log2(n) 的时间复杂度，选A

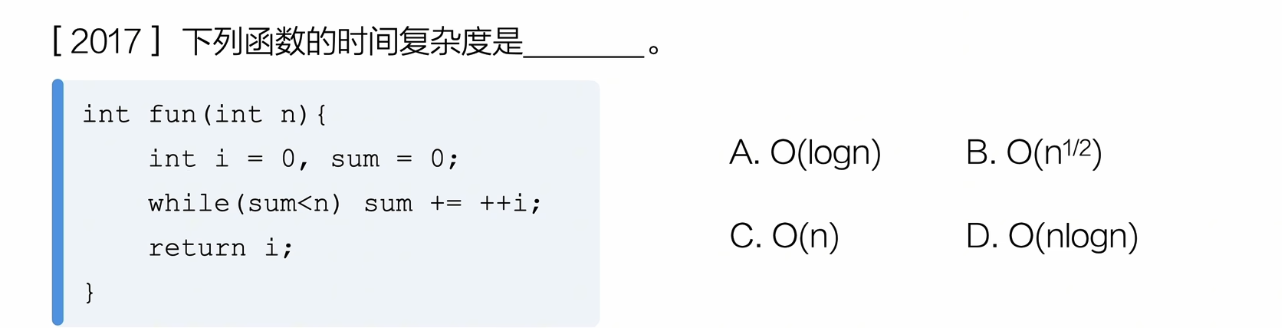
结束条件：sum = t*(t+1)/2 = n ，也就是 t = 根号n 的时间复杂度，选B

次数	1	2	t
i	1	2	t
sum	1	3	1+2+..+t

结束条件：n = (t+1)^2 ，也就是t = 根号n 的复杂度，选B

次数	1	2	t
x	1	2	t
(x+1)(x+1)	(1+1)^2	(2+1)^2	(t+1)^2

实际上就是x每次自增，结束条件是n = (x+1)^2

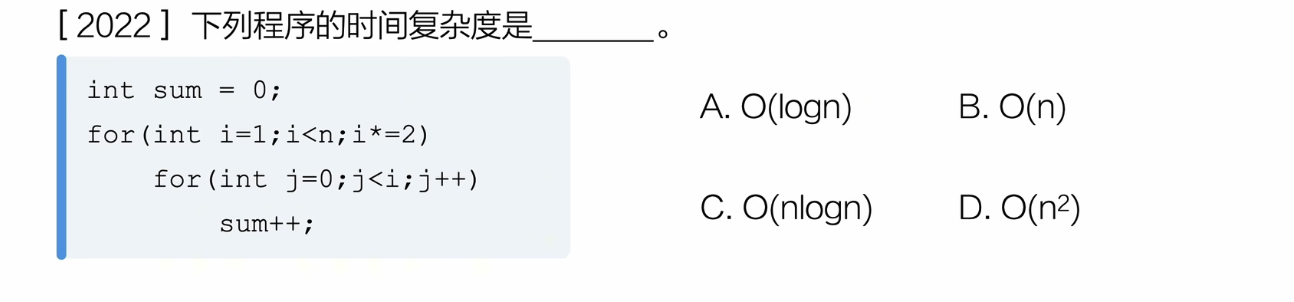
复杂度分析：

第一层	2^(t-1) = n	log2(n)

次数	1	2	t
i	2^0	2^1	2^(t-1)
内层执行的次数	2^0	2^1	2^(t-1)

内层总共执行次数是累加第二行的结果，

所以时间复杂度是t = 2^0 + 2^1 + .. + 2^(log2(n)-1) = 2^0 + 2^1 + .. + 2^log2(n) = 1*(1-2^log2(n))/(1-2) = n-1 = n

所以，

第二层	n

最终复杂度以最大的为准， 也就是O(n)，选B