Hello 算法——只是开胃菜

1. 初识算法

1.1 二分查找：查字典

1.2 插入排序：整理扑克牌（处理小型数据集时非常高效）

1.3 贪心算法：货币找零（每一步都采取当前看来最好的选择）

2. (渐进)复杂度分析（asymptotic complexity analysis）

2.1 算法效率评估：两个维度 ➡ time 、 space

2.2 迭代与递归

2.2.1 迭代（iteration）

// for循环：适用于在预先知道迭代次数的情况下

eg：1 + 2 + … + n

int ForLoop(int n)
{
  int res = 0;
  for (int i = 1; i <= n; i++)
  //for循环中 ++i和 i++ 是等价的
  {
    res += i;
  }
  return res;
}

这样的求和函数的操作数量与输入数据大小 n 成正比，或者说成“线性关系”。

// while循环

int WhileLoop(int n)
{
  int res = 0;
  int i = 1;
  while (i <= n)
  {
    res += i;
    i++;
  }
  return res;
}

**while** 循环比 **for**循环的自由度更高，可自由设计更新条件

但是可以看出，**for** 循环的代码更加紧凑，**while** 循环更加灵活

// 嵌套循环

char *nestedForLoop(int n) {
    // n * n 为对应点数量，"(i, j), " 对应字符串长最大为 6+1*2，加上最后一个空字符 \0 的额外空间
    //6 是固定部分的长度，包括 "("、", " 和 "), " 这些字符
    //假设i和j都是一位数字
    int size = n * n * 8 + 1;
    char *res = malloc(size*sizeof(char));
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            char tmp[8];
            snprintf(tmp, 8, "(%d, %d), ", i, j);
            strncat(res, tmp, size-strlen(res)-1);
        }
    }
    return res;
}

操作数量与 n 成平方关系

2.2.2 递归（recursion）

递：程序不断深入地调用自身，直到达到“终止条件”。

归：触发“终止条件”后，从最深层开始逐层返回，汇聚每一层的结果。

// 递归
int recur(int n){
    if (n == 1) 
        return 1;
    int fn = recur(n-1) + n;
    return fn;
}

两种操作方式的区别：

//尾递归（tail recursion）

同样还是求和问题：

// 尾递归函数
int TailRecur(int n, int res){
    if (n == 0)
        return res;
    return TailRecur(n - 1, n + res);
}

//递归树

// 递归树，斐波那契数列
int fib(int n){
    // 递归终止条件:前两项
    if(n == 1 || n == 2)
        return n-1;
    int fn = fib(n-1) + fib(n-2);
    return fn;
}

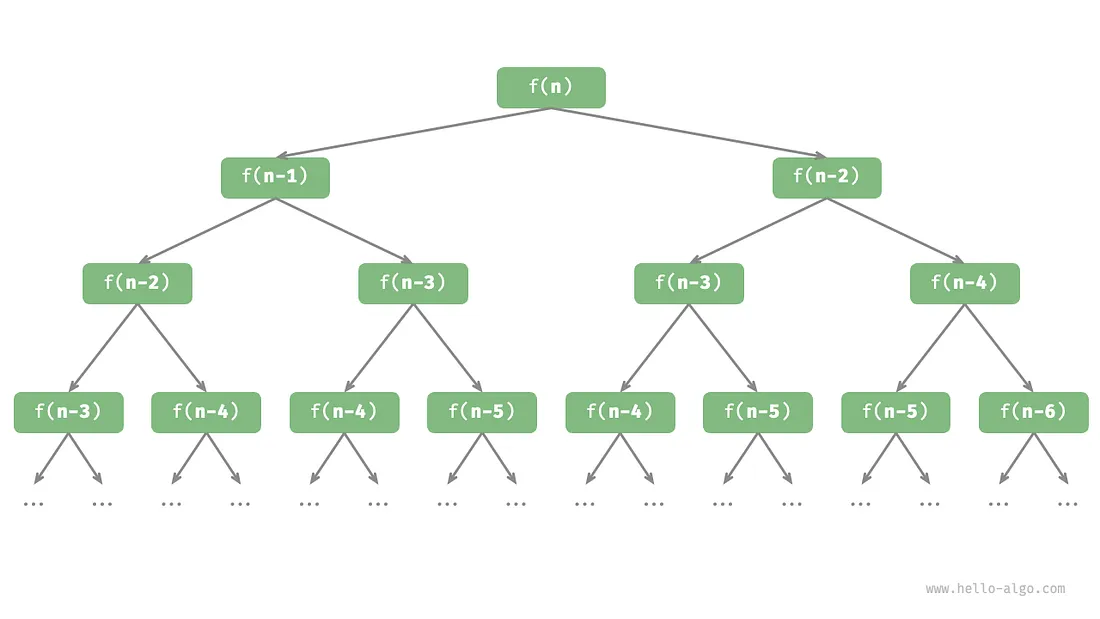
从本质上看，递归体现了“将问题分解为更小子问题”的思维范式，这种分治策略至关重要。

从算法角度看，搜索、排序、回溯、分治、动态规划等许多重要算法策略直接或间接地应用了这种思维方式。
从数据结构角度看，递归天然适合处理链表、树和图的相关问题，因为它们非常适合用分治思想进行分析。

// 栈

/* 使用迭代模拟递归 */
int forLoopRecur(int n) {
    //栈
    int stack[100];
    //栈顶索引
    int topStack = -1;
    //入栈:索引从栈顶向上
    for(int i = n; i > 0; i--){
        stack[1 + topStack++] = i;
    }
    //入栈操作全部完成后，栈顶在最上面
    //出栈：索引从栈顶向下
    int res = 0;
    while(topStack >= 0){
        res += stack[topStack--];
    }

    return res;
}

2.3 时间复杂度

2.3.1 统计时间增长趋势

2.3.2 函数渐进上界

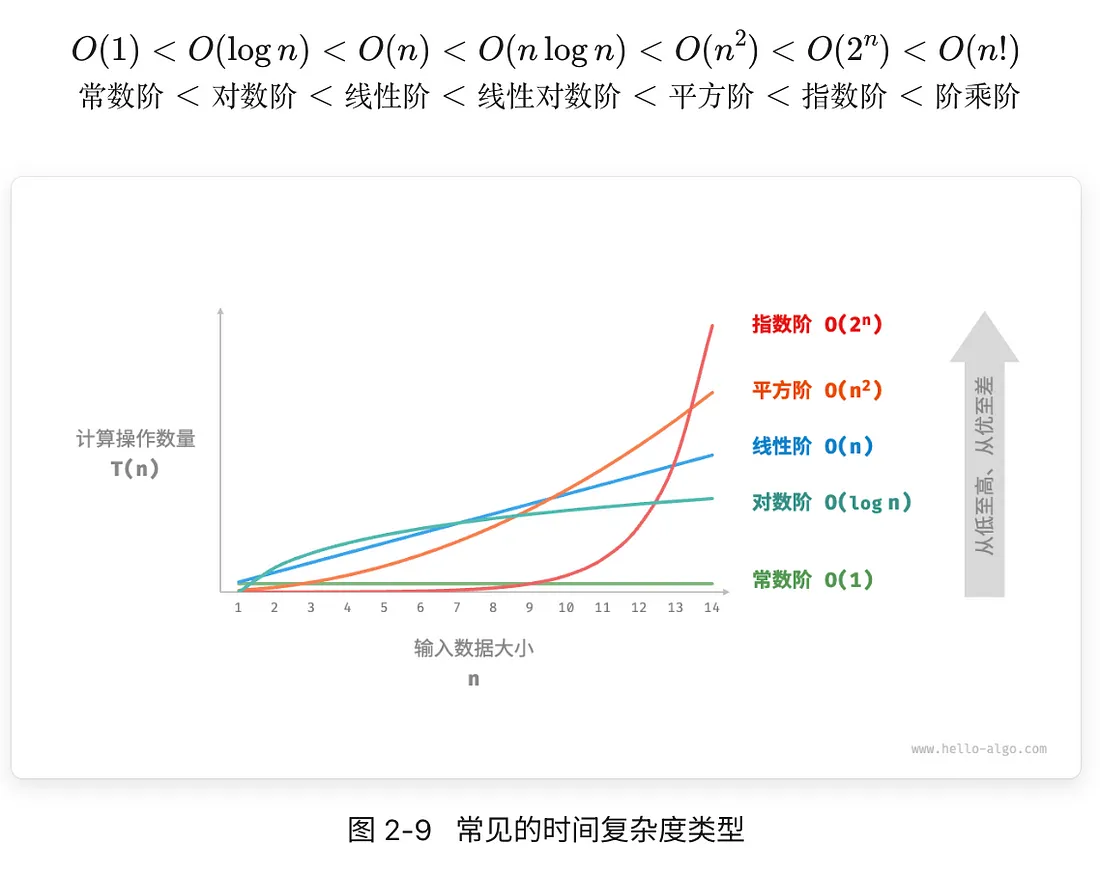
2.3.4 常见复杂度类型

1. 常数阶 O(1)

操作数量与输入数据大小 n 无关。

2. 线性阶O(n)

常出现在单层循环中。

3. 平方阶O(n²)

常出现在嵌套循环中。

eg:冒泡排序

//冒泡排序 操作数
int bubble(int *nums,int n){
    int count = 0;
    for (int i = n - 1; i >= 0; i--){
        for (int j = 0; j < i; j++){
            if (nums[j] > nums[j+1]){
                int temp = nums[j];
                nums[j] = nums[j+1];
                nums[j+1] = temp;
                //单层操作数为3
                count += 3;
            }
        }
    }
    return count;
}

指数阶 O(2^n)

2⁰ + 2¹ + … + 2^n

// 指数阶 循环实现
int Exponential(int n) {
    int count = 0;
    int bas = 1;
    // 每轮count=2^n，共n-1轮相加
    // 也就是2^0+2^1+2^2+...+2^(n-1)
    for (int i = 0; i < n; i ++){
        for (int j = 0; j < bas; j ++){
            count ++;
        }
        bas *= 2;     
    }
    return count;
}
// f(n) = 1 + 2^1 + 2^2 + ...+ 2^(n-1)
// 每次递归（子任务）：f(n) = 1 + 2f(n-1)       后面这些项每一项都是前一项的2倍
// 指数阶 递归实现
int ExponentialRecur(int n) {
    if (n == 1)
        return 1;
    int fn = 1 + 2 * ExponentialRecur(n - 1);
    return fn;
}

5. 对数阶O(log n)

与指数阶相反，对数阶反映了“每轮缩减到一半”的情况。设输入数据大小为 n ，由于每轮缩减到一半，因此循环次数是 log2⁡n ，即 2^n的反函数

// 对数阶 循环实现
// 对数阶：复杂度是对数阶

int logLoop(int n){
    int count = 0;
    while(n > 1){
        n /= 2;
        count++;
    }
    return count;
}
// 对数阶 递归实现

// f(n) = n/2 + n/4 + ... + 1
// 每次递归（子任务）：f(n) = n/2 + 1
int logRecur(int n)
{
    if (n <= 1){
        return 0;
    }
    return logRecur(n / 2) + 1;
}

6. 线性对数阶 O( nlog n )

常出现于嵌套循环中。

/* 线性对数阶 */

int linearLogRecur(int n) {
    if (n <= 1)
        return 1;
    //n + n/2 + n/4 +... + 1
    // 把第一次n 分解成两个子任务（二叉树），即为两个n/2开始的线性对数阶
    int count = linearLogRecur(n / 2) + linearLogRecur(n / 2);
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}

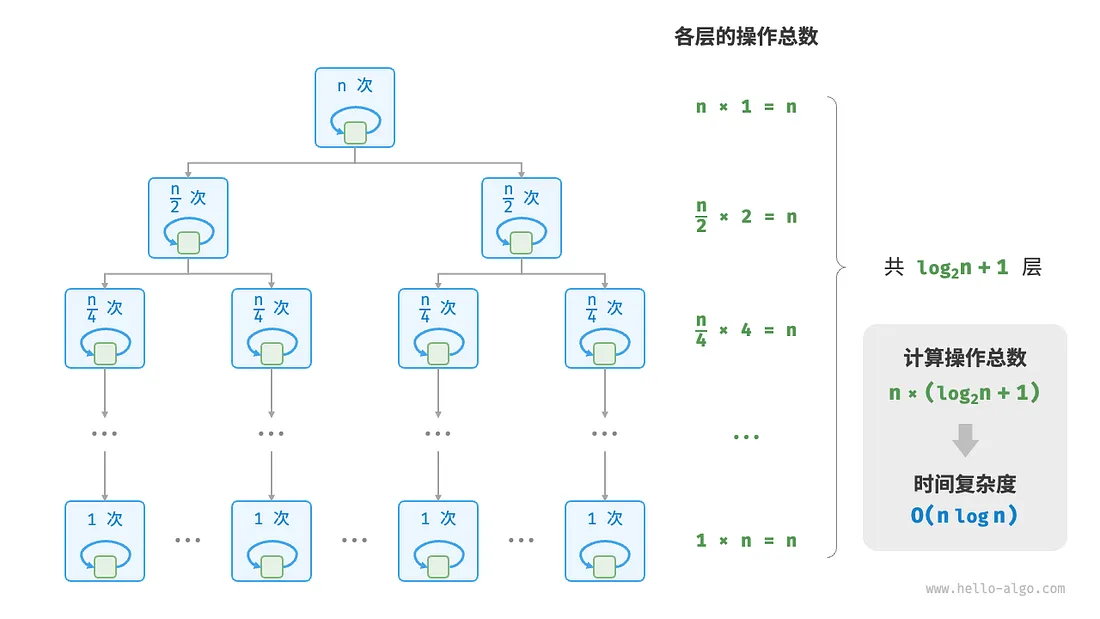
复杂度：n*(log2(n) + 1)

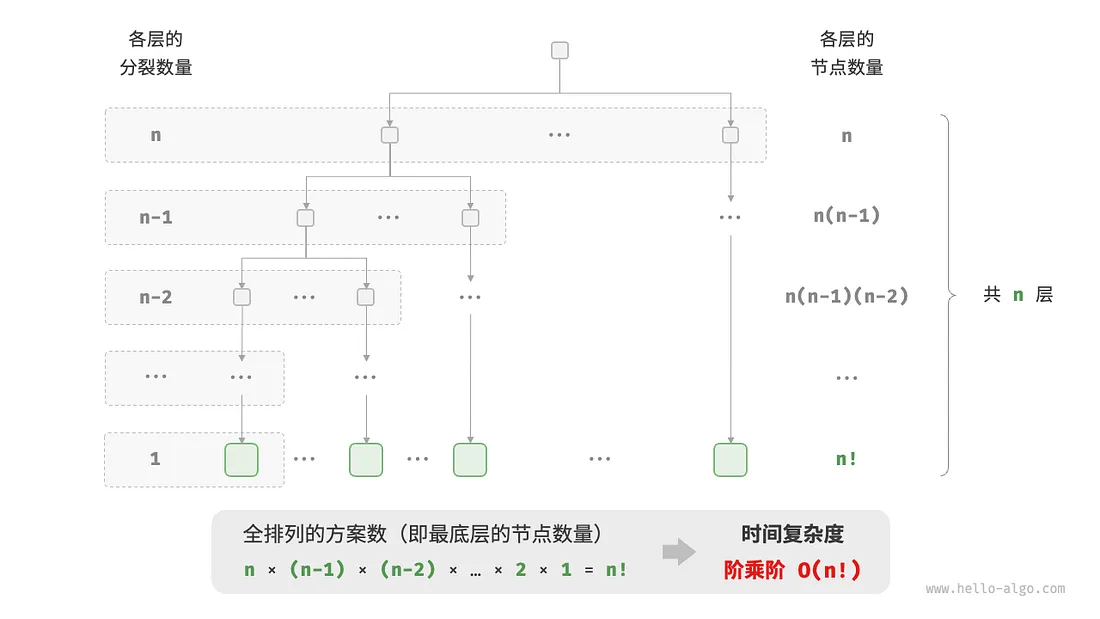
6. 阶乘阶 O(n!)

全排列问题

/* 阶乘阶（递归实现） */
int factorialRecur(int n) {
    if (n == 0)
        return 1;
    int count = 0;
    for (int i = 0; i < n; i++) {
        count += factorialRecur(n - 1);
    }
    return count;
}

2.3.5 最差、最佳、平均时间复杂度

最差时间复杂度更为实用，因为它给出了一个效率安全值。

通常使用最差时间复杂度作为算法效率的评判标准。

2.4 空间复杂度

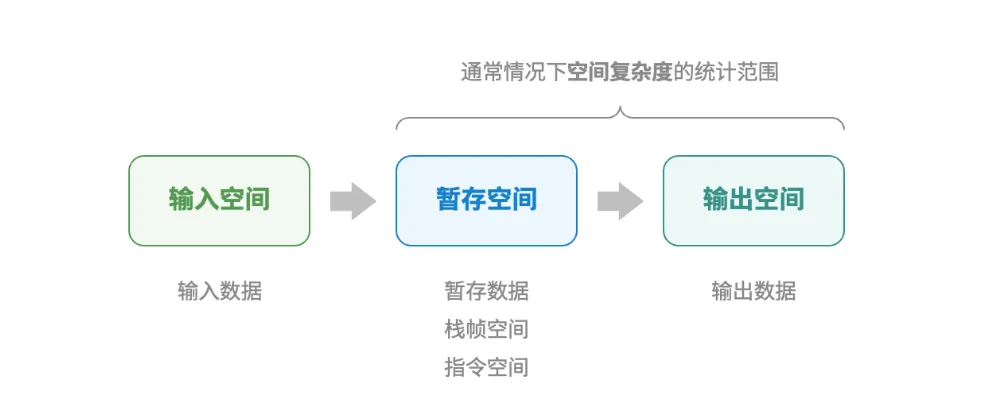
通常只关注最差空间复杂度，也就是最占用空间资源的情况下

递归函数中，需要注意统计栈帧空间：

int func() {
    // 执行某些操作
    return 0;
}
/* 循环的空间复杂度为 O(1) */
void loop(int n) {
    for (int i = 0; i < n; i++) {
        func();
    }
}
/* 递归的空间复杂度为 O(n) */
void recur(int n) {
    if (n == 1) return;
    return recur(n - 1);
}

常见类型：

1. 常数阶 O(1)

循环中初始化变量或调用函数而占用的内存，进入下次循环则被释放，不会累积占用空间。

/* 函数 */
int func() {
    // 执行某些操作
    return 0;
}

/* 常数阶 */
void constant(int n) {
    // 常量、变量、对象占用 O(1) 空间
    const int a = 0;
    int b = 0;
    int nums[1000];
    ListNode *node = newListNode(0);
    free(node);
    // 循环中的变量占用 O(1) 空间
    for (int i = 0; i < n; i++) {
        int c = 0;
    }
    // 循环中的函数占用 O(1) 空间
    for (int i = 0; i < n; i++) {
        func();
    }
}

2. 线性阶O(n)

常出现在元素数量与 n 成正比的数组、链表、栈、队列。

/* 哈希表 */
typedef struct {
    int key;
    int val;
    UT_hash_handle hh; // 基于 uthash.h 实现
} HashTable;

/* 线性阶 */
void linear(int n) {
    // 长度为 n 的数组占用 O(n) 空间
    int *nums = malloc(sizeof(int) * n);
    free(nums);

    // 长度为 n 的列表占用 O(n) 空间
    ListNode **nodes = malloc(sizeof(ListNode *) * n);
    for (int i = 0; i < n; i++) {
        nodes[i] = newListNode(i);
    }
    // 内存释放
    for (int i = 0; i < n; i++) {
        free(nodes[i]);
    }
    free(nodes);

    // 长度为 n 的哈希表占用 O(n) 空间
    HashTable *h = NULL;
    for (int i = 0; i < n; i++) {
        HashTable *tmp = malloc(sizeof(HashTable));
        tmp->key = i;
        tmp->val = i;
        HASH_ADD_INT(h, key, tmp);
    }

    // 内存释放
    HashTable *curr, *tmp;
    HASH_ITER(hh, h, curr, tmp) {
        HASH_DEL(h, curr);
        free(curr);
    }
}
//递归：线性阶
/* 线性阶（递归实现） */
void linearRecur(int n) {
    printf("递归 n = %d\r\n", n);
    if (n == 1)
        return;
    linearRecur(n - 1);
}

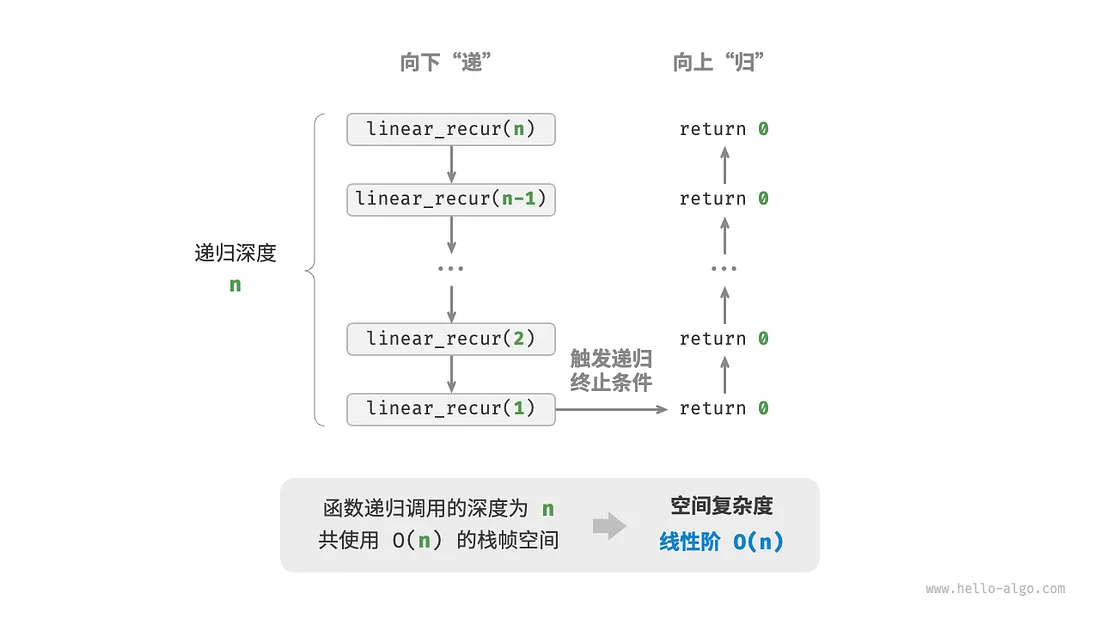
3. 平方阶O(n²)

常出现在矩阵、图。

void quadratic(int n) {
    // 二维列表占用 O(n^2) 空间
    int **numMatrix = malloc(sizeof(int *) * n);
    for (int i = 0; i < n; i++) {
        int *tmp = malloc(sizeof(int) * n);
        for (int j = 0; j < n; j++) {
            tmp[j] = 0;
        }
        numMatrix[i] = tmp;
    }

    // 内存释放
    for (int i = 0; i < n; i++) {
        free(numMatrix[i]);
    }
    free(numMatrix);
}
/* 平方阶（递归实现） */
int quadraticRecur(int n) {
    if (n <= 0)
        return 0;
    int *nums = malloc(sizeof(int) * n);
    printf("递归 n = %d 中的 nums 长度 = %d\r\n", n, n);
    int res = quadraticRecur(n - 1);
    free(nums);
    return res;
}

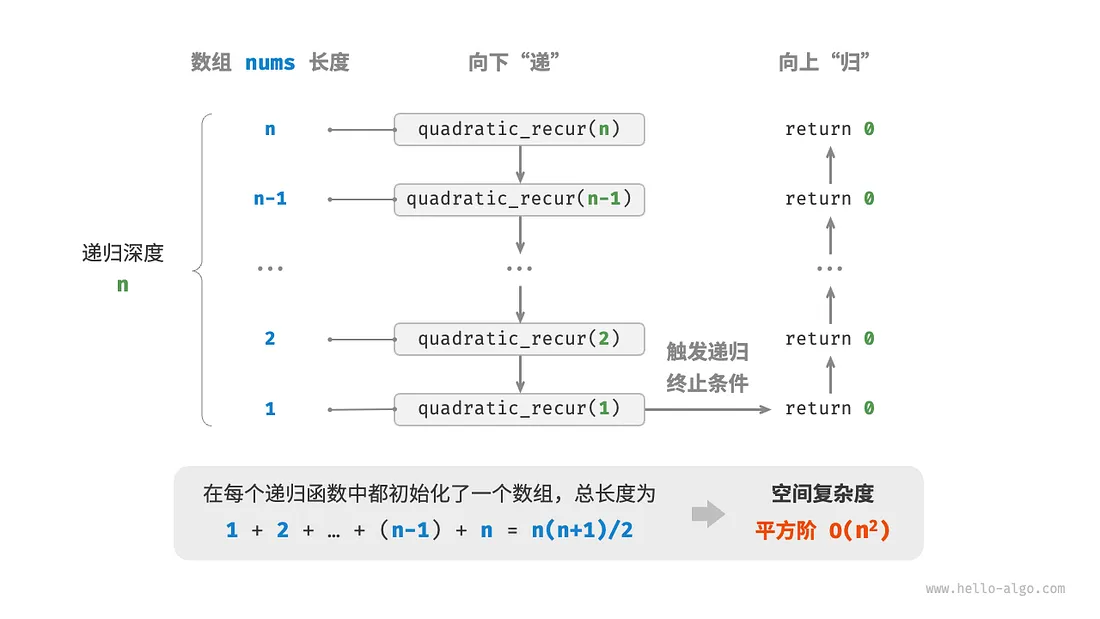
4. 指数阶 O(2^n)

常见于二叉树。

/* 指数阶（建立满二叉树） */
TreeNode *buildTree(int n) {
    if (n == 0)
        return NULL;
    TreeNode *root = newTreeNode(0);
    root->left = buildTree(n - 1);
    root->right = buildTree(n - 1);
    return root;
}

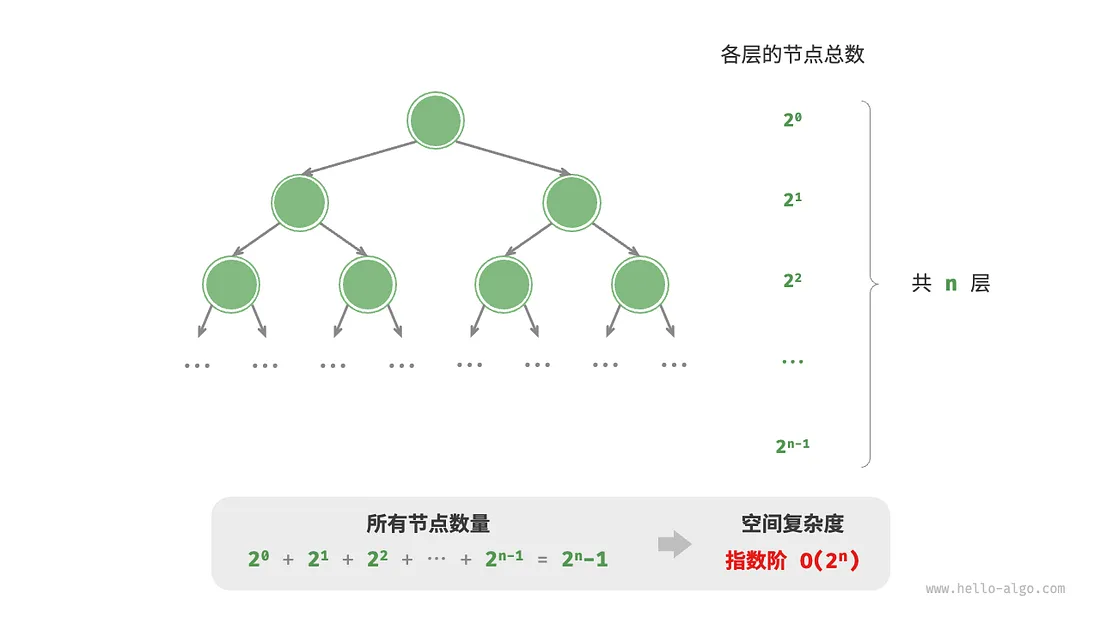
5. 对数阶 O(log n)

常见于分治算法。

3. 数据结构

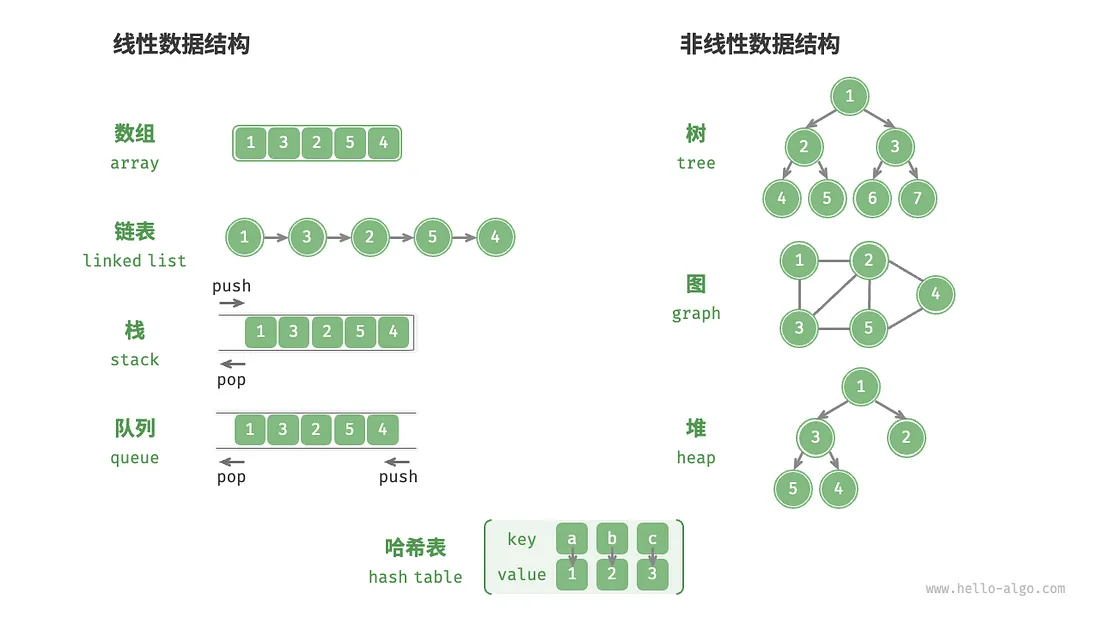
物理结构：连续空间存储（数组）、分散空间存储（链表）

所有数据结构都是基于数组、链表或二者的组合实现的。

动态数据结构：链表

静态数据结构：数组（初始化后长度不可变）

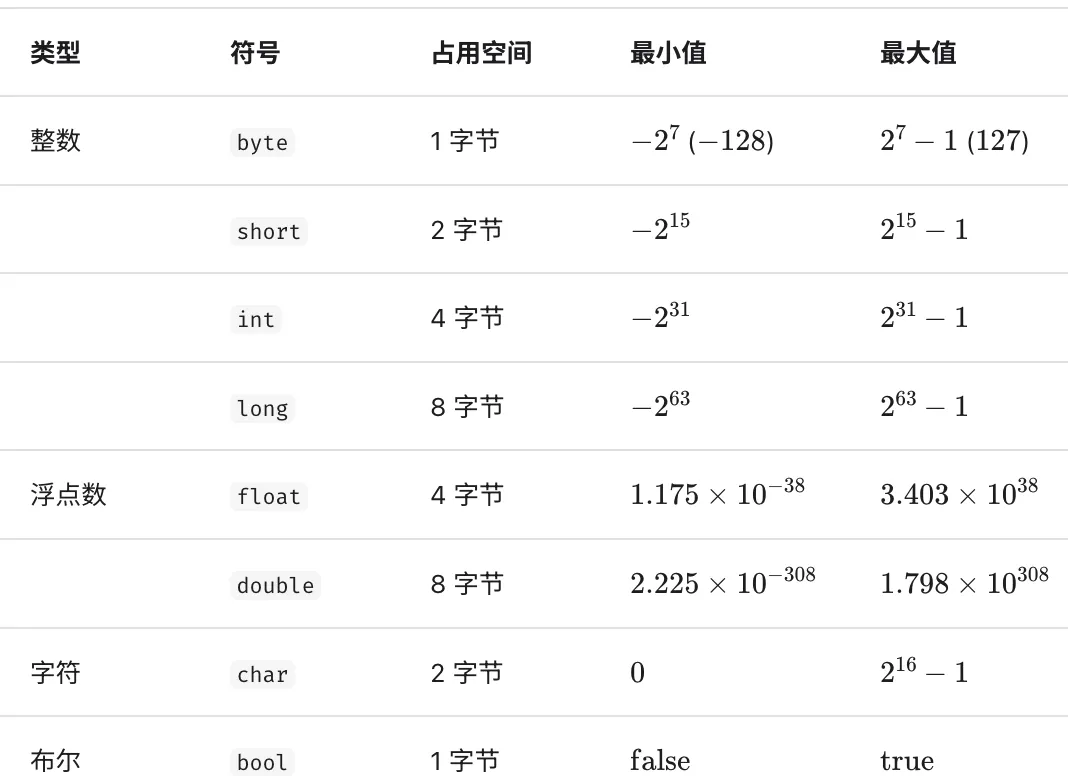
3.2 数据类型

//整型 字节 （位数=字节数*8） （最小值=-2^(位数-1) 最大值=2^(位数-1)-1）
byte 1 
short 2
int   4
long  8

//浮点数
float   4
double  8

//其他
bool   1
char   2
string

3.3 编码知识（常识）

原码 > 0 ，补码 = 原码 = 反码

原码 < 0 ，补码 = 反码 + 1 ，反码 = 原码除符号位外的所有位取反

（原码也可以是补码的反码+1）

特殊的补码： 1000_0000 代表 -128

3.3.2 浮点数编码

**float**` **的表示方式包含指数位，导致其取值范围远大于** `**int**

3.4 字符编码

// ASCII 码

// GBK 字符集：每个ASCII字符对应一个字节，每个汉字对应2个字节，因此char类型的字符可以是汉字

// Unicode字符集（统一码）

用这个Unicode字符集的话，当多种长度的 Unicode 码点同时出现在一个文本中时，系统如何解析字符？

其一解决方案：将所有字符存储为等长的编码（1字节的字符高位补0，扩充为2字节）

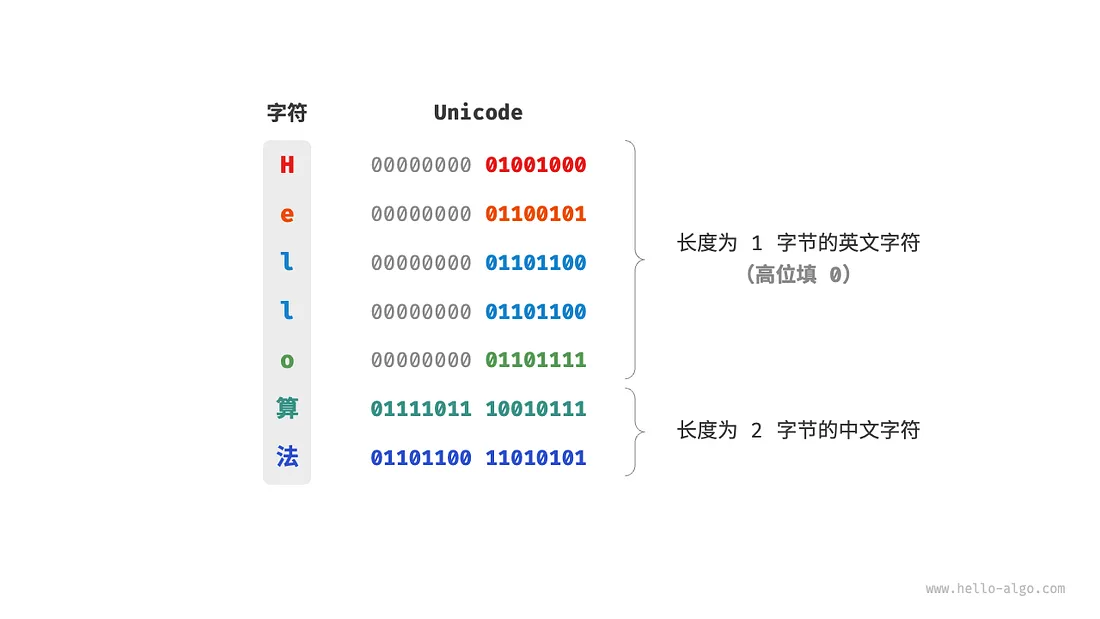
// UTF-8编码（最常用的Unicode字符集编码方式）

本质：可变长度编码

ASCII 字符只需 1 字节，拉丁字母和希腊字母需要 2 字节，常用的中文字符需要 3 字节，其他的一些生僻字符需要 4 字节。

UTF-16 编码：使用 2 或 4 字节来表示一个字符

UTF-32 编码：每个字符都使用 4 字节

// 编程语言的字符编码

采用 UTF-16 或 UTF-32 这类等长编码

posted @ 2025-03-06 20:21 EanoJiang 阅读(62) 评论(0) 收藏举报

刷新页面返回顶部

eanojiang

Hello 算法——只是开胃菜

1. 初识算法

2. (渐进)复杂度分析（asymptotic complexity analysis）

// for循环：适用于在预先知道迭代次数的情况下

// while循环

// 嵌套循环

//尾递归（tail recursion）

//递归树

// 栈

1. 常数阶 O(1)

2. 线性阶O(n)

3. 平方阶O(n²)

5. 对数阶O(log n)

6. 线性对数阶 O( nlog n )

6. 阶乘阶 O(n!)

1. 常数阶 O(1)

2. 线性阶O(n)

3. 平方阶O(n²)

4. 指数阶 O(2^n)

5. 对数阶 O(log n)

3. 数据结构

公告