20200723T3 小X的佛光
Description

Input

Output

Sample Input
3 3 1 1 2 2 3 1 2 3 1 1 3 3 1 3
Sample Output
1 1 3
Data Constraint
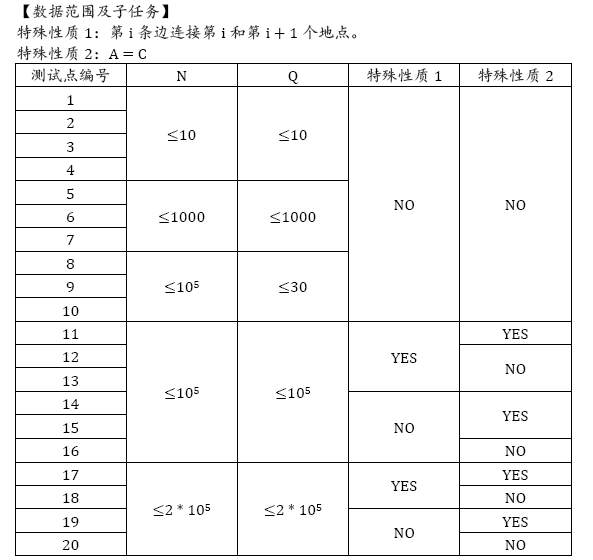
solution
题目意思就是求两条路径的交点数
LCA求即可
有两个点是一条200000的链
函数没开inline会爆栈
以后函数都加inline吧。。。
mlg别再折磨我的code了。。。
放一下官方题解

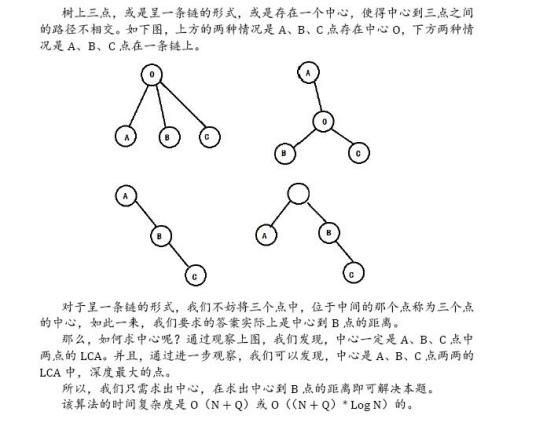
code
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<algorithm> 5 #include<cstring> 6 #include<queue> 7 #include<vector> 8 #include<stack> 9 #include<set> 10 #include<deque> 11 #include<map> 12 using namespace std; 13 14 template <typename T> void read(T &x) { 15 x = 0; int f = 1; char c; 16 for (c = getchar(); c < '0' || c > '9'; c = getchar()) if (c == '-') f = -f; 17 for (; c >= '0' && c <= '9'; c = getchar()) x = 10 * x + c - '0' ; 18 x *= f; 19 } 20 template <typename T> void write(T x){ 21 if (x < 0) putchar('-'), x = -x; 22 if (x > 9) write(x / 10); 23 putchar(x % 10 + '0'); 24 } 25 template <typename T> void writeln(T x) { write(x); putchar('\n'); } 26 template <typename T> void writesn(T x) { write(x); putchar(' '); } 27 28 #define int long long 29 #define inf 1234567890 30 #define next net 31 #define P 1000000007 32 #define N 400020 33 #define mid ((l+r)>>1) 34 #define lson (o<<1) 35 #define rson (o<<1|1) 36 #define R register 37 38 int n, q, num , A, B, C; 39 int cut, head[N ], next[N ], ver[N ]; 40 int deep[N ], f[N ][25]; 41 inline void add(int x,int y) 42 { 43 ver[++cut] = y; next[cut] = head[x]; head[x] = cut; 44 } 45 inline void dfs(int x,int fa) 46 { 47 deep[x] = deep[fa] + 1; 48 f[x][0] = fa; 49 for(R int i = head[x]; i; i = next[i]) 50 { 51 int y = ver[i]; 52 if(y == fa )continue; 53 dfs(y, x); 54 } 55 } 56 inline void work() 57 { 58 for(R int i = 1; i <= 20; i++) 59 for(R int j = 1; j <= n; j++) 60 f[j][i] = f[ f[j][i - 1] ][i - 1]; 61 } 62 inline int lca(int x,int y) 63 { 64 if(deep[x] < deep[y]) swap(x, y); 65 for(R int i = 20; i >= 0; i--) 66 if(deep[ f[x][i] ] >= deep[y]) x = f[x][i]; 67 if(x == y) return x; 68 for(R int i = 20; i >= 0; i--) 69 if(f[x][i] != f[y][i]) 70 { 71 x = f[x][i]; 72 y = f[y][i]; 73 } 74 return f[x][0]; 75 } 76 inline int calc(int x,int y) 77 { 78 return deep[x] + deep[y] - (deep[lca(x, y)] << 1) + 1; 79 } 80 signed main() 81 { 82 read(n); read(q); read(num ); 83 for(R int i = 1, x, y; i < n; i++) 84 { 85 read(x); read(y); 86 add(x,y); add(y,x); 87 } 88 dfs(1,0); 89 work(); 90 while(q--) 91 { 92 read(A); read(B); read(C); 93 writeln(calc(A, B) + calc(B, C) - calc(A, C) +1 >> 1); 94 } 95 return 0; 96 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号