排序算法
代码部分开发语言为python,编辑器为jupyter;
本文编码实现了冒泡排序,快速排序,选择排序,插入排序,归并排序,shell排序,堆排序;
利用jupyter代码块的计算耗时功能,记录了各种算法在30个数组元素下的排序耗时;
最后制作了一个表格,记录了在10,100,1000,10000等数组元素下各种算法的耗时,以便在工作中根据不同场景选择较优算法。
1 数据准备
1.1 代码实现
import random
def create_sort_array(array_length,repeat_length):
need_array = []
for i in range(array_length):
need_array.append(i)
for i in range(repeat_length): #加入相等数值干扰元素
need_array.append(i)
random.shuffle(need_array) #随机打乱顺序
return need_array
need_array = create_sort_array(25,5)
length = len(need_array)
print("初始数组为%s,长度为%d"%(need_array,length))

1.2 执行结果
初始数组为[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14],长度为30
2 冒泡排序
2.1 算法介绍
2.2 代码实现
#冒泡算法
def bubble_sort(sort_array):
for i,elem in enumerate(sort_array):
for j,elem in enumerate(sort_array[:length-i-1]):
if(sort_array[j]>sort_array[j+1]):
sort_array[j],sort_array[j+1] = sort_array[j+1],sort_array[j]
#print("第%d次排序后的数组:%s"%(i,sort_array))
return sort_array
bubble_array = need_array.copy()
bubble_sort(bubble_array)
print("冒泡排序前的数组为:%s\r\n冒泡排序后的数组为:%s"%(need_array,bubble_array))

2.3 执行结果
冒泡排序前的数组为:[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14] 冒泡排序后的数组为:[0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
3 快速排序
3.1 算法介绍
3.2 代码实现
#快速排序
def quick_sort(sort_array):
if(len(sort_array) < 2):
return
left = [x for x in sort_array[1:] if x < sort_array[0]]
right = [x for x in sort_array[1:] if x >= sort_array[0]]
quick_sort(left)
quick_sort(right)
sort_array[:] = left + [sort_array[0]] + right
quick_array = need_array.copy()
quick_sort(quick_array)
print("快速排序前的数组为:%s\r\n快速排序后的数组为:%s"%(need_array,quick_array))

3.3 执行结果
快速排序前的数组为:[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14] 快速排序后的数组为:[0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
4 选择排序
4.1 算法介绍
4.2 代码实现
#选择排序
def select_sort(sort_array):
for i,elem in enumerate(sort_array):
for j,elem in enumerate(sort_array[i:]):
if sort_array[i]>sort_array[i+j]:
sort_array[i],sort_array[i+j] = sort_array[i+j],sort_array[i]
#print("第%d次迭代交换后的数组为%s"%(i,sort_array))
#print("第%d次排序后的数组:%s"%(i,sort_array))
return sort_array
select_array = need_array.copy()
select_sort(select_array)
print("选择排序前的数组为:%s\r\n选择排序后的数组为:%s"%(need_array,select_array))

4.3 执行结果
选择排序前的数组为:[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14] 选择排序后的数组为:[0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
5 插入排序
5.1 算法介绍
5.2 代码实现
#插入排序
def insert_sort(sort_array):
for i,elem in enumerate(sort_array):
for j,elem in enumerate(sort_array[:i]):
if sort_array[j]>sort_array[i]:
sort_array.insert(j,sort_array[i])
del sort_array[i+1]
#print("第%d次排序后的数组:%s"%(i,sort_array))
return sort_array
insert_array = need_array.copy()
insert_sort(insert_array)
print("插入排序前的数组为:%s\r\n插入排序后的数组为:%s"%(need_array,insert_array))

5.3 执行结果
插入排序前的数组为:[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14] 插入排序后的数组为:[0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
6 归并排序
6.1 算法介绍
6.2 代码实现
#归并排序
def merge(sort_array, l, m, r):
n1,n2 = m - l + 1,r- m
L,R = [0] * (n1), [0] * (n2) # 创建临时数组
# 拷贝数据到临时数组 arrays L[] 和 R[]
for i in range(0 , n1):
L[i] = sort_array[l + i]
for j in range(0 , n2):
R[j] = sort_array[m + 1 + j]
# 归并临时数组到 arr[l..r]
i = 0 # 初始化第一个子数组的索引
j = 0 # 初始化第二个子数组的索引
k = l # 初始归并子数组的索引
while i < n1 and j < n2 :
if L[i] <= R[j]:
sort_array[k] = L[i]
i += 1
else:
sort_array[k] = R[j]
j += 1
k += 1
while i < n1: # 拷贝L[]的保留元素
sort_array[k] = L[i]
i += 1
k += 1
while j < n2: # 拷贝R[]的保留元素
sort_array[k] = R[j]
j += 1
k += 1
def merge_sort(sort_array,l,r):
if l < r:
m = int((l+(r-1))/2)
merge_sort(sort_array, l, m)
merge_sort(sort_array, m+1, r)
merge(sort_array, l, m, r)
def merge_sort_wrapper(sort_array):
merge_sort(sort_array,0,length-1)
merge_array = need_array.copy()
merge_sort_wrapper(merge_array)
print("归并排序前的数组为:%s\r\n归并排序后的数组为:%s"%(need_array,merge_array))


6.3 执行结果
归并排序前的数组为:[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14] 归并排序后的数组为:[0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
7 shell排序
7.1 算法介绍
7.2 代码实现
#shell排序
def shell_sort(sort_array):
dist= int(len(sort_array)/2)
while dist > 0:
for i in range(dist,len(sort_array)):
tmp=sort_array[i]
j = i
while j >= dist and tmp < sort_array[j - dist]:
sort_array[j] = sort_array[j - dist]
j -= dist
sort_array[j] = tmp
dist = int(dist/2)
shell_array = need_array.copy()
shell_sort(shell_array)
print("shell排序前的数组为:%s\r\nshell排序后的数组为:%s"%(need_array,shell_array))

7.3 执行结果
shell排序前的数组为:[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14] shell排序后的数组为:[0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
8 堆排序
8.1 算法介绍
8.2 代码实现
#堆排序
def heap_sort(sort_array):
n = len(sort_array)
for i in range(n, -1, -1): # Build a maxheap.
heapify(sort_array, n, i)
for i in range(n-1, 0, -1): # 一个个交换元素
sort_array[i], sort_array[0] = sort_array[0], sort_array[i]
heapify(sort_array, i, 0)
def heapify(sort_array, n, i):
largest = i
l = 2 * i + 1 # left = 2*i + 1
r = 2 * i + 2 # right = 2*i + 2
if l < n and sort_array[i] < sort_array[l]:
largest = l
if r < n and sort_array[largest] < sort_array[r]:
largest = r
if largest != i:
sort_array[i],sort_array[largest] = sort_array[largest],sort_array[i]
heapify(sort_array, n, largest)
heap_array = need_array.copy()
heap_sort(heap_array)
print("堆排序前的数组为:%s\r\n堆排序后的数组为:%s"%(need_array,heap_array))

8.3 执行结果
堆排序前的数组为:[1, 1, 23, 12, 22, 6, 13, 19, 2, 5, 3, 18, 9, 24, 4, 7, 0, 17, 11, 4, 2, 16, 0, 20, 10, 3, 8, 15, 21, 14] 堆排序后的数组为:[0, 0, 1, 1, 2, 2, 3, 3, 4, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24]
9 各种场景下排序算法对比
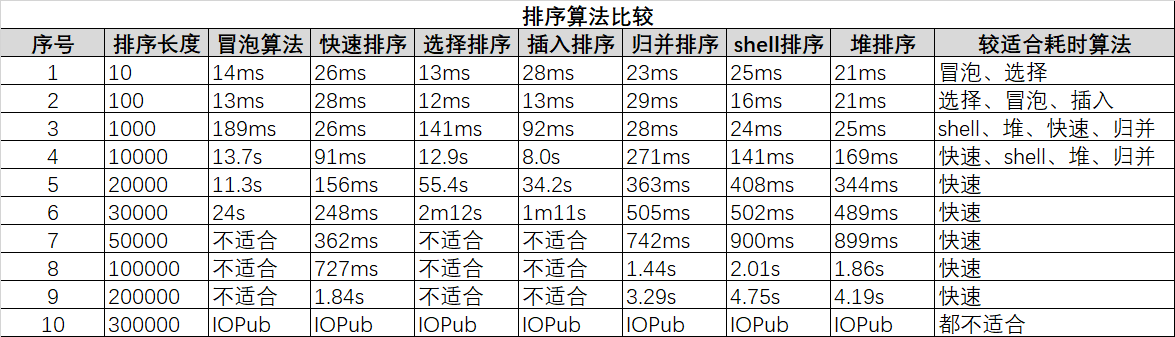
由表格数据可知:快速排序在各种场景下均比较稳定,需重点关注。
说明:
不适合为该场景下算法已证明被淘汰
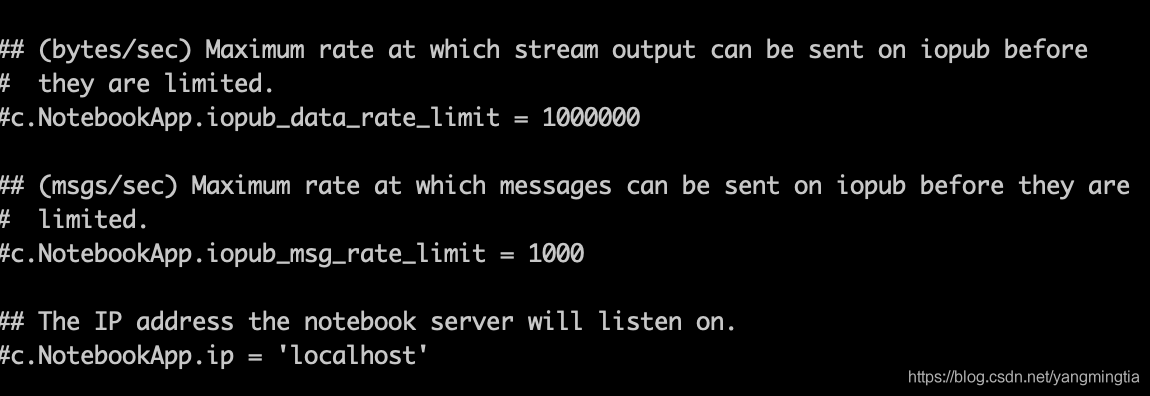
IOPub为IOPub data rate exceeded。data_rate_limit 默认1000000个,可以通过修改jupyter的配置解决,但不在本文讨论范围,不做具体介绍。
IOPub data rate exceeded. 已超过IOPub数据速率。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号