FFT快速傅里叶变换

FFT

我们从一个问题进行讨论\(FFT\)，我们有两个多项式\(A(x)=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1},\\ B(x)=b_0+b_1x+b_2x^2+\dots+b_{m-1}x^{m-1}\)我们现在要求\(A(x)\cdot B(x)\)。朴素算法是显而易见的，时间复杂度是\(\Theta(nm)\)暴力相乘即可，但这个时间复杂度我们是接受不了的。这时我们可以引入一个点值表示法。

前置知识

点值表示法

多项式通常有两种表示方法，一种是系数表示法即形如\(P(x)=\sum_{i=0}^{n-1}a_ix^i\)的表示法，而点值表示法则是把\(n\)个互不相同的数\(x\)带入多项式\(P(x)\)中的的值作为\(y\)值确定\(n\)个点，我们可以证明互不重合的\(n\)个点可以唯一确定一个多项式。

单位根

对于\(\omega^n=1\)的解傅里叶得出的结论是，对于\(\omega^n=1\)这个方程的复数解为，在复平面上我们对单位圆从正实数轴开始\(n\)等分如图，这\(n\)个\(n\)等分点表示的复数即为原方程的复数解。

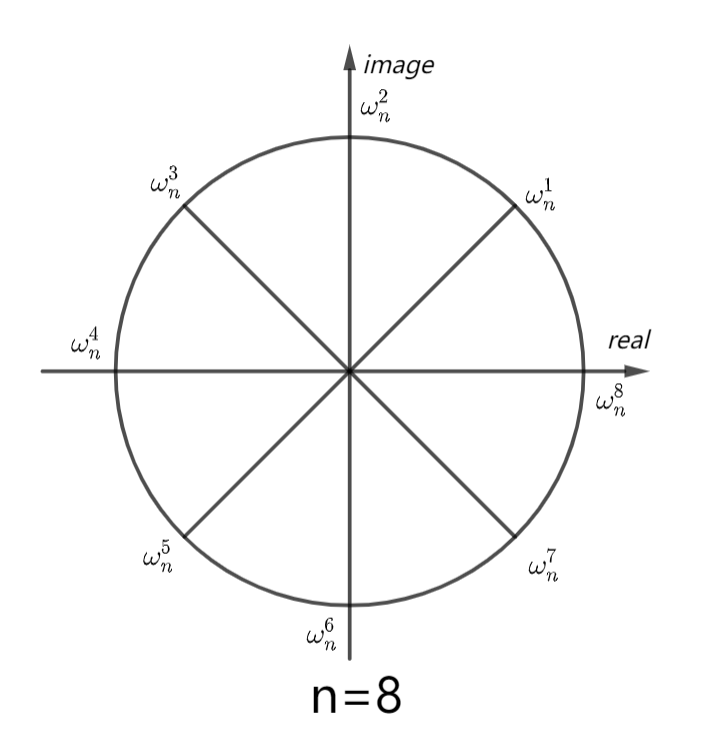
我们可以得到以下性质

• \(\omega_n^k=\cos\frac{2k\pi}{n}+i\sin\frac{2k\pi}{n}\)
• \(\forall i\neq j\)，\(i,j<n\)，有\(\omega_n^i\neq\omega_n^j\)
• \(\omega_{2n}^{2k}=\omega_n^k\)（折半引理）
• \(\omega_n^k=-\omega_n^{k+\frac n2}\)
• \(\omega_n^0=\omega_n^n\)
• \(\omega_n^i\cdot\omega_n^j=\omega_n^{i+j}\)

FFT推导

正变换

我们要把一个多项式转为点值表示法，朴素转是\(\Theta(n^2)\)，达不到我们的目的。这里我们要把\(n\)转为一个\(2\)的幂的数不够就补位系数补\(0\)，这样我们可以把多项式分为两个部分

\[\begin{align}A(x)&=a_0+a_1x+a_2x^2+\dots+a_{n-1}x^{n-1}\\&=(a_0+a_2x^2+\cdots+a_{n-2}x^{n-2})+(a_1+a_3x^3+\dots+a_{n-1}x^{n-1})\end{align} \]

令\(A_1(x)=a_0+a_2x+\cdots+a_{n-2}x^{\frac n2-1}\)，\(A_2(x)=a_1+a_3x^2+\dots+a_{n-1}x^{\frac n2-1}\)

可得\(A(x)=A_1(x^2)+xA_2(x^2)\)

我们可以带入\(n\)个\(n\)次单位根

\[k\in\bigg[0,\frac n2-1\bigg],A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})=A_1(\omega_{\frac n2}^{k})+\omega_n^kA_2(\omega_{\frac n2}^{k})\\ k\in\bigg[\frac n2-1,n-1\bigg],A(\omega_n^{k+\frac n2})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac n2}A_2(\omega_n^{2k+n})=A_1(\omega_{\frac n2}^{k})-\omega_n^kA_2(\omega_{\frac n2}^{k}) \]

这样我们可以通过分治\(\log_2n\)层，这样我们可以在\(n\log_2n\)的时间里求出\(n\)个单位根的多项式值，我们把两个多项式的每个单位根对应的多项式值算出来，把同一单位根的两个多项式的值相乘，便可以得到乘积多项式的点值表达式。但在一些数据优秀的\(OJ\)上我们并不能通过，所以我们需要一个蝴蝶变换来优化。

蝴蝶变换

我们会发现一个规律，一个项的最后拆分位置恰好为下标的二进制反过来，我们以\(8\)项的多项式为例，模拟拆分的过程：

位置编号（二进制）	\(000\)	\(001\)	\(010\)	\(011\)	\(100\)	\(101\)	\(110\)	\(111\)
初始序列	\(x_0\)	\(x_1\)	\(x_2\)	\(x_3\)	\(x_4\)	\(x_5\)	\(x_6\)	\(x_7\)
一次拆分后	\(x_0\)	\(x_2\)	\(x_4\)	\(x_6\)	\(x_1\)	\(x_3\)	\(x_5\)	\(x_7\)
两次拆分后	\(x_0\)	\(x_4\)	\(x_2\)	\(x_6\)	\(x_1\)	\(x_5\)	\(x_3\)	\(x_7\)
三次拆分后	\(x_{0(000)}\)	\(x_{4(100)}\)	\(x_{2(010)}\)	\(x_{6(110)}\)	\(x_{1(001)}\)	\(x_{5(101)}\)	\(x_{3(011)}\)	\(x_{7(111)}\)

我们就可以得到一个迭代版的\(FFT\)这样是可以通过所有\(OJ\)的洗礼的。

逆变换

正变换我们其实是求了这样一个东西

\[\begin{bmatrix} 1&1&1&\cdots&1\\ 1&\omega_n^1&\omega_n^2&\cdots&\omega^{n-1}\\ 1&\omega_n^2&\omega_n^4&\cdots&\omega^{2n-2}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 1&\omega_{n-1}^{n-1}&\omega_{n-1}^{2n-2}&\cdots&\omega_{n-1}^{(n-1)^2} \end{bmatrix} \begin{bmatrix} a_0\\a_1\\a_2\\\vdots\\a_{n-1} \end{bmatrix}= \begin{bmatrix} A_0\\A_1\\A_2\\\vdots\\a_{n-1} \end{bmatrix} \]

由于这个矩阵的元素非常特殊，它的逆矩阵也有特殊的性质，就是每一项取倒数再除以变换的长度就能得到它的逆矩阵。

我们可以得到

\[\frac{1}{\omega_k}=\omega_k^{-1}=e^{-\frac{2\pi i}{k}}=\cos(\frac{2\pi}{k})+i\sin(-\frac{2\pi}k)=\cos(\frac{2\pi}k)-i\sin(\frac{2\pi}k) \]

只需要我们在正变换的函数里面多传一个系数，表示正/逆变换，在计算的时候乘上系数即可。

code

const double Pi=acos(-1);
struct _cp{
    double re,im;
    inline _cp operator + (const _cp b)const
    {return (_cp){re+b.re,im+b.im};}
    inline _cp operator - (const _cp b)const
    {return (_cp){re-b.re,im-b.im};}
    inline _cp operator * (const _cp b)const
    {return (_cp){re*b.re-im*b.im,re*b.im+im*b.re};}
    inline _cp operator / (const _cp b)const{
        _cp x=(_cp){re,im};double q=b.re*b.re+b.im*b.im;
        _cp y=(_cp){b.re/q,b.im/q};
        return x*y;
    }
};//自己写的复数运算
int rev[5000005];
void FFT(_cp *a,int n,int inv)//inv为逆变换系数
{
    int bit=0;
    while((1<<bit)<n)bit++;
    for(int i=0;i<n;i++){
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
        if(i<rev[i])swap(a[i],a[rev[i]]);
    }
    for(int mid=1;mid<n;mid*=2){
    	_cp temp=(_cp){cos(Pi/mid),inv*sin(Pi/mid)};
        for(int i=0;i<n;i+=mid*2){
            _cp omega=(_cp){1,0};
            for(int j=0;j<mid;j++,omega=omega*temp){
                _cp x=a[i+j],y=omega*a[i+j+mid];
                a[i+j]=x+y,a[i+j+mid]=x-y;
            }
        }
    }
}