[NOI2002]荒岛野人（exgcd）

现在看来一道很水的\(exgcd\)在当年竟是一道\(NOI\)题目。

原题面

题目描述

克里特岛以野人群居而著称。岛上有排列成环行的\(m\)个山洞。这些山洞顺时针编号为\(1,2,\cdots,m\)。岛上住着\(n\) 个野人，一开始依次住在山洞\(C_1,C_2,\cdots,C_n\)中，以后每年，第\(i\)个野人会沿顺时针向前走\(P_i\)个洞住下来。

每个野人\(i\)有一个寿命值\(L_i\)，即生存的年数。

下面四幅图描述了一个有\(6\)个山洞，住有三个野人的岛上前四年的情况。三个野人初始的洞穴编号依次为\(1,2,3;\)每年要走过的洞穴数依次为 \(3,7,2;\)寿命值依次为\(4,3,1\)。

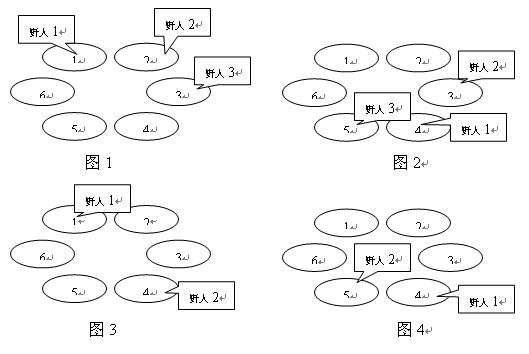奇怪的是，虽然野人有很多，但没有任何两个野人在有生之年处在同一个山洞中，使得小岛一直保持和平与宁静，这让科学家们很是惊奇。他们想知道，至少有多少个山洞，才能维持岛上的和平呢？

输入格式

第\(n\)行为一个整数\(n(1\leq n\leq 15)\)，即野人的数目。

第\(2\)行到第\(N+1\)每行为三个整数\(C_i, P_i, L_i (1\leq C_i,P_i \leq 100, 0\leq L_i\leq 10^6 )\)，表示每个野人所住的初始洞穴编号，每年走过的洞穴数及寿命值。

输出格式

仅包含一个数\(M\)，即最少可能的山洞数。输入数据保证有解，且 \(M\)不大于\(10^6\)。

样例输入

3
1 3 4
2 7 3
3 2 1

样例输出

6

说明/提示

\(1\le N\le15\)，\(1\leq C_i,P_i\leq 100\)，\(0\leq L_i\leq 10^6\)

保证\(M\le10^6\)

题解

我们从小到大枚举答案，我们再枚举两个不同的野人\(i,j\)，我们判断\(i,j\)在寿命值范围内能否相遇，能就说明枚举的答案不合法，如果所有\(i,j\)都不能相遇，那就说明合法，输出答案结束程序。

如何判断

我们现在的问题是如何判断他们能否相遇。

\(\forall i,j\)设\(a=P_i-P_j\)即一年\(i\)比\(j\)多走的步数，\(x\)天后相遇，\(b=C_j-C_i\)即\(j\)初始的位置在\(i\)前面多少单位。我们的判断变为判断\(ax\equiv b(\mod M)\)，我们转化一下可得\(ax+My=b\)的整数解。

这样就可以用扩展欧几里德来解决了，时间复杂度是\(O(MN^2\log M)\)可以通过本体。

code

#include<bits/stdc++.h>
#define fre(x) freopen(#x".in","r",stdin),freopen(#x".out","w",stdout);
using namespace std;
int n,c[25],p[25],l[25],w;
int max(int a,int b){return (a>b)?a:b;}
int exgcd(int a,int b,int &x,int &y)
{
    if(b==0)
    {
        x=1;y=0;
        return a;
    }
    int d=exgcd(b,a%b,y,x);
    y=y-a/b*x;
    return d;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d%d",&c[i],&p[i],&l[i]);
        w=max(w,c[i]);
    }
    for(int d,x,y,a,b;;w++)
    {
        bool flag=0;
        for(int i=1;i<n;i++)
        {
            for(int j=i+1;j<=n;j++)
            {
                a=p[i]-p[j];b=c[j]-c[i];
                if(a<0)a=-a,b=-b;
                d=exgcd(a,w,x,y);
                int m=w/d;
                x=(x*b/d%m+m)%m;
                if(!x)x+=m;
                if(b%d==0&&x<=l[i]&&x<=l[j])flag=1;
                if(flag)break;
            }
            if(flag)break;
        }
        if(!flag){printf("%d",w);return 0;}
    }
    return 0;
}