微积分笔记（一）

求导的定义

求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与自变量的增量之商的极限。在一个函数存在导数时，称这个函数可导 或者可微分。可导的函数一定连续。不连续的函数一定不可导。

定义法求导

定义式

\[f'(x)=\frac{dy}{dx}=\lim_{h\to0}\frac{f(x+h)-f(x)}{h} \]

例一

题目

求\(f(x)=\sqrt x\)的导数

解答

\[\begin{align} f'(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\sqrt{x+h}-\sqrt x}{h}\\ &=\lim_{h\to0}\frac{(\sqrt{x+h}-\sqrt x)(\sqrt{x+h}+\sqrt x)}{h(\sqrt{x+h}+\sqrt x)}\\ &=\lim_{h\to0}\frac{x+h-h}{h(\sqrt{x+h}+\sqrt x)}\\ &=\lim_{h\to0}\frac1{\sqrt{x+h}+\sqrt x}\\ &=\frac 1{2\sqrt x} \end{align} \]

例二

题目

求\(f(x)=\frac1x\)的导数

解答

\[\begin{align} f'(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\frac1{x+h}-\frac1x}{h}\\ &=\lim_{h\to0}\frac{-\frac{h}{x(x+h)}}{h}\\ &=-\lim_{h\to0}\frac1{x(x+h)}\\ &=-\frac1{x^2} \end{align} \]

多项式求导公式

若\(f(x)=x^a\)则\(f'(x)=ax^{a-1}\)

求导运算公式求导

和法则

\[[f(x)+g(x)]'=f(x)'+g(x)'\\ \frac{dy}{dx}=\frac{d(u+v)}{dx}=\frac{du}{dx}+\frac{dv}{dx} \]

积法则

\[[f(x)g(x)]'=f(x)g'(x)+f'(x)g(x)\\ \frac{dy}{dx}=\frac{d(uv)}{dx}=u\frac{dv}{dx}+v\frac{du}{dx} \]

商法则

\[\Big[\frac{f(x)}{g(x)}\Big]'=\frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\\ \frac{dy}{dx}=\frac{d(\frac uv)}{dx}=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2} \]

例一

题目

求\(f(x)=\frac{(x+1)^2}{x^2+1}\)的导数

解答

\[f(x)=\frac{x^2+2x+1}{x^2+1}=1+\frac{2x}{x^2+1} \]

令\(u=2x,v=x^2+1\)

则\(\frac{du}{dx}=2,\frac{dv}{dx}=2x\)

用导数运算的商法则

\[\begin{align} f'(x)=\frac{dy}{dx}&=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}\\ &=\frac{2x(x^2+1)-2x\cdot2x}{(x^2+1)^2}\\ &=\frac{2x^3-4x^2+2x}{x^4+2x^2+1}\\ \end{align} \]

三角函数的导数（一）

两个重要的极限

\[\lim_{h\to0}\frac {\sin x} x=1\qquad\lim_{h\to0}\frac{\cos x-1}{x}=0 \]

基础三角函数的导数

正弦函数的导数

\[\begin{align} \sin'(x)=\frac{dy}{dx}&= \lim_{h\to0}\frac{\sin(x+h)-\sin(x)}{h}\\ &=\lim_{h\to0}\frac{\sin(x)\cos(h)+\cos(x)\sin(h)-\sin(x)}{h}\\ &=\lim_{h\to0}\frac{\sin(x)[\cos(h)-1]+\cos(x)\sin(h)}{h}\\ &=\lim_{h\to0}\sin(x)\cdot\frac{\cos(h)-1}{h}+\cos(x)\frac{\sin(h)}{h}\\ &=\cos(x) \end{align} \]

余弦函数的导数

\[\begin{align}\cos'(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\cos(x+h)-\cos(x)}{h}\\&=\lim_{h\to0}\frac{\cos(x)\cos(h)-\sin(x)\sin(h)-\cos(x)}{h}\\&=\lim_{h\to0}\frac{\cos(x)[\cos(h)-1]-\sin(x)\sin(h)}{h}\\ &=\lim_{h\to0}\cos(x)\cdot\frac{\cos(h)-1}{h}-\sin(x)\frac{\sin(h)}{h}\\&=-\sin(x)\end{align} \]

正切函数的导数

令\(u=\sin(x),v=\cos(x)\)，则\(\frac{du}{dx}=\cos(x),\frac{dv}{dx}=-\sin(x)\)

\[\begin{align} \tan'(x)=\Big(\frac{u}{v}\Big)'&=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}\\ &=\frac{\cos^2(x)+\sin^2(x)}{\cos^2(x)}\\ &=\frac1{\cos^2(x)}\\ &=\sec^2(x) \end{align} \]

余切函数的导数

令\(u=\cos(x),v=\sin(x)\)，则\(\frac{du}{dx}=-\sin(x)，\frac{dv}{dx}=\cos(x),\)

\[\begin{align} \cot'(x)=\Big(\frac{u}{v}\Big)'&=\frac{v\frac{du}{dx}-u\frac{dv}{dx}}{v^2}\\ &=\frac{-\sin^2(x)-\cos^2(x)}{\sin^2(x)}\\ &=-\frac1{\sin^2(x)}\\ &=-\csc^2(x) \end{align} \]

正割函数的导数

令\(u=\cos x\)，则\(\frac{du}{dx}=-\sin(x),\frac{dy}{du}=-\frac{1}{u^2}\)

\[\sec'(x)=\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}=\frac{\sin(x)}{\cos^2(x)}=\tan(x)\sec(x) \]

余割函数的导数

令\(u=\sin x\)，则\(\frac{du}{dx}=\cos(x),\frac{dy}{du}=-\frac{1}{u^2}\)

\[\csc'(x)=\frac{dy}{dx}=\frac{dy}{du}\cdot\frac{du}{dx}=-\frac{\cos(x)}{\sin^2(x)}=\cot(x)\csc(x) \]

例一

题目

求\(f(x)=x\sin(5x)\)的导数

解答

令\(U=x,V=\sin(5x)\)

令\(u=5x\)则\(\frac{du}{dx}=5,\frac{dV}{du}=-\cos(u)\)

\[\frac{dV}{dx}=\frac{dV}{du}\cdot\frac{du}{dx}=-5\cos(5x) \]

因为\(\frac{dU}{dx}=1,\frac{dV}{dx}=-5\cos(5x)\)

\[f'(x)=U\frac{dV}{dx}+V\frac{dU}{dx}=-5x\cos(5x)+\sin(5x) \]

指数函数与对数函数的导数

\(e\)的定义

假设你在一家银行里存钱，若一笔存在银行里的时间为一年的\(\frac 1n\)，你将获得本金\(\frac 1n\)的利息，很明显你一钱存越多次能获得的利息越多（假设你每次存钱），但这是无上限的吗？很显然是不可能的。

我们可以列表

\(n\)	\(1\)	\(2\)	\(3\)	\(4\)	\(\cdots\)	\(100\)	\(\cdots\)	\(10^4\)
连本利率	\(2\)	\(2.25\)	\(2.37\)	\(2.4414\)	\(\cdots\)	\(2.704813\)	\(\cdots\)	\(2.7181459\)

当你的\(n\)足够大时，连本利率的增长速度变得极为缓慢（从\(100\)增长到\(10^4\)，连本利率只增加了\(0.013\)左右），它应该收敛与某个常数。

这样我们引出了自然常数\(e\)，它定义为\(e=\lim_{n\to\infin}(1+\frac1n)^n\)，它约等于\(2.718281\)，我们待会会说明为什么被称为自然常数。

指数函数的导数

我们先求\(f(x)=a^x\)的导数

用导数的定义式来求

\[\begin{align} f'(x)=\frac{dy}{dx}&=\lim_{h\to 0}\frac{a^{x+h}-a^x}{h}\\ &=\lim_{h\to 0}\frac{a^x(a^h-1)}{h}\\ &=a^x\lim_{h\to0}\frac{a^h-1}{h}\\ \end{align} \]

令\(t=a^h-1\)则\(h=\log_a{t+1}\),当\(\lim_{h\to0}t=0\)得

\[\begin{align} f'(x)&=a^x\lim_{t\to0}\frac{t}{\log_at+1}\\ &=a^x\lim_{t\to0}\frac{1}{\log_a(1+t)^{\frac1t}}\\ &=a^x\frac{1}{\log_ae}\\ &=a^x\frac{\ln a}{\ln e}\\ &=a^x\ln a \end{align} \]

对数函数的导数

我们讨论\(f(x)=\log_ax\)的导数

用导数的定义式来求

\[\begin{align} f'(x)=\frac{dy}{dx}&=\lim_{h\to0}\frac{\log_a(x+h)-\log_ax}{h}\\ &=\lim_{h\to0}\frac{\log_a(1+\frac h x)}{h}\\ &=\lim_{h\to 0}\log_a(1+\frac hx)^{\frac{1}{h}}\\ &=\lim_{h\to 0}\frac 1x\log_a(1+\frac hx)^{\frac xh}\\ \end{align} \]

令\(t=\frac xh\)，当\(\lim_{h\to0}t=\infin\)得

\[\begin{align} f'(x)&=\lim_{t\to\infin}\frac1x\log(1+\frac1t)^t\\ &=\frac1x\log_ae\\ &=\frac1x\cdot\frac{\ln e}{\ln a}=\frac{1}{x\ln a} \end{align} \]

隐函数求导

隐函数的定义

如果方程\(f(x,y)=0\)能确定\(y\)是\(x\)的函数，那么称这种方式表示的函数是隐函数。而函数就是指：在某一变化过程中，两个变量\(x\)、\(y\)，对于某一范围内的\(x\)的每一个值，\(y\)都有确定的值和它对应，\(y\)就是\(x\)的函数。这种关系一般用\(y=f(x)\)即显函数来表示。\(f(x,y)=0\)即隐函数是相对于显函数来说的。

隐函数的求导方法

我们可以举出一个相当经典的隐函数\(x^2+y^2=1\)

我们尝试求出它在点\((x,y)\)点的切线斜率\(\frac{dy}{dx}\)

首先我们把\(x\)和\(y\)放在等号两边得\(x^2-1=-y^2\)

我们对两边同时求导左边是相当方便的，可得\((x^2-1)'=2x\)

但我们对右边求导时出现了问题我们要求的是\(\frac{dy}{dx}\)但我们的变化量为\(dy\)

我们可使用链式求导法则\(\frac{d(-y^2)}{dy}\frac{dy}{dx}=-2y\frac{dy}{dx}\)

整理后为\(2x=-2y\frac{dy}{dx}\)即\(\frac{dy}{dx}=-\frac xy\)。

通过两边同时对\(x\)求导我们便解决了隐函数的求导问题

例一

题目

\(f:e^xy^3-x^2+2y=1\)，求\(\frac{dy}{dx}\),\(\frac {d^2y}{dx^2}\)

解答

求\(\frac{dy}{dx}\)，我们先对\(x\)求导，得\(e^xy^3+e^x3y^2\frac{dy}{dx}-2x+2\frac{dy}{dx}=0\)

可得\(\frac{dy}{dx}=\frac{2x-e^xy^3}{3e^xy^2+2}\)

求\(\frac{d^2y}{dx^2}\)，对\(e^xy^3+e^x3y^2\frac{dy}{dx}-2x+2\frac{dy}{dx}=0\)再次对\(x\)求导

得\(e^xy^3+3e^xy^2\frac{dy}{dx}+3e^xy^2\frac{dy}{dx}+6e^xy(\frac{dy}{dx})^2+3e^xy^2\frac{d^2y}{dx^2}-2+2\frac{d^2y}{dx^2}=0\)

则\(\frac{d^2y}{dx^2}=\frac{2-e^xy^3-6e^xy^2\frac{dy}{dx}+6e^xy(\frac{dy}{dx}^2)}{3e^xy^2+2}\)，其中\(\frac{dy}{dx}=\frac{2x-e^xy^3}{3e^xy^2+2}\)

三角函数求导（二）

反三角函数的导数

反正弦函数的导数

因为\(y=\arcsin(x)\)，所以\(x=\sin(y)\)

我们对\(x=\sin(y)\)关于\(x\)进行隐函数求导，得\(1=\cos(y)\frac{dy}{dx}\)

因为\(x=\sin(y)\)，所以\(\cos(y)=\pm\sqrt{1-x^2}\)。

所以\(\frac{dy}{dx}=\pm\frac{1}{\sqrt{1-x^2}}\)中的一个。我们可以分析\(y=\arcsin(x)\)的图像

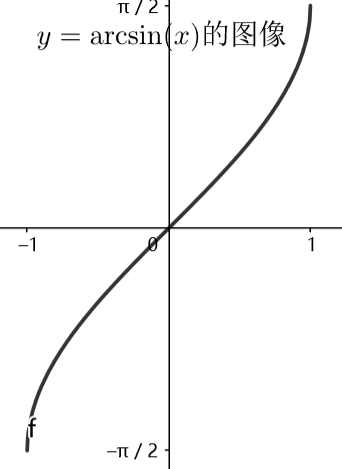
容易发现\(y=\arcsin(x)\)是导数恒为正的增函数，所以\(\frac{dy}{dx}=\frac{1}{\sqrt{1-x^2}}\)

反余弦函数的导数

因为\(y=\arccos(x)\)，所以\(x=\cos(y)\)

我们对\(x=\cos(y)\)关于\(x\)进行隐函数求导，得\(1=-\sin(y)\frac{dy}{dx}\)

因为\(x=\cos(y)\)，所以\(\sin(y)=\pm\sqrt{1-x^2}\)。

所以\(\frac{dy}{dx}=\pm\frac{1}{\sqrt{1-x^2}}\)中的一个。我们可以分析\(y=\arccos(x)\)的图像

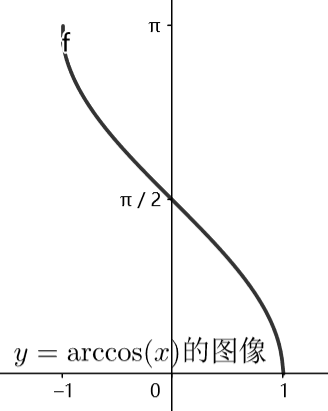
容易发现\(y=\arccos(x)\)是导数恒为负的减函数，所以\(\frac{dy}{dx}=-\frac{1}{\sqrt{1-x^2}}\)

反正切/余切函数的导数

因为\(y=\arctan(x)\)，所以\(x=\tan(y)\)

我们对\(x=\tan(y)\)关于\(x\)隐函数求导得\(\frac{dy}{dx}=\frac{1}{\sec^2(y)}=\frac{1}{x^2+1}\)

同理\(y=\cot^{-1}(x)\)，所以\(x=\cot(y)\)

我们对\(x=\cot(y)\)关于\(x\)隐函数求导，得\(\frac{dy}{dx}=-\frac{1}{\csc^2(y)}=-\frac{1}{1+x^2}\)

反正割/余割函数的导数

我们与上面做法相同，由\(y=\sec^{-1}(x)\)，所以\(x=\sec(y)\)

我们对\(x=\sec(y)\)对于\(x\)隐函数求导得\(\frac{dy}{dx}=\frac{1}{\sec(y)\tan(y)}=\frac{1}{\pm x\sqrt{x^2-1}}\)

又出现了考虑正负的情况，我们可以分析图像

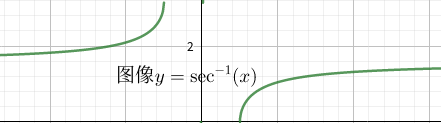
发现它是恒正的，可得\(\sec^{-1}(x)'=\frac{1}{|x|\sqrt{x^2-1}}\)

同理可得\(\csc^{-1}(x)'=-\frac{1}{|x|\sqrt{x^2-1}}\)

双曲函数的导数

我们只粗略的讲双曲函数，因为他实际上是指数函数的求导，所以十分简单，我们放在最后讲

双曲正弦/余弦函数的导数

\[\sinh(x)'=\Big(\frac{e^x-e^{-x}}{2}\Big)'=\frac{e^x+e^{-x}}{2}=\cosh(x)\\ \cosh(x)'=\Big(\frac{e^x+e^{-x}}{2}\Big)'=\frac{e^x-e^{-x}}{2}=\sin(x) \]

其它双曲函数的导数

和三角函数一样的，我们可以通过\(\sinh\)和\(\cosh\)来定义其它双曲函数，结论如下，你可以自己推出来。

\[\tanh(x)'=\frac{1}{\cos^2(x)}，\coth(x)=-\frac{1}{\sinh^2(x)} \]