区间dp

acwing 282.石子合并

https://www.acwing.com/problem/content/284/

①因为我们枚举的划分线是左边部分包含该划分点，所以划分点$k$是可以等于$i$的，但是不包含$j$，所以划分点$k$不能等于$j$。

②为了使在计算当前状态的时候，所需要的状态已经都计算出了，所以我们要以区间的长度进行枚举(枚举区间长度应从$2$开始枚举，因为区间长度是$1$的时候，合并没有代价)。

③因为合并的代价都是区间的和与区间的和相加，而每一次求区间和的复杂度太高，所以我们需要预先处理一个前缀和数组$s$。

代码：$O(n^3)$

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 310;
int f[N][N];
int s[N];
int n;

int main(){
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)cin >> s[i], s[i] += s[i - 1];
    
    for(int len = 2 ; len <= n ; len ++)
        for(int i = 1 ; i + len - 1 <= n ; i ++)
        {
            int l = i, r = i + len - 1;
            f[l][r] = 1e8;
            for(int k = l ; k < r ; k ++)
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
        }
    
    cout << f[1][n] << endl;
    return 0;
}

 

acwing 1068.环形石子合并

https://www.acwing.com/problem/content/1070/

题意：在石子合并的基础上，改成环形的形式（将首尾相连，首和尾算相邻）。

核心：将环转换为区间。

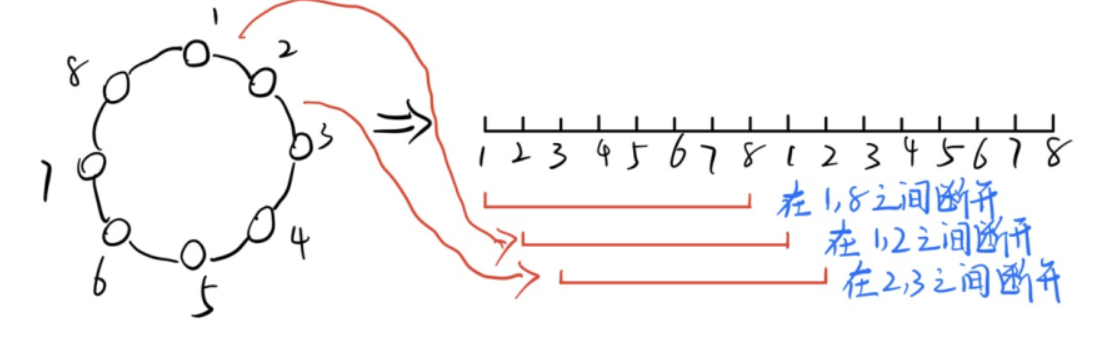
朴素的想法是：将每两个点相邻关系看做是有一条边，枚举每一条边，“砍断”这条边，得到一条线性的石子合并问题求解。这样的时间复杂度就是$O(n^4)$，会超时。

优化：将两条一样的区间相连。这样，得到长度为$2n$的区间上，包含了所有$n$的区间。时间复杂度$O((2n)^3)$。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 410, INF = 0x3f3f3f3f;//开两倍空间
int f[N][N], g[N][N];
int w[N], s[N];
int n;

int main(){
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)
    {
        cin >> w[i];
        w[i + n] = w[i];
    }
    for(int i = 1 ; i <= 2 * n ; i ++)s[i] = s[i - 1] + w[i];
    
    memset(f, 0x3f, sizeof f);
    memset(g, -0x3f, sizeof g);
    
    for(int len = 1 ; len <= n ; len ++)
        for(int l = 1 ; l + len - 1 <= 2 * n ; l ++)
        {
            int r = l + len - 1;
            if(len == 1)f[l][r] = g[l][r] = 0;//代价为0
            for(int k = l ; k < r ; k ++)
            {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
                g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
            }
        }
    
    
    int minv = INF, maxv = -INF;
    for(int i = 1 ; i <= n ; i ++)
    {
        minv = min(minv, f[i][i + n - 1]);
        maxv = max(maxv, g[i][i + n - 1]);
    }
    
    cout << minv << endl;
    cout << maxv << endl;
    return 0;
}

 

acwing 320.能量项链

https://www.acwing.com/problem/content/322/

本题的形式是二维的$(2, 4)(4, 5)(5, 7)(7, 9)$,可以将其转成一维表示$(2, 4, 5, 7, 9)$，这样$(2, 4)$是一个矩阵，$(4, 5)$是一个矩阵，有三个数，所以区间长度要从$3$开始枚举。并且划分的依据$k$是从$l + 1$到$r - 1$的（左边至少要有一个矩阵或者右边至少要有一个矩阵）。

所以该题与前面不同的是，该题是以点作为相邻的依据，断开的也是点。环形石子合并是以边为相邻依据，断开的是边。

这样得到状态转移方程是:$f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r])$

#include <iostream>

using namespace std;

const int N = 210;

int w[N],f[N][N];

int main(){
    int n ;
    cin>>n;
    //展开两条链
    for(int i = 1; i <= n ; i ++)
    {
        cin >> w[i];
        w[i + n] = w[i];
    }
    
    for(int len = 3; len <= n + 1 ; len ++)//区间从3开始才有代价合并,并且长度是n + 1
    //因为n个区间有n + 1个点，并且该题以点为划分依据
        for(int l = 1 ; l + len - 1 <= 2 * n; l ++)
        {
            int r = l + len - 1;
            for(int k = l + 1 ; k < r; k ++)//枚举分界线是从l + 1 到 r - 1
                f[l][r] = max(f[l][r], f[l][k] + f[k][r] + w[l] * w[k] * w[r]);
        }
    //遍历长度为n + 1的区间
    int res = 0;
    for(int i = 1 ; i <= n ; i ++)res = max(res, f[i][i + n]);
    cout << res << endl;
    return 0;
}

 

 

acwing 1069.凸多边形的划分

https://www.acwing.com/problem/content/1071/

这题的状态转移方程和能量项链是一样的。但有些不同。

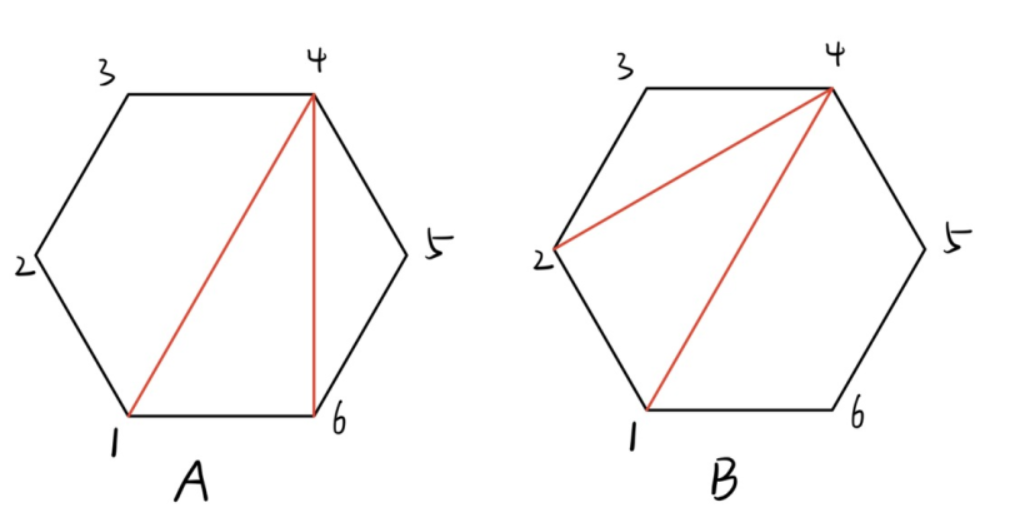
 ①这题以红色三角形的底边作为划分依据，将多边形划分为左边，红色三角形和右边三个部分，每个部分互不相关。其实就是以红色三角形作为分界线一样的区间$dp$。

需要注意的是，虽然是以边为划分，且是一个环，但实质上并不是一个环形的$dp$。例如$A$图中以$(1, 6)$划分，$B$图中以$(2, 1)$划分，实质上$A$图中的所有情况是包含$B$图中的，同理$B$图中的所有情况也是包含$A$图中的情况的，所以以边划分并不是多出了$n$倍的情况，他们实质都是同一种情况。所以这是一个区间长度为$n$的区间$dp$问题（能量项链是$2n$的环形区间$dp$）。

②分界点$k$的枚举依旧是$(l+1, r - 1)$，例如，当$(1, 6)$为底的时候，$k$必须是$(2, 5)$中的数字才能组成一个三角形。所以区间长度也应该从$3$开始枚举。

③另外该题的数据最大是$10^9$规模，单一存储不会爆$int$，但是三个数相乘会爆$long \ long$， 所以是要写高精度的。

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

typedef long long LL;

const int N = 51, M = 28;

LL f[N][N][M];
int w[N];
int n;

void add(LL a[], LL b[])
{
    static LL c[M];
    memset(c, 0, sizeof c);
    for(int i = 0, t = 0; i < M ; i ++)
    {
        t += a[i] + b[i];
        c[i] = t % 10;
        t /= 10;
    }
    memcpy(a, c, sizeof c);
}

void mul(LL a[], LL b)
{
    static LL c[M];
    memset(c, 0, sizeof c);
    LL t = 0;
    for (int i = 0; i < M; i ++ )
    {
        t += a[i] * b;
        c[i] = t % 10;
        t /= 10;
    }
    memcpy(a, c, sizeof c);
}

int cmp(LL a[], LL b[])
{
    for (int i = M - 1; i >= 0; i -- )
        if (a[i] > b[i]) return 1;
        else if (a[i] < b[i]) return -1;
    return 0;
}

void print(LL a[])
{
    int k = M - 1;
    while (k && !a[k]) k -- ;//删除前导零
    while (k >= 0) cout << a[k -- ];
    cout << endl;
}

int main(){
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)cin >> w[i];
    
    LL temp[M];
    for(int len = 3 ; len <= n ; len ++)
        for(int l = 1 ; l + len - 1 <= n ; l ++)
        {
            int r = l + len - 1;
            f[l][r][M - 1] = 9;//置为无穷
            for (int k = l + 1; k < r; k ++ )
            {
                memset(temp, 0, sizeof temp);//注意清空
                temp[0] = w[l];
                mul(temp, w[k]);
                mul(temp, w[r]);
                add(temp, f[l][k]);
                add(temp, f[k][r]);
                if (cmp(f[l][r], temp) > 0)
                    memcpy(f[l][r], temp, sizeof temp);
            }
        }
    print(f[1][n]);
    return 0;
}

 

 

acwing 479.加分二叉树

https://www.acwing.com/problem/content/481/

 

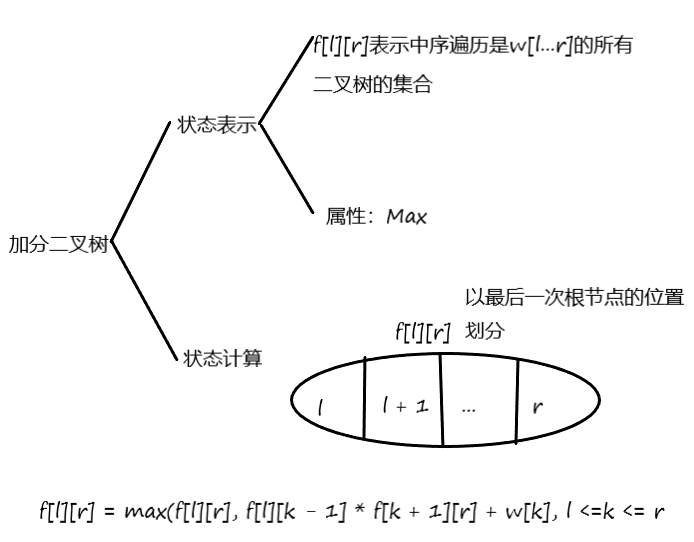
 再用一个$path$数组存储一下改区间的根节点，用$dfs$跑一遍。输出前序遍历。

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 31;
int f[N][N], path[N][N];
int w[N];
int n;

void dfs(int l, int r)
{
    if(l > r)return;
    int k = path[l][r]; 
    cout << k << " ";
    dfs(l, k - 1);
    dfs(k + 1, r);
}

int main(){
    cin >> n;
    for(int i = 1 ; i <= n ; i ++)cin >> w[i];
    
    for(int len = 1 ; len <= n ; len ++)
        for(int l = 1 ; l + len - 1 <= n ; l ++)
        {
            int r = l + len - 1;
            for(int k = l ; k <= r ; k ++)
            {
                int left = k == l ? 1 : f[l][k - 1];
                int right = k == r ? 1 : f[k + 1][r];
                int score = left * right + w[k];
                if(l == r)score = w[r];
                if(f[l][r] < score)
                {
                    f[l][r] = score;
                    path[l][r] = k;
                }
            }
        }
        
    cout << f[1][n] << endl;
    dfs(1, n);
    return 0;
}

 

 

acwing 321.棋盘分割

https://www.acwing.com/problem/content/323/

 二维前缀和+记忆化搜索

$\frac{1}{n}(\sum_{i=1}^{n}(x_i-\bar{x}))=\frac{1}{n}(\sum_{i=1}^{n}((x_i)^2 - 2\bar{x}\sum_{i = 1}^{n}x_i+n(\bar{x})^2 ))=\frac{1}{n}(\sum_{i=1}^{n}((x_i)^2 -n(\bar{x})^2 ))$

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>

using namespace std;

const int N = 16;
const double INF = 1e9;
double f[N][N][N][N][N], s[N][N];
int n;
double X;

double get(int x1, int y1, int x2, int y2)
{
    double sum = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] - X;
    return sum * sum / n;
}

double dp(int x1, int y1, int x2, int y2, int k)
{
    double &v = f[x1][y1][x2][y2][k];
    if(v >= 0)return v;
    if(k == 1)return v = get(x1, y1, x2, y2);
    
    v = INF;
    for(int i = x1 ; i < x2 ; i ++)//按行切
    {
        v = min(v, dp(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));
        v = min(v, dp(i + 1, y1, x2, y2, k - 1) + get(x1, y1, i, y2));
    }
    for(int i = y1 ; i < y2 ; i ++)//按列切
    {
        v = min(v, dp(x1, y1, x2, i, k - 1) + get(x1, i + 1, x2, y2));
        v = min(v, dp(x1, i + 1, x2, y2, k - 1) + get(x1, y1, x2, i));
    }
    return v;
}

int main(){
    cin >> n;
    for(int i = 1 ; i <= 8 ; i ++)
        for(int j = 1 ; j <= 8 ; j ++)
        {
            cin >> s[i][j];
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    
    memset(f, -1, sizeof f);
    X = (double)s[8][8] / n;//浮点数除法
    printf("%.3lf\n", sqrt(dp(1, 1, 8, 8, n)));
    return 0;
}